Лабораторная работа №3
ЦЕЛЬ РАБОТЫ: Изучение понятий внешних сил, момента импульса, момента инерции, закона динамики вращательного движения твердого тела, экспериментальное исследование закономерностей гироскопического эффекта, опытное определение полного момента инерции гироскопа.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: гироскоп.
КРАТКАЯ ТЕОРИЯ
Гироскопом называют массивное однородное твёрдое тело, вращающееся с большой угловой скоростью вокруг свободной оси, совпадающей с главной осью симметрии (ротор). Гироскоп называют уравновешенным (или свободным), если его центр масс остаётся неподвижным при любых изменениях ориентации его оси в пространстве (основным свойством свободного гироскопа является его способность сохранять неизменным направление оси ротора). Иначе говоря, центр масс совпадает с точкой опоры. Такой гироскоп называют гироскопом с одной закрепленной точкой.
Рассмотрим гироскоп с закрепленным центром масс (рис.1), Движение гироскопа описывается уравнением моментов (основного закона динамики вращательного движения):
(1)
где 
- момент импульса гироскопа, 
- результирующий момент внешних сил, приложенных к нему.
В случае свободного гироскопа, когда 
, ось гироскопа сохраняет свою ориентацию в пространстве и вращается с постоянной угловой скоростью 
, поэтому момент импульса = const.
,
где 
- момент инерции гироскопа относительно оси собственного вращения.
Если к оси гироскопа приложить внешнюю силу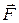 
, например, переместить груз массы 
из положения равновесия в ту или иную сторону, как показано на рисунке, возникает момент силы , лежащий в горизонтальной плоскости и перпендикулярный вектору . В соответствии с уравнением (1) вектор 
совпадает по направлению с вектором , то есть вектор приращения момента импульса перпендикулярен моменту импульса гироскопа . В результате действия силы будет происходить изменение ориентации оси гироскопа в горизонтальной плоскости. Угол поворота вектора момента импульса можно вычислить по формуле:
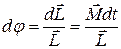(2)
Модуль угловой скорости вращения оси (прецессии) гироскопа:
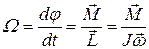(3)
Взаимная ориентация векторов , и 
определяется векторным произведением:
(4)
Поскольку вектор поворачивается вместе с , и их взаимное расположение не меняется со временем, то под действием постоянной по модулю силы 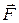, ось гироскопа будет вращаться с постоянной угловой скоростью . Такое движение называют прецессией, - угловая скорость прецессии. Все приведённые рассуждения справедливы для быстровращающегося гироскопа, то есть при >> 
или >> .
