Конкретные математические теории, развиваемые в рамках представлений конструктивной математики, обладают рядом существенных отличий от соответствующих теоретико-множественных теорий.
Например, основное понятие математического анализа — понятие вещественного числа — вводится в традиционном варианте теории на базе общего представления о множестве. Для конструктивной математики, требующей, чтобы рассмотрение ограничивалось конструктивными объектами, такой способ определения понятия вещественного числа неприемлем. В ней под вещественными числами обычно понимают записи алгоритмов 
, перерабатывающих любое натуральное число в некоторое рациональное число, и удовлетворяющих условию
Такие записи представляют собой конструктивные объекты и допускаются к рассмотрению в конструктивной математике. Как обычно, два вещественных числа и 
считаются равными, если выполняется условие
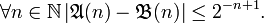
Следует отметить, что проблема распознавания равенства двух произвольных вещественных чисел является алгоритмически неразрешимой, а потому при конструктивном понимании математических суждений утверждение
«любые два вещественных числа или равны, или не равны»
оказывается ложным. Соответственно, теоретико-множественное представление об атомарности континуума (его составленности из чётко отделённых друг от друга точек) не переносится в конструктивную математику.
Многие утверждения теоретико-множественного анализа в конструктивном анализе опровергаются на примерах. Таковы, в частности, теорема о сходимости монотонной ограниченной последовательности и лемма Гейне-Бореля о выборе покрытия. Ряд других утверждений теоретико-множественного анализа могут быть перенесены в конструктивную математику лишь при условии понимания «существования» искомого объекта как квазиосуществимости (а не потенциальной осуществимости). Таковы теорема о представлении вещественных чисел систематическими дробями и теорема о нуле знакопеременной непрерывной функции.
С другой стороны, в конструктивном анализе доказывается ряд утверждений, не имеющих теоретико-множественных аналогов. Одним из наиболее ярких примеров здесь является теорема Г. С. Цейтина о непрерывности любого отображения из сепарабельного метрического пространства в метрическое пространство. Из этой теоремы следует, в частности, что любое отображение метрических пространств является непрерывным по Гейне. Следует заметить, что известны примеры отображений из несепарабельных пространств, которые не являются непрерывными по Коши. Таким образом, в конструктивной математике может быть опровергнуто на примерах утверждение об эквивалентности непрерывности отображения по Коши и по Гейне, доказываемое в классическом анализе на основе привлечения сильных теоретико-множественных средств (в частности, аксиомы выбора).
Литература
· А. А. Марков. Избранные труды. Т. II. Теория алгорифмов и конструктивная математика, математическая логика, информатика и смежные вопросы. — М.: Изд-во МЦНМО, 2003.
· А. А. Марков, Н. М. Нагорный. Теория алгорифмов, изд. 2. — М.: ФАЗИС, 1996.
· Н.М.Нагорный, Абстракция актуальной бесконечности, Абстракция отождествления, Абстракция потенциальной осуществимости, Математическая энциклопедия, М.: "Советская энциклопедия", 1977, т.1, с. 43, 44.
· Б. А. Кушнер. Лекции по конструктивному математическому анализу. — М.: Наука, 1973.
· Б.А.Кушнер, Конструктивная математика, Математическая энциклопедия, М.: "Советская энциклопедия", 1979, т.2, с. 1042.
· Н.И.Кондаков, Логический словарь-справочник, М.: "Наука", 1975, с. 259.
· Г.И.Рузавин, О природе математического знания, М., 1968.
· О.Е.Акимов, Дискретная математика: логика, группы, графы, Изд. 2, М.: "Лаборатория Базовых Знаний", 2003. (Вся книга и особо глава "Конструктивизм", с. 317)
