Для представления вещественных чисел в современных компьютерах принят способ представления с плавающей запятой. Этот способ представления опирается на нормализованную (экспоненциальную) запись действительных чисел.
Как и для целых чисел, при представлении действительных чисел в компьютере чаще всего используется двоичная система, следовательно, предварительно десятичное число должно быть переведено двоичную систему.
Нормализованная запись числа.
Нормализованная запись отличного от нуля действительного числа - это запись вида a= 
m*Pq, где q - целое число (положительное, отрицательное или ноль), а m - правильная P-ичная дробь, у которой первая цифра после запятой не равна нулю, то есть 
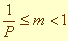. При этом m называется мантиссой числа, q - порядком числа.
Примеры:
1. 3,1415926 = 0, 31415926 * 101;
2. 1000=0,1 * 104;
3. 0,123456789 = 0,123456789 * 100;
4. 0,00001078 = 0,1078 * 8-4; (порядок записан в 10-й системе)
5. 1000,00012 = 0, 100000012 * 24.
Так как число ноль не может быть записано в нормализованной форме в том виде, в каком она была определена, то считаем, что нормализованная запись нуля в 10-й системе будет такой:
0 = 0,0 * 100.
Нормализованная экспоненциальная запись числа - это запись вида a= m*Pq, где q - целое число (положительное, отрицательное или ноль), а m - P-ичная дробь, у которой целая часть состоит из одной цифры. При этом (m-целая часть) называется мантиссой числа, q - порядком числа.
Представление чисел с плавающей запятой.
При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, был придуман так называемый смещённый порядок, который рассчитывается по формуле 2a-1+ИП, где a - количество разрядов, отводимых под порядок.
Пример:
Если истинный порядок равен -5, тогда смещённый порядок для 4-байтового числа будет равен 127-5=122.
Алгоритм представления числа с плавающей запятой.
1. Перевести число из p-ичной системы счисления в двоичную;
2. представить двоичное число в нормализованной экспоненциальной форме;
3. рассчитать смещённый порядок числа;
4. разместить знак, порядок и мантиссу в соответствующие разряды сетки.
Пример:
Представить число -25,625 в машинном виде с использованием 4 байтового представления (где 1 бит отводится под знак числа, 8 бит - под смещённый порядок, остальные биты - под мантиссу).
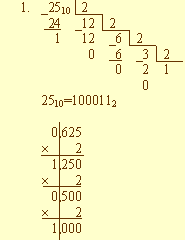
2510=1000112
0,62510=0,1012
-25,62510= -100011,1012
2. -100011,1012 = -1,000111012 * 24
3. СП=127+4=131
4.
Можно заметить, что представление действительного числа не очень удобно изображать в двоичной системе, поэтому часто используют шестнадцатеричное представление:
Окончательный ответ: C1CD0000.
