Основы физики твердых тел
Симметрии твердых тел
Твердые тела. Наиболее характерной особенностью твердых тел, отличающих их, как агрегатное состояние вещества от других агрегатных состояний, является сохранение формы и объема. Благодаря этому твердые тела сыграли главную роль при формировании в сознании человека понятий пространства, геометрических образов и соотношений между ними, а также в развитии теории измерения пространства. Движение твердых тел явилось той основой, на которой были выработаны понятия о механическом движении и перемещении материальных объектов.
Место, занимаемое материальным телом, и его форма абстрагируются в нашем понятии в виде самостоятельных геометрических пространственных образов. Благодаря этому приобретает смысл представление о сравнении твердых тел по их форме, размеру и т.д.
Очень важным геометрическим свойством твердых тел является их симметрия. Например, найденный на дороге камень отличается от кирпича в первую очередь тем, что он имеет неправильную форму. Слова «правильная» и «неправильная» форма являются субъективным отражением объективных свойств форм материальных тел, а именно их симметрии.
Мы говорим, что прямой цилиндр более симметричен, чем прямоугольный параллелепипед, а шар более симметричен, чем цилиндр. Мы говорим также, что внешняя форма человеческого тела, я также тела большинства животных симметричны. Задача состоит в том, чтобы дать математическую формулировку понятию симметрии.
Определение симметрии. Под симметрией понимается способность твердого тела совмещаться с самим собой в результате его движения или воображаемых операций над его точками. Чем большим числом способов такое совмещение возможно, тем более симметричной является форма тела.
Например, прямой круглый цилиндр совмещается с самим собой при повороте вокруг своей оси на любой угол. Он также совмещается с самим собой при повороте на угол в 180° вокруг любой оси, перпендикулярной оси цилиндра, проведенной через точку оси на половине высоты цилиндра. Если же взять шар, то он может быть совмещен с самим собой при повороте его на любой угол вокруг любой оси, проходящей через центр шара. Ясно, что возможностей для совмещения шара с самим собой значительно больше, чем для цилиндра. Именно этот факт выражается в утверждении, что шар является телом более симметричным, чем прямой круглый цилиндр.
Однако к совмещениям тела с самим собой только с помощью пространственных движений симметрия не сводится. Например, левая половина человеческого тела никакими пространственными движениями не может быть совмещена с правой. Другими словами, на левую руку нельзя надеть правую перчатку. Под симметрией левой и правой рук понимают не возможность совмещения левой руки с правой в результате пространственного совмещения, а возможность совмещения правой руки с отражением левой руки в плоском зеркале.
Несмотря на кажущееся чрезвычайно большое многообразие возможностей симметрии твердых тел, все они складываются из четырех элементов. Различные комбинации этих четырех элементов симметрии и составляют всевозможные симметрии твердых тел.
Ось симметрии п- го порядка. Если тело совмещается само c собой при повороте вокруг некоторой оси на угол 2p¤ п, то эта ось называется осью симметрии п-го порядка. Например, квадратный цилиндр (рис. 4.1) совмещается с самим собой при повороте на угол p/2 вокруг оси, проходящей через точки пересечения диагоналей квадратов, образующих его основание. Следовательно, эта ось является только осью 4-го порядка. Нет необходимости доказывать, что любая ось тела является осью 1-го порядка.
Плоскость симметрии. Если тело совмещается само с собой в результате зеркального отражения его точек в некоторой плоскости, то эта плоскость называется плоскостью симметрии тела. На рис. 4.2 заштрихованная поверхность – плоскость симметрии.
Рис. 4.2
Центр симметрии. Если тело совмещается с самим собой при инверсии относительно некоторой точки, то эти точки называются центром симметрии (т. О на рис. 4.1).
Точечные группы симметрии. Совокупность элементов симметрии тела называется его группой симметрии. Рассмотренные элементы симметрии характерны тем, что они оставляют неподвижной по крайней мере одну точку тела. Соответствующие им группы симметрии называются точечными. Все перечисленные симметрии можно описать с помощью одних только отражений в плоскости. Поворот на угол a можно представить в виде двух последовательных отражений в плоскостях, пересекающихся на оси поворота под углом a/2 (рис.4.3). Инверсия относительно центра симметрии сводится к трем отражениям в трех взаимно перпендикулярных плоскостях, проходящих через центр симметрии.
Рис. 4.3
Зеркальные изомеры. Два тела могут быть похожими друг на друга и могут быть совмещены друг с другом с помощью отражения в плоскости, однако, они не могут быть совмещены друг с другом никакими пространственными движениями. В качестве примера укажем на кисти человеческих рук. Такие тела называются зеркальными изомерами. Известны многие молекулы, являющиеся зеркальными изомерами. Они отличаются по своим свойствам в том же смысле, в каком правое отличается от левого. Например, они в разных направлениях вращают плоскость поляризации света, проходящую через них, если только такое вращение вообще имеет место. Химические реакции между одноименными зеркальными изомерами проходят по-другому, чем между разноименными. Например, правый изомер одного вещества с правым изомером другого реагирует иначе, чем правый с левым.
Кристаллические решетки
Необходимость периодической структуры. Твердое состояние возникает при столь сильном взаимодействии между молекулами (атомами или ионами), что тепловое движение молекул не играет в структуре столь значительную роль, которую оно играет в жидкостях и особенно в газах. В результате этого молекулы располагаются друг относительно друга в некоторых фиксированных с большой точностью положениях, осуществляя небольшие тепловые колебания около положений равновесия. Взаимное расположение точек равновесия определяется условиями равновесия. Ясно, что если эти условия равновесия выполнены в некоторой области пространства и обусловили взаимное расположение молекул в этой области пространства, то они должны быть выполнены в другой области и, следовательно, должны обусловить аналогичное расположение молекул в другой области пространства. А это означает, что взаимное расположение молекул повторяется при переходе из одних областей пространства в другие, т.е. структура твердых тел периодическая. Она реализуется в виде кристаллической решетки, а сами твердые тела являются кристаллами. Точки равновесия составляющих кристаллы атомов, молекул или ионов называются узлами кристаллической решётки.
Однако, при такой аргументации возникает вопрос о причинах существования аморфных твёрдых тел, таких, как стекло, пластик, и аналогичных веществ без периодической структуры. Ответ состоит в том, что они не находятся в равновесном состоянии и с течением времени изменяют свою структуру, приближаясь к кристаллическому состоянию. Например, стекло по истечении нескольких сотен лет кристаллизуется. Процесс его кристаллизации может быть значительно ускорен при повышенной температуре, когда оно размягчается. В пластиках процесс кристаллизации сильно затруднён перепутыванием между собой образующих их длинных молекул. Для повышения качества пластиков специальной обработкой добываются того, чтобы практически все молекулы стали различными (физические длины, боковые цепи и т.д.), и для обеспечения стабильности нет необходимости иметь периодическую структуру.
Примитивная решетка. В результате периодичности структуры кристаллической решетки должна существовать некоторая элементарная совокупность атомов, повторением которой во всех направлениях можно исчерпать всю не ограниченную в пространстве решетку. Как элементарная совокупность атомов (для простоты выражений мы говорим об атомах, хотя это могут быть и молекулы, ионы), так и порождаемая её повторением решетка, являются, вообще говоря, очень сложными образованиями. Поэтому всю решетку целесообразно разбить на некоторые, более простые подрешетки, каждая из которых была бы достаточно простой. Ясно, что эта подрешетка сама является решеткой. Наиболее простой решеткой является решетка, состоящая из параллелепипедов как элементарной совокупности атомов, повторением которой исчерпывается вся решетка (рис. 4.4 ).
Выбрав начало координат в некотором узле такой решетки, можно радиус-вектор любого другого узла представить в виде
, (4.1)
где n1, n2, n3 – целые числа (включая нуль). Векторы 
называются базисными, а их совокупность – базисом решетки. Длины ребер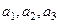 
называются основными периодами решетки. Параллелепипед с ребрами 
вместе с атомами в его вершинах называется элементарной ячейкой кристаллической решетки. Если в формуле (4.1) числа n1, n2, n3 пробегают всевозможные независимые целочисленные значения от -¥ до +¥, то радиус-вектор r проходит все узлы решетки и нет никаких узлов решетки, которые не охватывались бы формулой (4.1). Такая решетка называется примитивной или решеткой Браве, а её элементарная ячейка – примитивной ячейкой.
Конкретная кристаллическая решетка, вообще говоря, не может быть представлена в виде одной решетки Браве, а является совокупностью нескольких решеток Браве. Поэтому она называется сложной.
Неоднозначность выбора базиса примитивной решетки. Выбор базиса даже примитивной решетки не является однозначным. В этом легко убедиться по рис. 4.5, где для двумерного случая параллельными пунктирными линиями показаны два возможных построения примитивной решетки с различными базисами. В первом случае базис составлен векторами 
и 
, во втором – векторами 
, 
. Элементарная ячейка в первом случае является прямоугольным параллелограммом, во втором – непрямоугольным. Около каждого атома в узле решетки в плоском случае располагаются четыре элементарных ячейки. Следовательно, площадь, занимаемая одним атомом в решетке, равная общей площади, деленной на число атомов, равна площади элементарной ячейки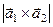 
в первом случае и 
- во втором.
Как и следовало ожидать, площади элементарных ячеек в обоих случаях равны, хотя базисы различны. Все эти выводы без труда переносятся на трехмерный случай, в котором выбор элементарной кристаллической ячейки также неоднозначен, однако, объем элементарной ячейки при всевозможных выборах базиса является неизменным и по форме для объема параллелепипеда равным
. (4.2)
Это есть объем, приходящийся в решетке на один атом.
Различные примитивные базисы отличаются друг от друга длиной базисных векторов или, что то же самое, основными периодами решетки. Примитивная решетка с минимальными периодами называется приведенной.
Определить, является некоторая заданная решетка примитивной или сложной, не всегда легко с первого взгляда. Лучше всего это делать, рассматривая всю решетку, а не её небольшую часть, равную элементарной ячейке. Задача сводится к возможности проведения трех систем параллельных плоскостей таким образом, чтобы все атомы решетки оказались в точках пересечения плоскостей и не было бы атомов, не попавших в эти точки пересечения плоскостей.
Рассмотрим в качестве примера плоскую решетку (рис. 4.6). Если в качестве базисных взять векторы 
, 
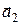, то решетка представляется сложной, поскольку атомы, находящиеся в центрах квадратов, не попадают в узлы примитивной решетки, построенной на этом базисе.
На первый взгляд, кажется, что для учета этих узлов необходима ещё одна примитивная решетка, и, следовательно, исходная решетка является сложной, а не примитивной. Однако такое заключение неправильно. Возьмем в качестве базисных векторы a¢1 и a¢2. В этом базисе вся исходная решетка может быть представлена в виде одной примитивной решетки, т.е. исходная решетка тоже является примитивной. Это очевидно, если посмотреть на систему пунктирных линий (рис. 4.3).
Трансляционная система. Ввиду бесконечной протяженности решетка обладает кроме симметрий, характерных для твердых тел, трансляционной симметрией, т.е. способностью совмещаться с собой в результате поступательного перемещения. Например, если примитивную решетку переместить вдоль одного из ребер элементарной ячейки на целое число основных периодов, то решетка совпадёт или совместится с собой. Если сместить решетку на вектор r, определенный в (4.1), то решетка опять совпадёт с собой. Поэтому вектор r называется вектором трансляции. Пользуясь этой терминологией, можно сказать, что вся примитивная решетка может быть получена из любого узла, если его подвергнуть всевозможным трансляциям параллельно базисным векторам.
Пространственные группы. Элементы симметрии твердого тела образуют точечные группы симметрии. Если к ним добавить трансляционную симметрию, характерную для периодических бесконечных структур, то совокупность этих симметрий образует пространственную группу. Поэтому можно сказать, что кристаллические решетки характеризуются пространственными группами симметрии.
Элементы симметрии решетки. Прежде всего необходимо отметить, что симметрии решетки в целом отличаются от симметрий её элементарной решетки. Это очевидно из того, что элементарная ячейка выбирается неоднозначно, а различные элементарные ячейки могут иметь различную симметрию. Поэтому под симметрией решетки понимается симметрия именно решетки, а не её элементарной ячейки.
Ясно, что всякая примитивная решетка имеет центр симметрии, которым может быть любой узел примитивного параллелепипеда, середина его ребер и центры его граней. Плоскость симметрии также является элементом симметрии решеток. Что же касается осей, то они могут быть лишь осями 2-, 3-, 4- и 6-го периодов, а оси других порядков невозможны. Для доказательства заметим, что при вращении атомы решетки перемещаются в плоскостях, перпендикулярных оси вращения.
Рассмотрим атомы, лежащие в некоторой плоскости. Они создают плоскую кристаллическую решетку, узлы которой образуют систему правильных многоугольников, переходящих при вращении друг в друга и, следовательно, плотно, без промежутков, покрывающих всю поверхность. Рассмотрим точку О (рис. 4.7), в которой сходятся ребра примыкающих в этой точке правильных многоугольников. Если р – число ребер, сходящихся в этой точке, то угол между ребрами равен 2p/ р. С другой стороны, угол между сторонами правильного п -угольника равен p (п–2)/п.
При заполнении плоскости правильными многоугольниками без промежутков эти углы равны:
2 p/ р= p (п–2)/п. (4.3)
Отсюда следует, что
р=2п/(п–2), (4.4)
причем числа р и п должны быть целыми. Решениями этого уравнения в целых числах р и п являются значения
п=3, п=4, п=6. (4.5)
Таким образом, поверхность без промежутков можно покрыть равносторонними треугольниками, квадратами и правильными шестиугольниками (структура пчелиных сот)
Других правильных многоугольников, способных без промежутков покрыть поверхность, не существует. К ним добавляется, очевидно, возможная ось п=2, соответствующая отражению в плоскости, проходящей через ось, а также тривиальная ось п=1, соответствующая углу поворота на 2 p. Таким образом у кристаллической решетки возможны оси вращения только 2-, 3-, 4- и 6-го порядков. Аналогично показывается, что зеркально-поворотные оси могут быть только тех же порядков. В результате получается, что число элементов точечных групп симметрии у кристаллических решеток конечно, а следовательно, конечно и число возможных симметрий.
Кристаллические классы. Поскольку сложная кристаллическая решетка состоит из решеток Браве, то классифицировать кристаллы в первую очередь целесообразно по симметрии решеток Браве, причем под симметрией, как это было только что сказано, понимается точечная симметрия. Такая классификация была произведена Браве. Он сказал, что хотя симметрия решетки не обязательно совпадает с симметрией любой примитивной ячейки, можно всегда найти такую примитивную ячейку, которая имеет те же элементы симметрии, что и решетка в целом. Это возможно для всех решеток, за исключением гексагональных, где примитивная ячейка не содержит всех элементов симметрии, которые имеются у решетки в целом. Наименьшая из примитивных ячеек, включающая в себя все элементы симметрии решетки, называется ячейкой или параллелепипедом Браве.
Имеется шесть типов примитивных параллелепипедов Браве, и поэтому с учетом гексагональной решетки – всего семь типов решеток или семь типов кристаллических систем. Помещение в центрах граней или в центре объёма параллелепипедов Браве новых атомов не изменяет симметрии решетки, но добавляет новые типы решетки. Поэтому всего существует 14 типов решеток Браве, распределенных по семи кристаллическим системам. Подробное описание этих решеток является предметом кристаллографии, а мы здесь ограничимся лишь краткими замечаниями. На рис. 4.9 изображены решетки, принадлежащие семи кристаллическим системам. В каждой из систем, за исключением гексагональной, первым 
показан основной параллелепипед Браве, а затем указаны решетки, которые получаются центрированием объема и граней основного параллелепипеда. Эта операция не изменяет симметрии решетки, но, конечно, примитивные ячейки получаемой в результате этого решетки уже не совпадают с основным параллелепипедом Браве и имеют симметрии, отличные от симметрии решетки. Что касается гексагональной системы, то у неё элементарная ячейка, имеющая те же элементы симметрии, что и решетка, не является параллелепипедом. Элементарный параллелепипед в этом случае указан на рисунке вместе с элементарной ячейкой. На рис. 4.10 даны обозначения осей и углов основного параллелепипеда Браве различных кристаллических систем, характеристика которых дана в табл. 4.1.
Таблица 4.1
Характеристики кристаллических систем
| Кристаллическая система | Соотношение ребер элементарной ячейки | Соотношение между углами в элементарной ячейке |
| Триклинная | a1 ¹ a2 ¹ a3 | a ¹ b ¹ g |
| Моноклинная | a1 ¹ a2 ¹ a3 | a = b = 90° ¹ g |
| Ромбическая | a1 ¹ a2 ¹ a3 | a = b = g = 90° |
| Тетрагональная | a1 = a2 ¹ a3 | a = b = g = 90° |
| Кубическая | a1 = a2 = a3 | a = b = g = 90° |
| Ромбоэдрическая | a1 = a2 = a3 | a = b = g, но < 120° и ¹ 90° |
| Гексагональная | a1 = a2 ¹ a3 | a = b = 90°, g = 120° |
Симметрии сложных решеток. Поскольку сложная решетка слагается из примитивных, имеющих различные симметрии, то симметрия сложной решетки существенно отличается от симметрий слагающих её примитивных решеток. Кроме того, для сложной решетки возможны дополнительные элементы симметрии, а именно: винтовая ось и плоскость зеркального скольжения.
Винтовой осью п -го порядка называется прямая, перемещение решетки вдоль которой с одновременным вращением на угол 2p¤ п приводит к её совпадению с собой. Винтовые оси одного и того же порядка могут отличаться друг от друга направлением вращения, т.е. быть «левыми» или «правыми».
Плоскостью зеркального скольжения называется такая плоскость, при отражении в которой с одновременным смещением на определенное расстояние параллельно плоскости решетка совмещается сама с собой.
Таким образом, наряду с элементами точечной симметрии и трансляционной симметрией решетка обладает другими элементами симметрии - винтовыми осями и плоскостями зеркального скольжения. Совокупность всех элементов симметрии называется её пространственной группой. Как было показано Е.С. Фёдоровым, всего может существовать 230 пространственных групп. Эти группы называются группами Фёдорова или фёдоровскими группами. Не все они обнаружены у кристаллов, имеющихся в природе. Найдены пока кристаллы для 177 фёдоровских групп. Более подробно эти вопросы рассматриваются в курсе кристаллографии.
Кристаллографические системы координат. В качестве систем координат, в которых задается положение атомов решетки, берут прямолинейные системы координат, оси которых совпадают с ребрами параллелепипеда Браве, а начало находится в одном из узлов кристаллической решетки. В качестве единицы длины по каждой оси принимается длина соответствующего ребра параллелепипеда Браве. Поэтому координаты атомов выражаются целыми числами. Такие системы координат называются кристаллографическими. Выбор осей координат дается в табл. 4.1. В кубических, тетрагональных и ромбических кристаллах системы координат являются прямоугольными, остальные – косоугольными. В гексагональных кристаллах за оси X и Y параллелепипеда Браве принимаются стороны основания правильного шестиугольника (см. рис. 4.9), составляющие угол 120°друг с другом, а ось Z направлена перпендикулярно основанию. Выбор параллелепипеда Браве для моноклинных и триклинных кристаллов не однозначен. Условились, что в моноклинных кристаллах за ось Z берется та, которая образует прямой угол с двумя другими осями (см. табл. 4.1).
Обозначение атомных плоскостей. В бесконечном кристалле можно провести бесконечное число плоскостей, в каждой из которых лежит бесконечное число атомов. Для того чтобы характеризовать семейство параллельных плоскостей, достаточно определить одну из них, причем без потери общности можно ограничиться примитивными решетками.
Уравнение любой плоскости в прямолинейных (но не обязательно прямоугольных!) координатах имеет вид:
, (4.6)
где |ΟΑ|, |ОΒ|, |ΟС| - длины отрезков (в осевых единицах), отсекаемых плоскостью на осях координат (рис. 4.11). Если в точке пересечения оси с плоскостью находится атом, то соответствующая из величин А, В, С является целочисленной. Но, вообще говоря, атомная плоскость может пересекаться с осями координат также и в точках, в которых нет атомов. В этом случае соответствующая из величин |ΟΑ|, |ОΒ|, |ΟС| не будет целочисленной. Однако она всегда выражается рациональным числом (положительным или отрицательным). Чтобы в этом убедиться, достаточно заметить, что для атомов, находящихся в рассматриваемой плоскости, величины x, y, z в уравнении (4.6) являются целочисленными. Поэтому, взяв каких-то три конкретных атома в плоскостях, не лежащих на одной прямой, мы из (4.6) получим три линейных уравнения с целочисленными коэффициентами для определения трех неизвестных (1/|ΟΑ|, 1/|ОΒ|, 1/|ΟС|). Ясно, что решение этих уравнений дается рациональными числами, а следовательно, и величины |ΟΑ|, |ОΒ|, |ΟС| являются рациональными числами. Поэтому уравнение (4.6) может быть переписано в виде
, (4.7)
где h, k, l – целые числа, причем можно считать, что они не имеют общего множителя, поскольку в противном случае на этот общий множитель можно было бы сократить все члены уравнения. Целые числа h, k, l однозначно определяют положение плоскости. Они называются миллеровскими числами и записываются в виде последовательности чисел, заключенной в скобки: (h k l). Если индекс отрицательный, то знак минус ставится над соответствующим числом, например, (
).
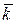
Обозначение направлений. Направление, перпендикулярное плоскости, характеризуемой миллеровскими индексами (h k l), обозначается теми же числами, но заключенными в квадратные скобки [ h k l ].
Дефекты кристаллических решеток
Определение. Дефектами кристаллической решетки называются всякие отклонения от строгой периодичности, которой определяется решетка. Дефекты бывают макроскопическими и микроскопическими. К первым относятся всякого рода трещины, макроскопические пустоты и инородные макроскопические включения в кристаллическую решетку. Вторые обусловлены микроскопическими отклонениями от периодичности. Они бывают точечными и линейными, или дислокациями.
Точечные дефекты. Они бывают трех типов: 1) вакансия, когда в узле решетки отсутствует атом (рис. 4.12); 2) замещение, когда в узле решетки находится атом другого сорта (рис. 4.13); 3) внедрение, когда между узлами, где никаких атомов не должно быть, находится атом (рис. 4.14). Характерной особенностью точечных дефектов является то, что они нарушают лишь ближний порядок в кристаллах, не затрагивая дальнего порядка.
Дислокации. В противоположность точечным линейные дефекты нарушают дальний порядок. Дислокации нарушают правильное чередование атомных плоскостей. Они бывают краевыми и винтовыми.Краевая дислокация сводится к появлению лишней атомной полуплоскости, как бы вдвинутой между атомными плоскостями кристалла (рис. 4.15).
Винтовая дислокация образуется в результате скольжения двух атомных полуплоскостей на один период друг относительно друга, начиная с некоторой линии. На рис. 4.16 показаны атомы решетки в плоскостях, претерпевшие скольжение друг относительно друга. Пунктиром обозначена линия, разграничивающая полуплоскость, испытавшую скольжение, от полуплоскости без скольжения. Дислокации имеют большое значение для механических свойств твердых тел.
Теплоемкость твердых тел
Классическая теория. Моделью является кристаллическое твердое тело, атомы которого колеблются около положений равновесия в узлах кристаллической решетки. Каждый атом может независимо колебаться в трех взаимно перпендикулярных направлениях, являясь относительно этого направления линейным осциллятором. В соответствии с законом о равнораспределении энергии по степеням свободы средняя энергия осциллятора равна kT. Эта энергия состоит из кинетической kT/2 и потенциальной kT/2 энергий.
Таким образом, тело, состоящее из n атомов, вследствие теплового движения обладает энергией
U=3nkT, (4.8)
а теплоемкость этого тела равна
Сv =(dU/dT)v=3nk,(4.9)
т.е. теплоемкость твердого тела является величиной постоянной. Если взять моль молекул вещества, то n является постоянной Авогадро NA, nk = R (где R - молярная газовая постоянная). Формула (4.9) показывает, что молярная теплоемкость равна 3 R и не зависит от температуры. Это закон Дюлонга и Пти. Этот закон утверждает, что молярная теплоемкость всех химических простых твердых тел одинакова и равна 3 R. Этот закон выполняется достаточно хорошо только при сравнительно высоких температурах.
Теплоемкость при низкой температуре. Опыты по измерению теплоемкости при низкой температуре показали, что она зависит от температуры. При приближении температуры к 0 К теплоемкость стремится к нулю по степенному закону Cv ~ T3. Полученная в экспериментах зависимость теплоемкости от температуры изображена на рис. 4.17. Заметим, что такое поведение теплоемкости от температуры наблюдается лишь у неметаллических твердых 
тел, у которых единственной энергией, связанной с тепловым движением, является энергия колебаний атомов в узлах кристаллической решетки. У металлических тел имеются свободные электроны, часть которых также участвует в тепловом движении и дает вклад в теплоемкость. Однако этот вклад невелик, поскольку в тепловом движении участвует лишь небольшая доля электронов, энергии которых лежат вблизи энергии поверхности Ферми. Лишь при низкой температуре, когда вклад в теплоемкость, связанный с движением атомов сильно уменьшается, электронная теплоёмкость становится главной.
Модель Эйнштейна. Чтобы объяснить поведение теплоемкости в зависимости от температуры, А. Эйнштейн в 1907 г. предложил воспользоваться соображениями о дискретном характере энергий, которыми могут обладать осцилляторы, образующие твердое тело, подобно тому, как это было сделано ранее М. Планком для вывода формулы излучения абсолютно черного тела.
Пусть «элементарная» порция энергии, которой может обладать линейный осциллятор, равна ε. Эту энергию можно считать связанной с некоторой частотой колебаний осциллятора таким же соотношением, каким энергия фотона связана с его частотой
ε = 
ω. (4.10)
Вообще говоря, ниоткуда не следует, что минимальная энергия осциллятора равна нулю. Обозначим ее ε0. Для расчета теплоемкости ее точное значение не играет роли. Поэтому возможные энергии, которыми может обладать осциллятор, представляются в виде
εn = ε0 + n ε (n= 0,1,2,…). (4.11)
Естественно предположить, что вероятность Pn состояния осциллятора с энергией ε n задается формулой Больцмана. Поэтому можно написать
Pn=A exp[ - ε n /(kT)] =A exp[-(ε 0+n ε)/(kT)], (4.12)
где А – нормированная постоянная, определяемая условием нормировки вероятности
. (4.13)
Теперь можно вычислить среднюю энергию осциллятора
. (4.14)
По формуле для геометрической прогрессии
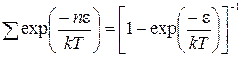. (4.15)
Дифференцируя обе части этого равенства по ε, получаем
. (4.16)
Следовательно, выражение (4.14) принимает вид:
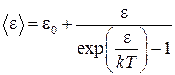. (4.17)
(Примечание: Движение совокупности связанных между собой осцилляторов описывается посредством учета нормальных мод колебаний системы, которые далее будут рассмотрены подробно). Носителем энергии при этом является не отдельный осциллятор, а нормальная мода колебаний системы в целом, которая рассматривается как квазичастица, называемая фононом.
Фононы и другие квазичастицы, являющиеся нормальными модами соответствующих возбуждений (магноны, поляритоны, экситоны и т.д.), не являются частицами в том же смысле, в каком являются частицами фотоны, хотя математические схемы описания их поведения могут иметь много общего.)
Отсюда для энергии колебаний одного моля осцилляторов получаем
. (4.18)
Тогда теплоемкость при постоянном объеме
. (4.19 а)
Это формула Эйнштейна для теплоемкости. В качественном смысле поведение теплоемкости в зависимости от температуры по этой формуле согласуется с экспериментами, результаты которых представлены на рис. 4.17. Действительно, из формулы (4.19 а) видно, что при достаточно большой температуре, 
а при 
получаем
Температура Эйнштейна. «Элементарная порция энергии» ε зависит от свойств вещества твердого тела, причем с увеличением «жесткости» вещества эта величина возрастает, поскольку увеличивается частота ω колебаний в формуле (4.10). Эту энергию принято характеризовать посредствам температуры Эйнштейна (Θ э), определяемой соотношением
k Θ э = ε. (4.19 б)
Формула (4.1 а) может быть переписана:
. (4.19 в)
Недостаточность теории Эйнштейна. Однако в количественном отношении формула (4.19 а) не согласуется с экспериментом, потому что она предсказывает экспоненциальное уменьшение теплоемкости CV ~ exp[-ε/(kT)] при приближении к 0 К, а эксперимент дает лишь степенное уменьшение
CV ~ T 3.
Таким образом, модель Эйнштейна для расчета теплоемкости не точна и должна быть существенно усовершенствована. Наряду с указанным выше количественным несогласием результатов этой теории с экспериментом следует отметить ее другой недостаток, имеющий принципиальный характер. Считается, что твердое тело есть совокупность независимых линейных осцилляторов, энергии которых задаются формулой (4.11), т.е. движения атомов в твердом теле считаются столь же независимыми друг от друга, как движения атомов и молекул в газах. Но это заведомо неправильно, поскольку само удержание атомов около некоторых положений равновесия есть результат взаимодействия атомов между собой. Поэтому в твердом теле нельзя рассматривать атомы как независимые, необходимо принять во внимание их коллективные взаимодействия. Именно учет этого взаимодействия атомов приводит к теории теплоемкости, согласующейся с экспериментом.
Элементарные возбуждения. Система атомов, составляющих твердое тело, при 0 К находится в основном состоянии с минимальной энергией. Чтобы проанализировать теплоемкость вблизи 0 К, необходимо найти те энергии, которые может иметь система атомов вблизи 0 К. Предположим, что некоторый атом в результате сообщения ему энергии извне движется из положения равновесия в некотором направлении. Сила, стремящаяся вернуть его в положение равновесия, есть просто сила отталкивания со стороны других атомов решетки. Поэтому, выходя из положения равновесия, атом действует с определенными силами на соседние атомы, которые в свою очередь должны покинуть свои положения равновесия, в результате чего движения атомов приобретают коллективный характер. Такое коллективное движение атомов, когда смещение одного атома передается соседнему, затем следующему соседнему и т.д., есть не что иное, как звуковая волна в твердом теле. Таким образом, элементарными возбуждениями являются звуковые колебания.
Нормальные моды. С учетом только что описанного взаимодействия система атомов должна рассматриваться как совокупность связанных осцилляторов. В этом случае любое движение системы атомов может быть представлено как суперпозиция нормальных колебаний или нормальных мод системы. Каждая из нормальных мод кроме прочего характеризуется своей частотой, а энергия этой моды задается формулой (4.10), т.е. мода частоты ω i имеет энергию
εi = ωi, (4.20)
где постоянная для всех мод энергия ε0 отброшена. В данном твердом теле может быть возбуждено одно, два колебания (и больше) данной моды. Если возбуждено n колебаний данной моды, то полная энергия этих n колебаний, очевидно, равна
εin = n ωi. (4.21)
Вероятность того, что с данной модой связана полная энергия ε in, считается подчиняющейся распределению Больцмана и, следовательно,
Pn = A exp[-ε in /(kT)] = A exp[ n ωi/(kT)], (4.22)
где А – нормировочный множитель. Эта формула аналогична (4.12). С ее помощью можно вычислить среднюю энергию, приходящуюся на рассматриваемую моду, а разделив эту энергию на энергию одного колебания моды, можно сразу же получить среднее число <ni> колебаний данной моды, которые возбуждены. Вычисления совершенно аналогичны в математическом смысле, которые привели от формулы (4.12) к формуле (4.17), и дают следующий результат:
. (4.23)
Теперь вопрос вычисления полной энергии возбуждения свелся к нахождению частот нормальных мод и их числа.
Фононы. Выражение (4.20) для энергии, связанной с модой колебаний частоты ω i, по аналогии с соответствующей формулой для энергии фотонов, наводит на мысль рассматривать такую моду, как квазичастицу. Это представление было, в сущности, уже использовано, когда в (4.22) формула Больцмана была применена для определения средней энергии в моде. Такая квазичастица, связанная с модами звуковых колебаний, называется фононом. Введение понятия фононов является плодотворным приемом, значительно облегчающим рассуждения. Оно также весьма эффективно с чисто математической точки зрения, так как формальные математические приемы вычисления различных величин, связанных с фононами, аналогичны соответствующим вычислениям, относящимся к фотонам. Эта аналогия обуславливается тем, что в обоих случаях мы имеем математически одинаковые волновые процессы. Однако физическая сущность этих процессов совершенно различна. Поэтому из факта существования фотонов как частиц, которые обладают соответствующей энергией, обнаруживаемой экспериментально, и могут существовать изолированно, отнюдь не следует, что и фононы являются частицами с аналогичными свойствами. В современной физике имеется большое число других аналогичных квазичастиц, являющихся нормальными модами соответствующих возбуждений (магноны, поляритоны, экситоны и т. д.). Сказанное выше о фононах справедливо также и относительно этих квазичастиц.
Модель Дебая. В твердом теле возможно распространение продольных и поперечных волн с различными скоростями. Поперечные волны могут иметь два различных направления поляризации. Таким образом, можно говорить просто о длинноволновых модах звуковых волн с тремя различными поляризациями, каждая из которых, вообще говоря, различна и может зависеть от направления распространения волны. Однако для упрощения будем рассматривать случай изотропного твердого тела. Вычисление числа мод для каждой поляризации совершенно одинаково. Теория теплоемкости Дебая основывается на расчете числа мод звуковых колебаний твердого тела. К сказанному выше следует лишь добавить, что речь идет о достаточно длинноволновых модах, поскольку возбуждения вблизи температуры 0 К и частоты колебаний должны соответствовать достаточно малым энергиям, т.е. быть малыми.
Дисперсионное соотношение. Прежде всего выведем волновое уравнение, например, для продольных волн, распространяющихся вдоль оси X (рис. 4.18). Пусть имеется тонкий цилиндр, площадь основания которого S и высота 
Обозначим: 
(x,t) –плотность вещества, а p(x,t) - давление, которое в нем возникает в результате изменения плотности; u(x, t) – скорость колебаний частиц вещества вдоль оси X. Эта скорость не является скоростью распространения волны, а во много сотен раз меньше ее.
Напишем закон сохранения массы в объеме: изменение массы в объеме, отнесенное ко времени: d( S 
) /dt, равно разности масс, вошедших в объем и вышедших из него
(4.24)
где последняя величина разложена в ряд Тейлора и сохранен лишь первый член, линейный по 
Остальные члены можно отбросить, поскольку дальше принимается за бесконечно малую величину. После сокращения обеих частей (4.24) на S получаем уравнение
, (4.25)
называемое уравнением непрерывности.
Сила, которая действует на массу в рассматриваемом объеме, обуславливается разностью давлений p на разные стенки цилиндра. Следовательно, уравнение Ньютона имеет вид:
(4.26)
или
(4.27)
Изменения плотности и давления в среде можно считать малыми:
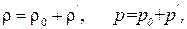(4.28)
где 
и 
- постоянные плотность и давление в среде при отсутствии волны: 
и 
- изменения плотности и давлении, связанные с волной. Обе эти величины являются малыми. Все дальнейшие вычисления проводятся с сохранением величин первого порядка малости по 
и 
.
Подставляя (4.28) в уравнение (4.25) и (4.27) и сохраняя лишь линейные по и члены, получаем:
(4.29)
Этих двух уравнений недостаточно для определения трех неизвестных величин 
и u. Необходимо иметь еще одно уравнение, содержащее эти величины. Им является уравнение состояния, связывающее давление и плотность
p = p (r). (4.30)
Соотношения (4.28) с учетом (4.30) имеют вид:
(4.31)
т.е.
(4.32)
где
(4.33)
Как будет видно из дальнейшего, v является скоростью распространения волн. С помощью (4.32) можно исключить p’ из уравнений (4.29), в результате чего они принимают такой вид:
(4.34)
Продифференцировав первое из уравнений (4.34) по t, а второе – по x, и вычитая первое уравнение из второго, находим
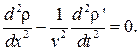(4.35)
Аналогично, дифференцируя первое из уравнений (4.34) по x, а второе –по t, и вычитая почленно одно из другого, имеем
(4.36)
Уравнения (4.35) и (4.36) описывают волну, распространяющуюся вдоль оси X со скоростью v. Это непосредственно видно из того, что любая функция f(t-x/v) является решением этого уравнения. Поэтому фронт волны f = const задается условием
t–x/v = const, (4.37)
из которого следует, что
(dx/dt) = v, (4.38)
т.е. v является действительно скоростью распространения фронта волны.
Решение уравнений (4.35) и (4.36) будем искать в следующем виде:
. (4.39)
Подставляя (4.39) в (4.34), получаем алгебраические уравнения для определения 
и 
:
(4.40)
откуда
, 
, (4.41)
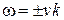. (4.42)
Соотношение (4.42) выражает связь существующую между частотой волны ω = 2π/ T и волновым числом k = 2π/λ, где T и λ – период колебаний и длина волны. Это соотношение называется дисперсионным. В данном случае оно имеет простой вид. Однако в других случаях оно может быть более сложным. Это соотношение позволяет определить частоты колебаний, а следовательно, и энергии соответствующих мод, если известны волновые числа.
Определение числа мод. В теле конечного размера возникают стоячие волны. Границы тела свободно колеблются, на них никакие напряжения не возникают. Возьмем тело в виде куба объемом L3 и поместим начало координат в одну из вершин. Рассмотрим плоские стоячие волны по оси X. Обозначим ξ - отклонение колеблющейся точки от положения равновесия. Поскольку поверхность куба свободна, на ней при колебаниях не возникают никакие напряжения, т.е. граничное условие имеет вид:
(4.43)
Решение уравнения (4.36), удовлетворяющее условиям (4.43), имеет вид:
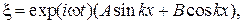(4.44)
где ω и k связаны равенством (4.42). Для того чтобы удовлетворить (4.43), надо в (4.44) положить A = 0, а на k наложить условие
kL = n π, (n= 1, 2 …).
Оно определяет дискретный набор волновых чисел, при которых возможно существование стоячих волн. Аналогичные формулы находятся и для других осей координат. Следовательно, получаем следующие наборы волновых чисел, каждому из которых соответствует стоячая волна, составляющая моду колебаний:
kx = π nx/L, ky = π ny/L, kz = π nz/L (4.45)
(nx=1,2,…), (ny=1,2,…), (nz=1,2,…),
Числа nx, ny, nz пробегают все возможные значения независимо. Подсчет числа мод сводится к определению числа различных троек числа (nx, ny, nz) или, другими словами, к подсчету числа точек, декартовы координаты которых равны (nx, ny, nz).
Число этих точек в объеме с длинами сторон 
, 
и 
равно . Следовательно, число мод, соответствующее этим числам,
, (4.46)
где 
= (L/π)dkx и т.д., как это непосредственно следует из (4.45). В правой части (4.46) написаны дифференциалы dkx, dky, dkz, потому что L много больше длины волн.
Для подсчета dN удобнее перейти к сферическим координатам (рис.4.3), принимая во внимание, что kx, ky, kz имеют лишь положительное значение. Это означает, что в (4.46) надо положить dkxdkrdkz = (4 π /8)k2dk. В результате для числа мод в интервале волновых чисел от k до k+dk (4.39) получаем выражение
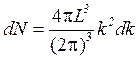, (4.47)
где множитель 4π сохранен без сокращения на (2π3) в знаменателе для того, чтобы подчеркнуть произведенный переход к сферическим координатам.
Далее воспользуемся соотношением (4.42), из которого следует, что
k2dk=(1/v3) ω2 d ω (4.48)
и, следовательно, число мод с частотой колебаний между ω и ω+ d ω равно
. (4.49)
Плотность мод. Число мод, отнесенное к интервалу частот, называется плотностью мод
ρ(ω) = dN/d ω. (4.50)
Поэтому из (4.9) следует, что
. (4.51)
Аналогичные расчеты можно провести для каждой из поперечных мод. В изотропном случае скорости обеих поперечных мод одинаковы. Обозначив скорости продольной и поперечной мод соответственно v при v пп и приняв во внимание, что плотность всех мод равна сумме плотностей отдельных мод, напишем
. (4.52)
Чтобы не усложнять обозначения в (4.52), полная плотность мод показана той же буквой, какой раньше в (4.51) была обозначена плотность мод одной из поляризаций.
Отметим, что по самому смыслу предшествующих расчетов формула (4.52) не может быть справедливой для очень коротких длин волн, поскольку мы пренебрегли атомной структурой твердого тела и проводили расчет так, как если бы оно состояло из непрерывно распределенной по его объему массы. Для волн, длина которых существенно превосходит среднее расстояние между атомами, а смещение атомов из положения равновесия не очень велики, формула (4.52) является справедливой. Именно этот случай и интересен при рассмотрении теплоемкости при низкой температуре.
С другой стороны, поскольку температура и kT очень малы, выражение (4.52) справедливо вплоть до частот, для которых ω >> kT. В этой области exp[ ω /(kT) ], входящая в знаменатель выражения (4.23), велика и, следовательно, среднее число мод с очень большими частотами экспоненциально мало. Это означает, что вклад от них в общую энергию очень мал. Поэтому, несмотря на то что выражение (4.52) для больших частот несправедливо, им можно пользоваться до сколь угодно больших частот, поскольку экспоненциальный множитель обратит в нуль вклад от этих частот в вычисляемые величины.
Теплоемкость при низкой температуре. Полная энергия всех мод колебаний, связанная с тепловой энергией, равна
(4.53)
Входящий в это выражение интеграл может быть вычислен методами функций комплексного переменного. Он равен 
Формула (4.53) позволяет вычислить теплоемкость
(4.54)
Такая зависимость теплоемкости от температуры вблизи температуры 0 К согласуется с данными эксперимента.
Температура Дебая. Строго говоря, все проведенные расчеты, в частности вывод дисперсионного соотношения, справедливы только для волн с достаточно большой длиной волны. Поэтому полученная на основе дисперсного соотношения формула (4.52) также справедлива лишь для таких же волн, т.к. для не слишком больших частот. Однако из замечаний о вкладе в теплоемкость волн с короткой длиной волны, сказанных в связи с формулой (4.52), следует, что мы не сделаем большой ошибки, если применим эту формулу также и для больших частот, вплоть до максимальной частоты ωмакс, определенной таким образом, чтобы полное число мод при этом было равно фактически имеющемуся числу мод 3 NA. Поэтому
(4.55)
Максимальная частота ωмакс зависит от упругих свойств материала. Вообще говоря, частота ωмакс может быть различной для различных направлений поляризации. Однако для упрощения формулы в (4.55) взята некоторая средняя максимальная частота. Подставив выражение (4.52) в (4.55) и проинтегрировав, получим
, (4.56)
где < v> - средняя скорость звука, определяемая соотношением
. (4.57)
Максимальную частоту, определенную в соответствии с условием (4.55), принято выражать через температуру Дебая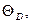 
получаемую из соотношения
k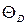 
= ωмакс. (4.58)
Обычно температура Дебая лежит в пределах от 100 до 1000 К. Например, для меди она равна примерно 340 К, а для алмаза – около 2000 К.
Теплоемкость при произвольной температуре. При вычислении энергии U в (4.53) не учитывалось наличие максимальной частоты ωмакс, определяемой формулой (4.55). Если это учесть, то интеграл необходимо ограничить частотой ωмакс. Тогда вместо формулы (4.53) получим
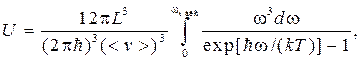(4.59)
где < v > определяется соотношением (4.57). Переходя при интегрировании к безразмерной переменной
ξ = ω/ (kT)
и принимая во внимание (4.56) и (4.58), получаем
(4.60)
Теплоемкость CV находим дифференцированием (4.54) по Т. При Т<< θDверхний предел интегрирования может быть распространен до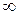 
, тогда получаем (4.54).
При Т >>θDверхний предел интегрирования близок к нулю и, следовательно, ξ в подынтегральном выражении очень малая величина, и можно считать, что exp 
Поэтому формула (4.60) принимает вид:
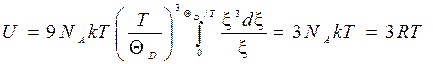. (4.61)
Следовательно, теплоемкость в этом случае равна
CV = (dU/dT) v = 3 R, (4.62)
т.е. так и должно быть в соответствии с законом Дюлонга и Пти.
При температуре T ~ 
интеграл в (4.52) не может быть вычислен аналитически и приходится пользоваться численными методами. Свойства различных материалов учитываются значением температуры Дебая 
. Поэтому кривая теплоемкости как функция отношения T/ является универсальной. Она показана на рис. 4.17 и находится в согласии с данными эксперимента.
Вывод формул для теплоемкости, исходя из представления о фононах. Для того чтобы освоиться с представлением о квазичастицах, полезно вывести формулу для теплоемкости твердого тела на основании представления о фононах.
Как уже было отмечено в связи с формулой (4.20), моду колебаний, несущую энергию ω, можно рассматривать как квазичастицу. При таком подходе тепловые колебания решетки сводятся к совокупности фононов, рассматриваемой как идеальный газ.
Энергия фонона в соответствии с (4.20) равна
ε = ω, (4.63)
а его импульс p связан с волновым числом k обычным соотношением для свободных частиц
p = k. (4.64)
Энергия и импульс фонона связаны соотношением (4.42), которое с учетом (4.63) и (4.64) может быть записано в виде
ε = < 
> p, (4.65)
где учтено наличие нескольких поляризаций фононов и взята их средняя скорость в соответствии с (4.57).
Плотность состояний газа, состоящего из фононов как квазичастиц, дается формулой в виде
dГ = ρ(ε) d ε = 3V4 π p2dp/(2 π h)3. (4.66)
Множитель 3 учитывает три возможных поляризации фононов. Принимая во внимание (4.64), из (4.57) получаем
(4.67)
Для дальнейших вычислений удобно выразить ρ(ε) не через среднюю скорость < v > звука, а через температуру Дебая, воспользовавшись условием, что общее число фононов должно быть равно
(4.68)
Тогда
ρ(ε) = 9N
