Контрольные задания
по курсу «Математические задачи электроэнергетики»
Для специальности ЭПП
Построение математической модели электрической цепи
Задача. Для заданной электрической схемы построить математическую модель электрической цепи методом узловых потенциалов и табличным методом.
Вариант контрольного задания определяется двумя последними цифрами номера зачетки. Если получаемое число больше 49, то следует для нахождения номера варианта вычесть 50.
Варианты задания
| № вар. | Рис. | R 1 | R 2 | R 3 | R 4 | R 5 | R 6 | E 1 | E 2 | E 3 | J 1 | J 2 | J 3 | |||||||||||||||
| Ом | В | А | ||||||||||||||||||||||||||
| 8.5 | — | — | 0,8 | |||||||||||||||||||||||||
| 8.6 | — | — | ||||||||||||||||||||||||||
| 8.14 | — | — | 0,4 | |||||||||||||||||||||||||
| 8.8 | — | — | 0,4 | |||||||||||||||||||||||||
| 8.9 | — | — | ||||||||||||||||||||||||||
| 8.15 | — | — | 0,5 | |||||||||||||||||||||||||
| 8.16 | — | 0,1 | — | |||||||||||||||||||||||||
| 8.7 | — | — | 0,1 | |||||||||||||||||||||||||
| 8.19 | — | — | ||||||||||||||||||||||||||
| 8.20 | — | 0,1 | — | |||||||||||||||||||||||||
| 8.3 | — | — | 0,5 | |||||||||||||||||||||||||
| 8.4 | — | 0,2 | — | |||||||||||||||||||||||||
| 8.12 | 10,5 | — | — | |||||||||||||||||||||||||
| 8.10 | — | — | ||||||||||||||||||||||||||
| 8.11 | — | — | 0,4 | |||||||||||||||||||||||||
| 8.1 | — | — | ||||||||||||||||||||||||||
| 8.2 | — | — | 0,5 | |||||||||||||||||||||||||
| 8.17 | — | — | 0,3 | |||||||||||||||||||||||||
| 8.18 | — | — | ||||||||||||||||||||||||||
| 8.13 | — | — | ||||||||||||||||||||||||||
| 8.5 | — | — | 0,4 | |||||||||||||||||||||||||
| 8.1 | — | — | ||||||||||||||||||||||||||
| 8.3 | — | — | 0,4 | |||||||||||||||||||||||||
| 8.16 | — | 0,1 | — | |||||||||||||||||||||||||
| 8.10 | — | — | ||||||||||||||||||||||||||
| 8.2 | — | — | ||||||||||||||||||||||||||
| 8.4 | — | 0,2 | — | |||||||||||||||||||||||||
| 8.7 | — | — | 0,2 | |||||||||||||||||||||||||
| 8.20 | — | 0,1 | — | |||||||||||||||||||||||||
| 8.19 | — | — | 0,5 | |||||||||||||||||||||||||
| 8.17 | — | — | 0,2 | |||||||||||||||||||||||||
| 8.8 | — | 0,4 | — | |||||||||||||||||||||||||
| 8.14 | — | — | 0,2 | |||||||||||||||||||||||||
| 8.12 | — | — | ||||||||||||||||||||||||||
| 8.9 | — | — | ||||||||||||||||||||||||||
| 8.10 | — | — | 0,5 | — | ||||||||||||||||||||||||
| 8.15 | — | — | 0,3 | |||||||||||||||||||||||||
Окончание табл.
| № вар. | Рис. | R 1 | R 2 | R 3 | R 4 | R 5 | R 6 | E 1 | E 2 | E 3 | J 1 | J 2 | J 3 | ||
| Ом | В | А | |||||||||||||
| 8.18 | — | 0,2 | — | ||||||||||||
| 8.6 | — | 0,5 | — | ||||||||||||
| 8.11 | — | — | |||||||||||||
| 8.5 | — | — | |||||||||||||
| 8.1 | — | — | 0,5 | ||||||||||||
| 8.3 | — | — | 1,5 | ||||||||||||
| 8.2 | — | — | |||||||||||||
| 8.14 | — | — | 0,5 | ||||||||||||
| 8.16 | — | 0,2 | — | ||||||||||||
| 8.13 | — | — | |||||||||||||
| 8.7 | — | — | 0,1 | ||||||||||||
| 8.20 | — | 0,1 | — | ||||||||||||
| 8.19 | — | — | |||||||||||||
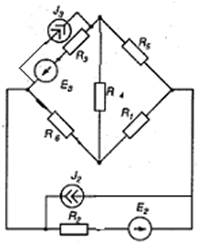

Рис. 8.1 Рис. 8.2
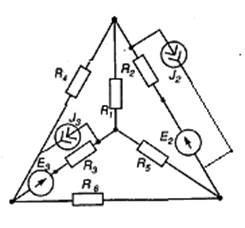

Рис. 8.3 Рис. 8.4


Рис. 8.5 Рис. 8.6

Рис. 8.7

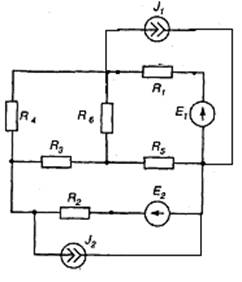
Рис. 8.8 Рис. 8.9


Рис. 8.10 Рис. 8.11

Рис. 8.12

Рис. 8.13

Рис. 8.14


Рис. 8.15 Рис. 8.16


Рис. 8.17 Рис. 8.18
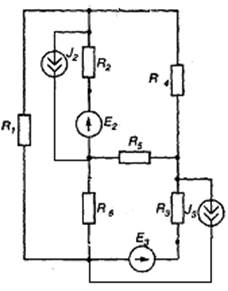

Рис. 8.19 Рис. 8.20
Литература
1. Норенков И.П. Введение в автоматизированное проектирование технических устройств и систем.- М.: Высш. шк., 1986.
2. Норенков И.П., Маничев В.Б. Системы автоматизированного проектирования электронной и вычислительной аппаратуры.- М.: Высш. шк., 1983.
3. Системы автоматизированного проектирования: в 9-ти кн. Кн.4 Математические модели технических объектов / В.А. Трудоношин, Н.В. Пивоваров.- М.: Высш. шк., 1986.
4. Моделирование статического и переходного режимов методом узловых потенциалов / Сивяков Б.К., Дмитриева Е.И. Метод. указания, СГТУ, Саратов, 1991.
5. Моделирование электронных схем табличным методом / Сивяков Б.К., Дмитриева Е.И. Метод. указания, СГТУ, Саратов, 1991.
Исследование статической устойчивости электрической системы
Задача. По заданному характеристическому многочлену:
D(p)= a0p5+ a1p4+ a2p3+ a3p2+ a4p+ a5
исследовать устойчивость электрической системы с помощью следующих методов:
1. Метода Гурвица. Следует определить также количество корней в правой полуплоскости.
2. Критерия Михайлова. Применить необходимые и достаточные условия, включающие перемежаемость корней уравнений.
3. Критерия Найквиста. Построить годограф разомкнутой системы W(jω).
4. Метода D-разбиения.
Примечания.
1. Коэффициенты многочлена a0, a1, a2, a3, a4 и a5 – цифры номера зачетки, цифра 0 заменяется цифрой 1.
2. При анализе устойчивости с помощью критерия Найквиста принять коэффициент передачи разомкнутой петли обратной связи системы W(p) = D(p).
3. В методе D-разбиения построить область статической устойчивости в координатах коэффициентов усиления K2, K1 электрической системы, заданной характеристическим уравнением: D(p)= a0p5+ a1p4+ a2p3+ a3p2(1+ K2)+ a4p(1+ K1)+ a5= 0.
Литература
1. Электрические системы. Математические задачи электроэнергетики / Веников В.А., Зуев Э.Н. и др. М.: Высш. шк., 1981.
Оптимизация распределения нагрузки между
тремя агрегатами ГЭС методом динамического программирования
Задача. Необходимо распределить суммарную часовую нагрузку гидроэлектростанции ГЭС P’∑ (МВт) между тремя её агрегатами так, чтобы получить минимум расхода воды QГЭС (м3/с). Расходные характеристики агрегатов известны (табл.1). Задачу решить методом динамического программирования. Построить график оптимальной нагрузки агрегатов при изменении суммарной нагрузки от 0 до 300 МВт с шагом в 50 МВт.
Таблица 1. Расходные характеристики агрегатов
| Нагрузка агрегата, Мвт | P`1 = 0 | P`2 = 50 | P`3 = 60 | P`4 = 70 | P`5 = 80 | P`6 =90 | P`7 = 100 |
| Агрегат № 1 | Q11 | Q12 | Q13 | Q14 | Q15 | Q16 | Q17 |
| Агрегат № 2 | Q21 | Q22 | Q23 | Q24 | Q25 | Q26 | Q27 |
| Агрегат № 3 | Q31 | Q32 | Q33 | Q34 | Q35 | Q36 | Q37 |
Табл.1 заполняется согласно варианту задания данными из табл. 2.
Таблица 2. Варианты задания
| № вар. | Расход воды Qi (м3/с) в зависимости от нагрузки P`I агрегатов (МВт) | Шаг h, МВт | ||||||
Примечания.
1. Вариант выбирается по трем последним цифрам зачетки, например, 724 – агрегату №1 соответствует 7 строка, агрегату №2 соответствует 2 строка и агрегату №3 соответствует 4 строка табл. 2.
2. Если цифра в номере зачетки встречается дважды (трижды), то повторяющиеся цифры берутся из второй (третьей) десятки (от 0 до 9) строк табл. 2.
3. График оптимальной нагрузки агрегатов при изменении суммарной нагрузки от 0 до 300 МВт с шагом в 50 МВт представляет собой зависимости P1опт, P2опт и P3опт от P’∑, построенные в одних координатах.
Литература
1. Арион В.Д., Журавлев В.Г. Применение динамического программирования к задачам электроэнергетики.- Кишинев: Штиница, 1981.
2. Применение алгоритма динамического программирования при выборе оптимального состава и распределении нагрузки между агрегатами / Кубарева Т.С. Метод. указания, СГТУ, Саратов, 1993.






