Седиментационный анализ суспензии кварца в воде

 

Цель: исследование кинетики седиментации суспензии кварца в воде, определение фракционного состава.

 

Оборудование и реактивы: торсионные весы с чашечкой для взвешивания, стеклянный цилиндр емкостью 1 литр, мерный цилиндр емкостью 250 – 500 мл, мешалка (диск с отверстиями, закрепленный на стержне), секундомер, фарфоровая ступка с пестиком, аналитические весы, сито с размером отверстий 0,1 мм, анализируемый дисперсный материал (молотый кварц, сульфат бария или оксид алюминия, дистиллированная вода.

Теоретические пояснения

 

Важнейшими характеристиками многих дисперсных систем с жидкой дисперсионной средой являются размер и форма частиц, так как многие свойства таких систем определяются именно этими параметрами. Кроме того, реальные дисперсные системы, как правило, полидисперсны, и для описания их свойств недостаточно знать некий средний размер частиц. Необходимо установить распределение частиц по размерам. Это является задачей дисперсионного анализа. Седиментационный анализ представляет собой один из методов дисперсионного анализа.

В основе седиментационного анализа лежит зависимость линейной скорости осаждения частиц дисперсной фазы в гравитационном поле от их размеров.

Если сферическую частицу, радиус которой r и плотность ρ, поместить в жидкость, плотность которой равна ρ_ж, а вязкость η, на нее будет действовать сила седиментации F_cед, представляющая собой равнодействующую силы тяжести и выталкивающей силы. На движущуюся частицу также действует сила сопротивления среды.

Вначале частица движется ускоренно, так как при малых скоростях сила тяжести превышает силу сопротивления среды. По мере увеличения скорости движения v сила сопротивления среды возрастает в соответствии с уравнением Стокса

(6.1)

и в некоторый момент достигается равенство силы седиментации и силы сопротивления среды. Начиная с этого момента, частица движется с постоянной скоростью. Время, которое требуется для достижения равномерного движения частицы, пренебрежимо мало. Так для частицы кварца радиусом 5·10^-5м это время составляет 3,4 ·10^-3с.

При равномерном движении частицы

. (6.2)

Для частицы сферической формы

.

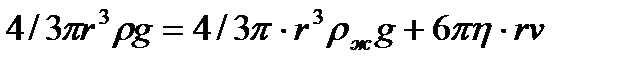. (6.3)

Итак, скорость частицы прямо пропорциональна квадрату ее радиуса. Если экспериментально определить скорость оседания, то можно определить радиус частицы.

 

или (6.4)

 

Скорость седиментации можно рассчитать как

, (6.5)

то есть как отношение высоты столба суспензии ко времени седиментации.

. (6.6)

Это уравнение справедливо только при условиях выполнения закона Стокса:

˗ частицы имеют сферическую форму;

˗ частицы движутся с постоянной скоростью и независимо друг от друга;

˗ движение жидкости вблизи частицы является ламинарным;

˗ для дисперсионной среды трение является внутренним, то есть определяется трением при смещении слоев жидкости друг относительно друга.

Эти условия выполняются для частиц размером 10^-6 – 10^-4м при концентрациях дисперсной фазы 0,5 – 0,6% и полном смачивании частиц жидкостью.

Поскольку большинство реальных дисперсных систем имеют частицы неправильной формы, то при седиментационном анализе определяется радиус эквивалентной сферы, то есть радиус частиц сферической формы, оседающих с той же скоростью, что и реальные частицы неправильной формы.

Первым этапом седиментационного анализа является экспериментальное получение кривой седиментации, то есть зависимости массы осевших частиц дисперсной фазы от времени осаждения.

Массу осадка m_i к моменту времени τ_i определяют при помощи торсионных весов (рисунок 6.1).

Для получения кривой седиментации с помощью торсионных весов определяют изменение массы чашки 8, за счет оседания частиц дисперсной фазы. Чашку помещают в стеклянный цилиндр 7 с суспензией исследуемого порошка.

Диаметр цилиндра должен быть подобран таким образом, чтобы расстояние между его стенками и краями чашечки составляло не менее 3 мм. При меньших зазорах на осаждении частиц будут сказываться пристеночные эффекты. Расстояние от чашечки до дна цилиндра должно составлять не более 2—3 см (при больших расстояниях могут быть не учтены самые крупные частицы), от дна чашечки до поверхности суспензии около 15—20 см (высота h).

 

 

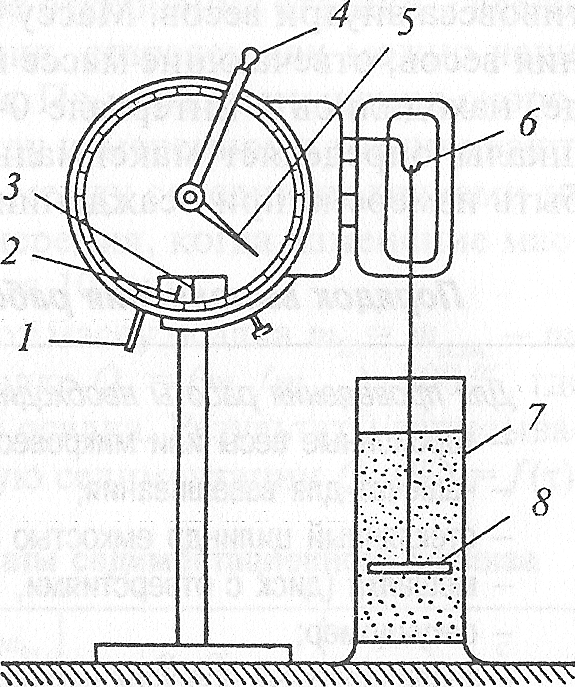
Рисунок 6.1 – Схема торсионных весов: 1 – арретир; 2 – стрелка весов; 3 – риска; 4 – рычаг уравновешивания; 5 – стрелка циферблата; 6 – крючок для чашки; 7 – стеклянный цилиндр; 8 – чашка весов

 

Чашечка подвешивается на крючок 6, которым заканчивается коромысло весов. При этом необходимо проследить, чтобы ось чашечки совпадала с осью цилиндра.

Для проведения измерений арретир весов 1 перемещают в крайнее правое положение (при этом стрелка циферблата 5 должна находиться против нуля шкалы). Стрелка весов 2 при этом отклоняется влево от риски 3. Осторожным поворотом рычага 4 против часовой стрелки совмещают стрелку 2 с риской 3. Отсчитывают показания (в мг) по положению стрелки 5.

Торсионные весы, как правило, рассчитаны на измерение навесок в пределах 0—500 мг. Учитывая, что масса чашечки в дисперсионной среде может быть больше верхнего предела шкалы, торсионные весы тарируют с помощью груза, установленного на рычаге противовеса внутри весов. Массу груза подбирают такой, чтобы показания весов, отвечающие массе пустой чашки в дисперсионной среде, находились в интервале 0 – 100 мг. Оставшаяся до 500 мг часть шкалы определяет максимальную массу порошка, которая может быть измерена при осаждении его на чашке.

Для монодисперсных систем зависимость m=f(τ) должна иметь вид прямых, проходящих через начало координат.

. (6.7)

Если в дисперсной системе содержатся частицы разных размеров эта зависимость графически выражается кривой выпуклой формы, которая стремится к пределу, равному массе всех частиц, имеющихся в дисперсной системе.

Масса частиц , осевших к моменту времени , выражается уравнением Одена:

, (6.8)

где m_i – масса частиц тех фракций, которые полностью выпали в осадок к моменту времени τ_i.

Второе слагаемое определяет массу частиц во фракциях, выпавших лишь частично.

Так как абсолютные массы осадка будут зависеть от исходной массы дисперсной фазы, то рассчитывают относительные массы осадка Q в %.

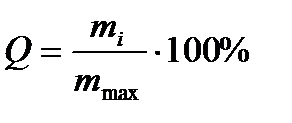. (6.9)

Величина m_max равна массе всех частиц, которые находятся в столбе суспензии над чашкой торсионных весов и может быть рассчитана по формуле

, (6.10)

где S – площадь чашки весов;

h – высота столба суспензии;

С – концентрация вещества дисперсной фазы, мг/м³.

Если все величины измеряются в единицах системы СИ, то масса будет измеряться в мг.

Уравнение Одена приобретает следующий вид:

(6.11)

Рисунок 6.2 – Кривая седиментации

 

Если в точке, соответствующей моменту времени τ_i, провести касательную к кривой седиментации, то отрезок, отсекаемый на оси ординат, будет равен Q_i, то есть относительной массе частиц тех фракций, которые полностью выпали в осадок к моменту времени τ_i.

На основании седиментационной кривой можно рассчитать по уравнению (1) радиусы самых крупных частиц. Для этого в уравнение (1) нужно подставить время, соответствующее концу линейного участка графика. Радиусы самых маленьких частиц можно вычислить при подстановке в уравнение (1) времени, соответствующему началу горизонтального отрезка графика.

Для установления фракционного состава дисперсной фазы на основе кривой седиментации (рисунок 6.3) необходимо построить интегральную кривую распределения , как показано на рисунке 6.4. Каждая ордината Q_i на интегральной кривой распределения указывает процентное содержание частиц, обладающих радиусом, равным или большим соответствующей абсциссе r_i.

На основании интегральной кривой распределения можно определить процентное содержание определенных фракций. Так процентное содержание фракции с радиусами частиц от r₂ до r₁ равно ΔQ=Q₂-Q₁.

Дифференциальную кривую распределения можно построить, как показано на рисунке 6.5, на основании интегральной кривой, находя графически значения ΔQ_i для серий фракций Δr_i. Полученное значение относят к среднему для данной фракции радиусу.

Максимум на дифференциальной кривой распределения соответствует радиусу частиц, наиболее распространенных в данной дисперсионной системе.

Процентное содержание определенной фракции соответствует площади под соответствующим участком кривой.

 

Методика проведения опыта

 

Дисперсный материал истолочь в фарфоровой ступке и просеять через сито с размером отверстий 0,1 мм.

Взвесить на аналитических весах 3 – 5 г просеянного материала (в соответствии с указаниями преподавателя).

Измерить диаметр чашечки для последующего определения площади ее поверхности.

Определить показание торсионных весов, соответствующее массе пустой чашечки m₀ в дистиллированной воде. Для этого в цилиндр налить 1 литр воды и сделать отметку по нижнему краю мениска. Чашечку опустить в воду, несколько раз резко повернув вокруг оси, чтобы избавиться от прилипших пузырьков воздуха. Чтобы зафиксировать положение цилиндра, при котором чашечка располагается вдоль его оси, можно под него подложить бумагу и обвести на ней дно сосуда.

Измерить линейкой глубину погружения чашечки h.

Вынуть на время чашечку из воды.

В лабораторном журнале записать значения массы порошка m, массы пустой чашечки в воде m₀, диаметра чашечки d, глубины погружения чашечки h.

Приготовить суспензию, для чего навеску порошка высыпать в цилиндр с дистиллированной водой и плавными движениями мешалки вверх – вниз добиться равномерного распределения порошка по всему объему.

Цилиндр быстро устанавливают в нужное положение и быстро погружают в его содержимое измерительную чашечку. Тут же включают секундомер и весы и начинают добиваться равновесия весов, совмещая стрелку 2 с риской 3. Совместив, записывают первый отсчет массы чашечки m_i и времени τ_i.

Далее, по мере отклонения стрелки 2 влево, возвращают ее в положение равновесия, стараясь как можно чаще производить отсчеты массы и времени. По мере уменьшения скорости оседания интервалы времени между измерениями увеличивают. Желательно, чтобы изменения массы между соседними измерениями не превышали 5 мг.

Опыт считается законченным, когда изменения массы будут составлять менее 1мг за 10 минут.

Результаты опыта занести в таблицу 6.1.

Проделать необходимые расчеты, заполнить таблицы 6.1, 6.2, 6.3, построить седиментационную кривую, интегральную и дифференциальную кривые распределения.