Задача
По территориям региона приводятся данные за 201Х год (табл.2). Требуется:
1. Построить поле корреляции.
2. Для характеристики зависимости у от х:
а) построить линейное уравнение парной регрессии у от х;
б) оценить тесноту связи с помощью показателей корреляции и коэффициента детерминации;
в) оценить качество линейного уравнения с помощью средней ошибки аппроксимации;
г) дать оценку силы связи с помощью среднего коэффициента эластичности и бета – коэффициента;
д) оценить статистическую надежность результатов регрессионного моделирования с помощью F – критерия Фишера;
е) оценить статистическую значимость параметров регрессии и корреляции.
3. Проверить результаты, полученные в п. 2 с помощью ППП Excel.
4. Рассчитать параметры показательной парной регрессии. Проверить результаты с помощью ППП Excel. Оценить статистическую надежность указанной модели с помощью F – критерия Фишера.
5. Обоснованно выбрать лучшую модель и рассчитать по ней прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от среднего уровня. Определить доверительный интервал прогноза при уровне значимости g = 0,05.
Таблица 2
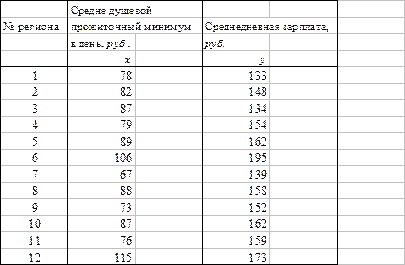
Решение
1. Построим поле корреляции, для чего отложим на плоскости в прямоугольной системе координат точки (хi, уi) (рис 1.)
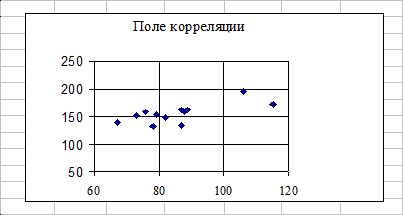
Рисунок 1
2. Для расчета параметров линейной регрессии строим расчетную таблицу 3
Таблица 3
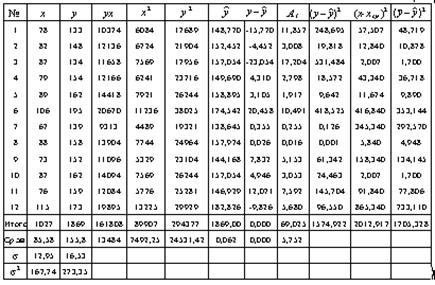
2 а) Построим линейное уравнение парной регрессии у по х. Используя данные таблицы 3, имеем
,
.
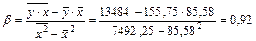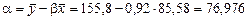Тогда линейное уравнение парной регрессии имеет вид
.
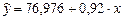Оно показывает, что с увеличением среднедушевого прожиточного минимума на 1 руб. средняя зарплата возрастает в среднем на 0,92 руб.
2 б) Учитывая:
, 
,
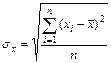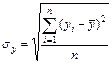оценим тесноту линейной связи с помощью линейного коэффициента парной корреляции:
.
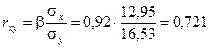Найдем коэффициент детерминации
.
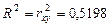Это означает, что почти 52% вариации заработной платы у объясняется вариацией фактора х – среднедушевого прожиточного минимума.
2 в) Для оценки качества полученной модели найдем среднюю ошибку аппроксимации
.
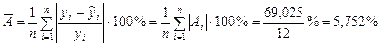В среднем, расчетные значения отклоняются от фактических на 5,752%. Качество построенной модели оценивается как хорошее, т.к. значение 
– менее 8 %.
2 г) Для оценки силы связи признаков у и х найдем средний коэффициент эластичности:
.
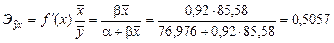Таким образом, в среднем на 0,5% по совокупности изменится среднедневная зарплата от своей средней величины при изменении среднедушевого прожиточного минимума в день одного трудоспособного на 1%.
Бета–коэффициент
,
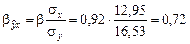показывает, что среднее квадратическое отклонение среднедневной зарплаты изменится в среднем на 72% от своего значения при изменении прожиточного минимума в день одного трудоспособного на величину его среднего квадратического отклонения.
2 д) Для оценки статистической надежности результатов используем F – критерий Фишера.
Выдвигаем нулевую гипотезу Н о о статистической незначимости полученного линейного уравнения.
Рассчитаем фактическое значение F – критерия при заданном уровне значимости g = 0,05:
.
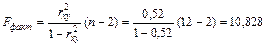Сравнивая табличное Fтабл =4,96 и фактическое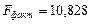 
значения, отмечаем, что
,
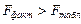что указывает на необходимость отвергнуть выдвинутую гипотезу Н о.
2 е) Оценку статистической значимости параметров регрессии проведем с помощью t – статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей.
Выдвигаем гипотезу H 0 о статистически незначимом отличии показателей регрессии от нуля: a = b = rxy = 0.
Табличное значение t – статистики tтабл для числа степеней свободы
df = n – 2 = 12 – 2 = 10
при заданном уровне значимости g = 0,05 составляет 2,23.
Определим величину случайных ошибок
,
,
.
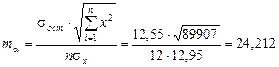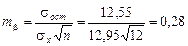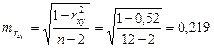Найдем соответствующие фактические значения t – критерия Стьюдента
, 
,
.
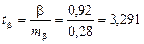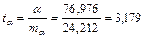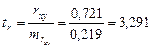Фактические значения t – статистики превосходят табличное значение tтабл= 2,23
, 
, 
,
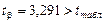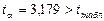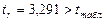поэтому гипотеза H 0 о статистически незначимом отличии показателей регрессии от нуля отклоняется, т.е. параметры a,b и rxy не случайно отличаются от нуля, а статистически значимы.
Для расчета доверительных интервалов для параметров a и b определим их предельные ошибки
,
.
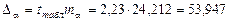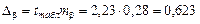Доверительные интервалы
для параметра a: (23,029; 130,923),
для параметра b: (0,297; 1,5436).
С вероятностью
р = 1 – g = 1 – 0,05 = 0,95
можно утверждать, что параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
3. Проверим результаты, полученные в п. 2 с помощью ППП Excel.
Параметры парной регрессии вида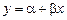 
определяет встроенная статистическая функция ЛИНЕЙН. Порядок вычисления следующий:
1) ведите исходные данные или откройте существующий файл, содержащий анализируемые данные;
2) выделите область пустых ячеек 5х2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики;
3) активизируйте Мастер функций любым из способов:
а) в главном меню выберете Вставка/Функция;
б) на панели Стандартная щелкните по кнопке Вставка функции (рис. 4)
(в результате появится диалоговое окно Мастер функций (рис. 2));
4) в окне Категория(рис. 2) выберите Статистические, в окне Функция – ЛИНЕЙН. Щелкните по кнопке ОК (в результате появится диалоговое окно ввода аргументов функции ЛИНЕЙН (рис. 3));
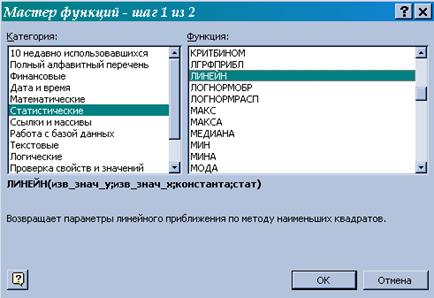
Рисунок 2. Диалоговое окно «Мастер функций»
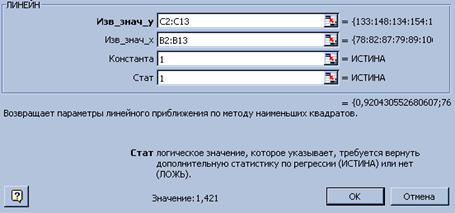
Рисунок 3. Диалоговое окно ввода аргументов функции ЛИНЕЙН
5) заполните аргументы функции (рис. 3):
Известные значения у – диапазон, содержащий данные ре- зультативного признака;
Известные значения х – диапазон, содержащий данные факторов независимого признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается свободным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения
Щелкните кнопкой ОК;
6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу. Нажмите клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме (табл. 4)
Таблица 4
| Значение коэффициента b | Значение коэффициента a |
| Среднее квадратическое отклонение b | Среднее квадратическое отклонение a |
| Коэффициент детерминации R 2 | Cреднеквадратическое отклонение у |
| F – статистика | Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
Для данных рассматриваемого примера результат вычисления функции ЛИНЕЙН представлен на рис. 4
Мастер функции
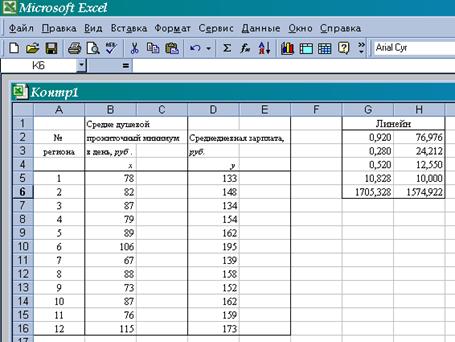
Рисунок 4. Результат вычисления функции ЛИНЕЙН
Замечание
С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:
1) проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис / Настройки. Установите флажок Пакет анализа (рис. 5);
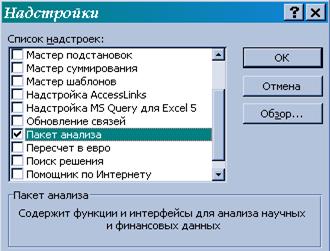
Рисунок 5. Подключение надстройки Пакет анализа
2) в главном меню выберите Сервис / Анализ данных / Регрессия (рис. 6). Щелкните по кнопке ОК;
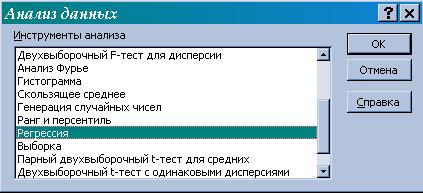
Рисунок 6. Диалоговое окно Анализ данных
3) заполните диалоговое окно ввода данных и параметров вывода (рис. 7):
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал Х – диапазон, содержащий данные факторов независимого признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – нуль – флажок, указывающий на наличие или на отсутствие свободного члена в уравнении;
Входной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа.
Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните кнопкой ОК.
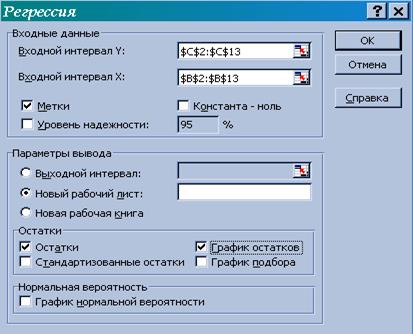
Рисунок 7. Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных рассматриваемой задачи представлены на рис. 8
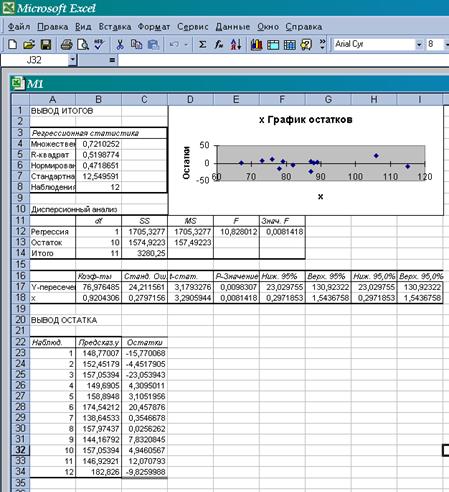
Рисунок 8. Результаты применения инструмента Регрессия
Сравнивая полученные вручную и с помощью ППП Excel данные, убеждаемся в правильности выполненных действий.
4. Построению показательной модели
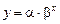(2)
предшествует процедура линеаризации переменных.
Прологарифмируем обе части уравнения (2), получим
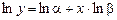. (3)
Введем обозначения
, 
, 
.
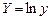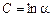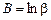Тогда уравнение (3) запишется в виде
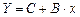. (4)
Параметры полученной линейной модели (4) рассчитываем аналогично тому, как это было сделано выше. Используем данные расчетной таблицы 5
Таблица 5
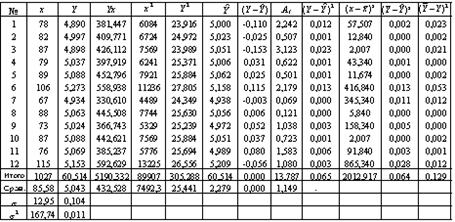
Построим линейное уравнение парной регрессии Y по х. Используя данные таблицы 5, имеем
,
.
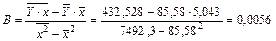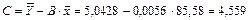Получим линейное уравнение регрессии:
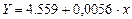. (5)
Тесноту полученной линейной модели характеризует линейный коэффициент парной корреляции
.
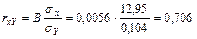Коэффициент детерминации при этом равен
.
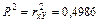Это означает, что почти 50% вариации фактора Y объясняется вариацией фактора х.
Средняя ошибка линейной аппроксимации составляет
.
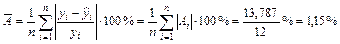Проведя потенцирование уравнения (5), получим искомую нелинейную (показательную) модель
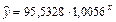. (6)
Результаты вычисления параметров показательной кривой (2) можно проверить с помощью ППП Excel, для чего используем встроенную статистическую функцию ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН.
В результате применения функции ЛГРФПРИБЛ дополнительная регрессионная статистика будет выводиться в порядке, указанном выше (табл. 4), причем в первой строке таблицы (рис. 9) функция ЛГРФПРИБЛ возвращает коэффициенты показательной модели (2), остальные параметры соответствуют линейной модели (4) (рис. 9).
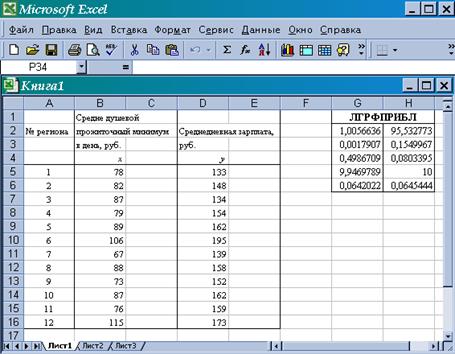
Рисунок 9. Результат вычисления функции ЛГРФПРИБЛ
Для расчета индекса корреляции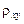 
нелинейной регрессии воспользуемся вспомогательной таблицей 6.
Таблица 6
.
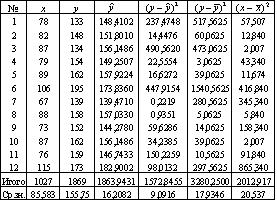
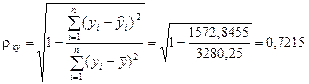Найдем коэффициент детерминации
.
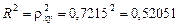Это означает, что 52% вариации заработной платы у объясняется вариацией фактора х – среднедушевого прожиточного минимума.
Рассчитаем фактическое значение F – критерия при заданном уровне значимости g = 0,05
.
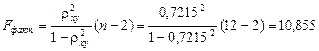Сравнивая табличное Fтабл =4,96 и фактическое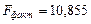 
значения, отмечаем, что
,
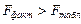что указывает на необходимость отвергнуть гипотезу Н о о статистически незначимых параметрах уравнения (6).
5. Так как коэффициенты детерминации, соответствующие линейной и показательной моделям практически равны (около 52% вариации заработной платы у объясняется вариацией фактора х – среднедушевого прожиточного минимума в обеих моделях), то нет весомых оснований отдать предпочтение какой либо модели. Тем не менее, прогнозное значение результата рассчитаем по показательной модели (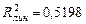
< 
).
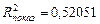По условию задачи прогнозное значение фактора выше его среднего уровня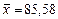 
на 5%, тогда оно составляет
,
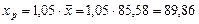и прогнозное значение зарплаты при этом составит
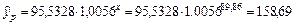руб.
Найдем ошибку прогноза
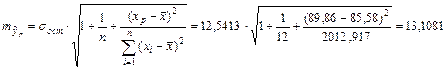
и доверительный интервал прогноза при уровне значимости g = 0,05.
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит
.
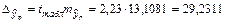Доверительный интервал прогноза
(129,4589; 187,9211).
Варианты заданий по первой части курсовой работы
В таблице 7 приведены данные по территориям региона за 201Х год. Число k рассчитывается по формуле
k = 100 + 10× i + j,
где i, j – две последние цифры зачетной книжки соответственно.
Требуется:
1. Построить поле корреляции.
2. Для характеристики зависимости у от х:
а) построить линейное уравнение парной регрессии у от х;
б) оценить тесноту связи с помощью показателей корреляции и коэффициента детерминации;
в) оценить качество линейного уравнения с помощью средней ошибки аппроксимации;
г) дать оценку силы связи с помощью среднего коэффициента эластичности и бета – коэффициента;
д) оценить статистическую надежность результатов регрессионного моделирования с помощью F – критерия Фишера.
е) оценить статистическую значимость параметров регрессии и корреляции.
3. Проверить результаты, полученные в п. 2 с помощью ППП Excel.
4. Рассчитать параметры показательной парной регрессии. Проверить результаты с помощью ППП Excel. Оценить статистическую надежность указанной модели с помощью F – критерия Фишера.
5. Обоснованно выбрать лучшую модель и рассчитать по ней прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от среднего уровня. Определить доверительный интервал прогноза при уровне значимости g = 0,05.
Таблица 7
| № региона | Среднедушевой прожиточный минимум в день, руб. х | Среднедневная зарплата, руб. у |
| k +2× i | ||
| k – 4× j | ||
| k + j | ||
| k – 3× i | ||
| k + i | ||
| k – 5× i | ||
| k – j | ||
| k + 2× j | ||
| k – i | ||
| k + 4× i | ||
| k – 3× j | ||
| k |
Литература
1. Доугерти К. Введение в эконометрику.– М.: Финансы и статистика, 1999.
2. Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика: Начальный курс.– М.: Дело, 2001.
3. Эконометрика. Под ред. И. И. Елисеевой.– М.: Финансы и статистика, 2001.
4. Афанасьев В. Н., Юзбашев М. М. Анализ временных рядов и прогнозирование.– М.: Финансы и статистика, 2001.
5. Экономико–математические методы и прикладные модели. Под ред. В. В. Федосеева.– М.: ЮНИТИ, 2001.
5. Экономико–математические методы и модели. Под ред. А. В. Кузнецова.– Минск: БГЭУ, 2000.
4. Кулинич Е. И. Эконометрика.– М.: Финансы и статистика, 2001.
Приложения
1. Критические значения t – критерия Стьюдента
