Задачи на экзамен и рейтинг-контроль.
I раздел: Алгебра.
1.Решить систему уравнений (методомГаусса, Крамера, матричным
методом). Пояснить процесс решения и сделать проверку:
2. Вычислить определитель матрицы (два способа – разложением по строке - столбцу
или правилом Саррюса):
3. Решить матричное уравнение (т.е. найти все подходящие матрицы Х) и сделать
проверку: A * X = B; X * A = B; A * X * B = C, где
A =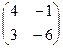 
; B = 
; C = 
;
4. Найти собственные значения и собственные векторы оператора, заданного матрицей:
; 
II раздел. Векторы.
1. Даны векторы a и b: │a │= 2, │b │ = 3, (a, ^ b) = 60°.
Используя ее, средствами векторного исчисления найти: площадь треугольника,
построенного на векторах c = (a + 3b) и d = (2a - b), а также величину угла между
c и d. Сделать соответствующий чертеж.
2. Дано: │c│ = │3a - 2b│ = 5, │d │= │-5a + 6b│ = 4, (c, ^ d) = 2π /6. Найти вели-
чину проекции вектора a на вектор b. Сделать схематический рисунок.
3. При каком значении параметра t векторы a = i + j + t k, b = i+ j + (t+1) k,
c = i – j – 2 t k а) будут компланарны? б) образуют тетраэдр объемом 5 куб. ед.?
4. Даны три вершины трапеции: A (3, 0), B (-1, 2), C (2, 5). Найти координаты ее
четвертой вершины D и длину средней линии, если известно, что | AB | = 3 | CD |
и AB || CD. Сделать подтверждающий чертеж.
5. Дана информация о векторах: │a │= 11, │b │ = 2 3, | a + b | = 30. Рассчитать
величину | a – b |. Сделать соответствующий чертеж.
6. Найти координаты вектора p, коллинеарного вектору q = { 2, 2, -1 } имеющего
длину 3 и образующего тупой угол с базисным вектором k.
7. Найти координаты единичного вектора a, перпендикулярного векторам b = { 1,1,1 }
и c = { 1, 3, -1 } и образующего острый угол с базисным вектором j.
8. Найти координаты вектора b, компланарного с векторами i, j, перпендикулярного
вектору a = { 4, - 3, 5 } и имеющего длину, равную 2 | a |.
III раздел. Геометрия.
1. Даны вершины треугольника: А (7; 2), B (1; 9), C (- 8; - 11). Рассчитать:
а) площадь, углы и периметр ∆ - ка АВС;
б) координаты центра и радиус описанной окружности; радиус вписанной окруж-ти;
в) координаты точки K – пересечения медианы АЕ с высотой BD;
г) длину высоты CF и координаты ее основания – точки F;
3. Даны координаты точек: A(0, 4, 3), B (4, 8, 1), C (2, 15, - 7), D (0, 6, 4).
Доказать, что тетраэдр с вершинами в этих точках существует и рассчитать:
а) площадь ABC;
б) объем пирамиды;
в) длину высоты пирамиды AE;
г) величину угла (≈ в градусах) между ребром CD и гранью ACD;
4. а) дана прямая: -4 x + 5 y + 20 = 0. Представить ее уравнение в других формах
и построить рисунок. То же – для прямой 2 x + 5 = 0.
Найти угол между этими прямыми.
б) даны уравнения плоскостей: x + 3 y – 2 z + 1 = 0 и - 2 x + y + 3 z + 6 = 0.
Написать уравнение линии их пересечения и найти расстояние от нее до плоскости
– 4 x + 2 y + 6 z – 3 = 0.
5. Привести уравнение кривой второго порядка к каноническому виду; установить, тип
кривой; указать её характеристики; построить чертёж:
; 
; 
.
IV раздел. Введение в математический анализ.
1. Указать тип неопределенности и вычислить предел (без помощи производной!)
lim (x3-2x-1) / (5x4 + 4x+1);
x→ -∞
lim (16 + 5 x) 2/ (x + 3) ; lim (cos (7x) – cos (3x)) / (π – x) 2 ;
x→ - 3 x→ π
2. Определить порядок бесконечно малой величины 
по сравнению с
бесконечно малой x при 
.
3. Доказать, что функция Y= f(x) непрерывна в точке x0:
Y=5x2-1,x0=6; Y=5x2+3,x0=8 .
4. Найти точки разрыва функции и установить их характер:
; 
; 
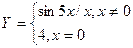
V раздел. Производные и исследование функций.
1. Рассчитать производную функции и указать её область определения:
__________
1. а) y = (5x – 6) / (√ x 3 + 5x - 6); б) y = [ (3 ) ctg (1 – 2x) + ln [ sin (x/2) ] 4 ;
___________________
в) y = log3 [ (√ (4x2 + 1) / (1 – 8x3) ]; г) y = [ arctg (2x+1) ] ln (cos x).
2. Найти дифференциал функций:
3. Найти производные 1-го и 2-го порядка функции, заданной параметрически
4. Найти производную y´ (x) неявной функции
5. Составить уравнение касательной и нормали к кривой:
в точке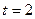 
.
6. Найти предел, используя правило Лопиталя
.
7. Исследовать функцию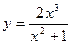 
и построить ее график.
8. Вычислить значение производных 1-го и 2 - го порядка в заданной точке to = 1
для функции y (x), заданной параметрически:
_____
x (t) = arctg 2t, y (t) = ln [(√ t 2 + 2)/ (2 t+ 1)].
9. Найти производную 1 - го порядка (с помощью логарифмирования):
f (x) = (sin x) arccos (ln2x)
10. Вычислить значение производной 1 – го порядка в заданной точке xo = – 1
для функции y (x), заданной неявно с помощью уравнения:
ln (2 y 2 + x ) = 4 x 2 y 3 –18.
11. Рассчитать приближенное значение величин (с помощью дифференциала
функции): ____
√ 22; lg 13.
12. Для функции y = (3x – 4) · (e) – x - 2 найти экстремумы и точки перегиба.
VI раздел. Функции нескольких переменных.
1. Найти: a) 
, где 
2. Найти dz (дифференциал первого порядка функции 
)
3. Вычислить приближенно: 
4. Найти экстремумы функции: 
5. Написать уравнение касательной плоскости в точке М(1.1.3): 