Вопросы к экзамену
2. Правило суммы. Правило произведения. Соединения без повторений (размещения, сочетания, перестановки).
3.Соединения с повторениями.
4. Биномиальные коэффициенты, их комбинаторный смысл. Основные тождества с биномиальными коэффициентами. Треугольник Паскаля. Бином Ньютона.
5. Полиномиальная теорема.
6. Метод включения-исключения.
7. Основные понятия графа. Лемма о рукопожатиях.
8. Способы задания графа.
9. Части графа. Операции над графами.
10. Маршруты, цепи, циклы в графах.
11. Связные компоненты графа.
12. Расстояния в графе.
13. Изоморфизм графов.
14. Эйлеровы цепи и циклы. Критерий эйлеровости графа.
15. Гамильтоновы цепи и циклы. Достаточные условия гамильтоновости графа. Метод Робертса и Флореса. Метод ветвей и границ. Задача коммивояжера.
16. Деревья. Лес. Характеристические свойства деревьев.
17. Ориентированные деревья.
18. Теорема Кэли о числе деревьев с занумерованными вершинами. Алгоритм Пруфера.
19. Остов графа. Цикломатическое число графа. Обходы графов по ширине и глубине.
20. Минимальные остовные деревья нагруженных графов. Алгоритмы Прима и Красколы.
21. Кратчайший путь в графе. Алгоритм Дейкстры.
22. Планарные графы. Теорема Эйлера и следствия из нее.
23. Двудольные графы. Признак двудольности. Паросочетания в двудольном графе.
24. Раскраска вершин графа. Теорема о пяти красках.
25. Алгоритмы раскраски графов.
26 Множества и операции над ними. Свойства операций. Доказать (АÈВ)/=А/ ÇВ/.
Доказать (АÇВ)ÈС = (АÈС)Ç(ВÈС) и (АÇВ)/ = А/ ÈВ/.
27. Декартово произведение множеств. Число элементов декартового произведения двух конечных множеств.
28.Дистрибутивность декартового умножения относительно объединения и разности.
29. Бинарные отношения и их основные свойства. Примеры. Инверсия отношения. Область определения и множество значений отношения.
30. Основные виды отношений (эквивалентность, упорядоченность, функции или отображения).
31. Функции или отображения. Классификация функций.
- Элементарные булевы функции. Число булевых функций. Существенные и несущественные переменные.
- Нормальные формы. Построение СДНФ и СКНФ.
- Полнота классов булевых функций. Критерий полноты Поста – Яблонского.
- Задача минимизации булевых функций. Графический метод. Метод Квайна
- Задача минимизации булевых функций. Графический метод. Метод Вейча.
- Задача минимизации булевых функций. Приложение к теории контактных схем.
- Вопросы и задачи кодирования.
- Алфавитное кодирование. Разделимая и префиксная схема кодирования, их связь.
- Алфавитное кодирование. Разделимая схема и неравенство Макмиллана, их связь.
- Кодирование с минимальной избыточностью. Минимизация длины кода.
- Цена кодирования. Оптимальное кодирование.
- Алгоритм Хаффмена, его обоснование.
- Помехоустойчивое кодирование. Кодирование с исправлением ошибок. Типы ошибок.
- Сжатие данных. Коэффициент сжатия. Сжатие текстов. Построение словаря.
- Идея адаптивного сжатия. Алгоритм Лемпела – Зива.
- Шифрование. Криптография. Понятие криптостойкости и ее оценки.
- Шифрование с помощью случайных чисел. Оценка криптостойкости.
- Шифрование с открытым ключом. Оценка криптостойкости. Цифровая подпись.
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗНАНИЙ
1. Элементы теории множеств
1. Доказать тождества:
; 
.
2. Проверить справедливость утверждений:
; 
.
3. Доказать равенства:
; 
.
4. Упростить
; 
2. Булевы функции
1. Записать СДНФ, построив таблицу истинности
; 
.
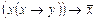2. Решить логические уравнения
; 
.
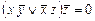3. Упростить формулы
; 
.
4. Привести к минимальной ДНФ, используя один из методов минимизации функций
; 
.
5. Построить контактные схемы, упростить их, построить упрощенные схемы
; 
.
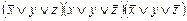6. Построить контактные схемы и проверить, равносильны ли они
4. Кодирование
1. Существует ли: а) неразделимая схема алфавитного кодирования; б) разделимая, но не префиксная схема алфавитного кодирования; в) префиксная, но неразделимая схема алфавитного кодирования, если существует привести пример, если нет, то обосновать.
2. Азбука Морзе является или нет: а) схемой алфавитного кодирования; б) разделимой схемой алфавитного кодирования; в) префиксной схемой алфавитного кодирования. Принцип работы азбуки Морзе.
3. Является ли схема алфавитного кодирования 
префиксной? Разделимой?
4. Построить оптимальное префиксное алфавитное кодирование для алфавита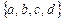 
со следующим распределением вероятностей появления букв: 
.
5. Проследить работу алгоритма Хаффмена на следующем примере распределения вероятностей появления букв алфавита:
; 
; 
.
6. Применить алгоритм сжатия Лемпела-Зива к следующему исходному тексту:
; 
; 
; 
.
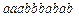Примерные варианты контрольных работ
Контрольная работа №1 по комбинаторному анализу
1. Сколько различных шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7,9 чтобы цифры не повторялись и крайние цифры были нечётными?
2. На собрании должны выступить 5 человек: А, В,С, Д и К. Сколькими способами их можно расположить в списке ораторов при условии, что В не должен выступать до того, как выступит А?
3. Сколькими способами можно переставлять буквы слова «хоровод» так, чтобы три буквы «о» не стояли рядом?
4. В разложении 
коэффициент седьмого члена разложения относится к коэффициенту пятого члена как 10:21. Найдите средний и третий члены разложения.
5. Найдите номера членов, не содержащих иррациональности в разложении 
.
6. Найдите коэффициент при 
в выражении 
.
7. Найдите число целых положительных чисел, не превосходящих 600 и не делящихся ни на одно из чисел 5, 7, 11.
