Нахождение равнодействующей 
нескольких сил 
осуществляется с помощью правил векторного сложения: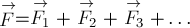 
.
Пример 2. Две силы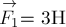 
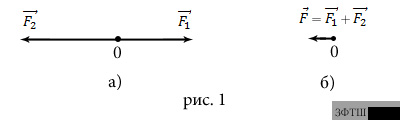
и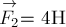 
приложены к одной точке и направлены вдоль одной прямой в противоположные стороны (рис.1а). Найдите их равнодействующую.
ОТВЕТ. Модуль равнодействующей равен разности модуле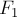й 
и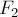 
, то есть 
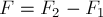. Равнодействующая приложена в той же точке и направлена в сторону большей по модулю силы 
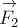(рис.1б).
Пример 3. Две силы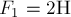 
и 
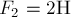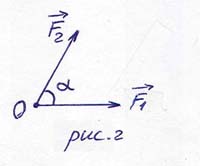
приложены к одной точке О и направлены под углом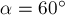 
друг к другу (рис.2). Найдите их равнодействующую.
ОТВЕТ. Согласно правилу параллелограмма, равнодействующая определяется диагональю параллелограмма, построенного на векторах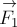 
и 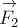как на сторонах (рис.2б). В нашем случае модуль равнодействующей найдём по теореме косинусов: 
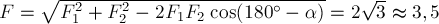Направление равнодействующей определим посредством угла 
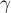, который равнодействующая составляет с одной из заданных сил, например – с 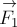. В нашем случае по теореме синусов 
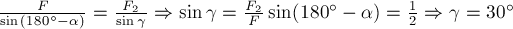. Точка приложения равнодействующей совпадает с точкой приложения исходных сил.
Замечание. Вместо правила параллелограмма при сложении двух векторов часто пользуются правилом треугольника. Для рассмотренного выше примера 4 векторный треугольник будет иметь вид, как на рис.3, и угол 
между направлениями действия сил будет являться внешним углом треугольника.
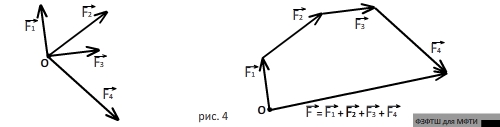
Если нужно сложить более двух сил, приложенных в одной точке, то пользуются правилом многоугольника: из конца первой силы проводят вектор, равный и параллельный второй силе; из конца второй силы – вектор, равный и параллельный третьей силе и так далее. Замыкающий вектор, проведённый из точки приложения сил к концу последней силы, по величине и направлению равен равнодействующей. На рис.4 это правило проиллюстрировано на примере нахождения равнодействующей четырёх сил , ,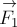 
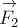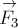и 
. Заметим, что при этом складываемые векторы не обязательно должны принадлежать одной плоскости.
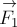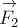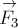Пример 4. Три одинаковые по модулю силы , и приложены к одной точке, лежат в одной плоскости и направлены под одинаковыми углами 
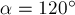попарно друг к другу (рис.5а). Найдите их равнодействующую.
ОТВЕТ. Равнодействующая этих сил равна нулю. Действуя по правилу многоугольника, получим на чертеже (рис.5б) замкнутый треугольник сил 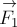, 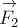и 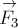, и замыкающий вектор будет нулевым.
Пример 5. Три силы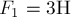 
, 
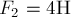и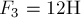 
приложены в одной точке и направлены взаимно перпендикулярно друг другу (силы 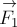и 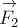лежат в горизонтальной плоскости, а сила 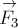направлена вертикально) (рис.6). Найдите равнодействующую.
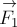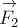ОТВЕТ. Сложение по правилу многоугольника даёт результат, изображённый на рис.6. Видим, что равнодействующая представляет собой диагональ параллелепипеда, построенного на векторах , и 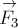как на рёбрах. Модуль равнодействующей, следовательно, равен 
. Направление равнодействующей определим с помощью углов и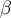 
. Из рис.6б видим, что эти углы таковы, что 
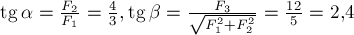. Точка приложения равнодействующей совпадает с точкой приложения исходных сил.
В ряде случаев удобнее производить сложение векторов «методом проекций».
Пример 6. Три силы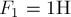 
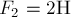, и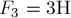 
приложены к одной точке 
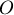, лежат в вертикальной плоскости и составляют углы 
, 
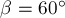и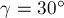 
с горизонталью соответственно (рис.7а). Найдите равнодействующую этих сил.
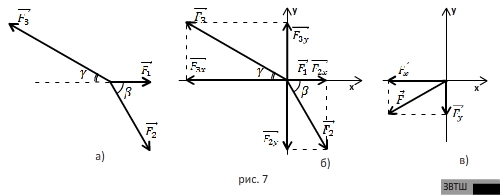
ОТВЕТ. Проведём две взаимно перпендикулярные ос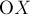и 
и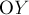 
так, чтобы ось 
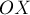совпадала с горизонталью, вдоль которой направлена сила 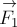. Спроецируем данные силы на оси координат (рис.7б). Проекци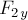и 
и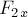 
отрицательны. Сумма проекций всех сил на оси 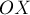равна проекции на эту ось равнодействующей 
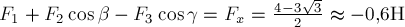. Аналогично для проекций на ось 
: 
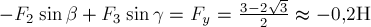. Модуль равнодействующей определяется по теореме Пифагора: 
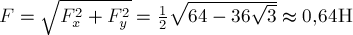. Направление равнодействующей определим с помощью угла 
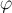, который составляет вектор равнодействующей и осью 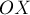(рис.7в):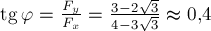 
В начало
