Линейный двусвязный список

ТЕМА 8. ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.

Одновременно с необходимостью в динамическом распределении памяти, возникла необходимость в разработке способов управления этой памятью. Если до начала работы невозможно определить, сколько памяти необходимо под переменные, то ее выделяют по мере необходимости отдельными блоками, связанными друг с другом с помощью указателей. В итоге были разработаны три основные динамические структурыобъединенные под общим термином списки.

Список — это набор динамических элементов (чаще всего структурных переменных), связанных между собой каким-либо способом. Списки бывают линейными и кольцевыми, односвязными и двусвязными, и т.д.

 

Линейный односвязный список

Линейный односвязный список представляет собой самый обыкновенный список: каждый элемент связан только с одним элементом, который называется элементом, следующим за данным. Сам элемент по отношению к следующему называется предшествующим или предыдущим. Последний элемент списка содержит. признак конца списка.

 

Элемент линейного списка как и любой динамической структуры данных представляет собой структуру, содержащую по крайней мере два поля: для хранения данных и для указателя. Поля данных могут быть любого типа: основного, составного или типа указатель. Описание простейшего элемента (компоненты, узла) выглядит следующим образом:

struct Node

{

.

. // типы данных информационных полей

.

Node *next;

};

Самыми распространенными случаями линейного односвязного списка являются очередь и стек.

Очередь — это список с таким способом связи между, элементами, при котором элементы добавляются строго в конец списка, а извлекаются строго из начала. Принцип организации списка можно описать так: "Первым пришел — первым ушел".

Ниже приведена программа, которая формирует очередь из пяти целых чисел и выводит ее на экран. Функция помещения в конец очереди называется add, а выборки — del. Указатель на начало очереди называется pbeg, указатель на конец — pend.

#include <iostream.h>

#include <conio.h>

Struct Info

{

Int i;

};

Struct FIFO

{

Info d;

FIFO *next;

};

FIFO * first(Info d); //Формирование 1 элемента очереди

void add(FIFO **pend, Info d); //Добавление элемента

Info del(FIFO **pbeg); //Удаление элемента

Void main()

{

Info d;

d.i=1;

FIFO *pbeg = first (d);

FIFO *pend = pbeg;

for (int i = 2; i<6; i++)

{

d.i=i;

add(&pend, d);

}

While (pbeg)

{

d=del(&pbeg);

cout<<d.i<<' ';

}

Getch();

}

FIFO *first(Info d) // Начальное формирование очереди

{

FIFO *pv = new FIFO;

pv->d = d;

pv->next = 0;

Return pv;

}

void add(FIFO **pend, Info d) // Добавление в конец

{

FIFO *pv = new FIFO;

pv->d = d;

pv->next = 0;

(*pend)->next = pv;

*pend = pv;

}

Info del(FIFO **pbeg) // Выборка и удаление

{

Info temp = (*pbeg)->d;

FIFO *pv = *pbeg;

*pbeg = (*pbeg)->next;

Delete pv;

Return temp;

}

Результат работы программы:

1 2 3 4 5

 

Стек — это список с таким способом связи между элементами, при котором элементы добавляются строго в начало списка и извлекаются тоже строго из начала списка. Принцип организации: "Первым пришел — последним ушел".

Ниже приведена программа, которая формирует стек из пяти целых чисел (1, 2, 3, 4, 5) и выводит его на экран Функция помещения в стек называется add, а выборки — del Указатель для работы со стеком (top) всегда ссылается на его вершину.

#include <iostream.h>

#include <conio.h>

Struct Info

{

Int i;

};

Struct LIFO

{

Info d;

LIFO *next;

};

LIFO * first(Info d); //Формирование 1 элемента стека

void add(LIFO **top, Info d); //Добавление элемента

Info del(LIFO **top); //Выборка и удаление

Int main()

{

Info d;

d.i=1;

LIFO *top = first (d);

for (int i = 2; i<6; i++)

{

d.i=i;

add(&top, d);

}

While (top)

{

d=del(&top);

cout<<d.i<<' ';

}

Getch();

Return 0;

}

LIFO *first(Info d) // Начальное формирование стека

{

LIFO *pv = new LIFO;

pv->d = d;

pv->next = 0;

Return pv;

}

void add(LIFO **top, Info d) // Добавление в конец

{

LIFO *pv = new LIFO;

pv->d = d;

pv->next = *top;

*top = pv;

}

Info del(LIFO **top) // Выборка

{

Info temp = (*top)->d;

LIFO *pv = *top;

*top = (*top)->next;

Delete pv;

Return temp;

}

 

Кольцевой список

Кольцевой список отличается от линейного тем, что в односвязном варианте элементом, следующим за последним, считается первый элемент списка; в двусвязном варианте элементом, следующим за последним, считается первый, а элементом, предшествующим первому, считается последний. Графически кольцевой список можно представить следующим образом:

Линейный двусвязный список

Линейный двусвязный список отличается от односвязного только тем, что в данном случае элемент связан не только со следующим элементом, но и с предыдущим. И первый, и последний элементы списка содержат признак конца списка. Извлечение и добавление элементов может происходить в любом месте списка.

Описание простейшего элемента:

struct Node

{

тип d; // тип данных информационного поля

Node *next;

Node *prev;

};

 

Над списками можно выполнять следующие операции:

- начальное формирование списка (создание первого элемента);

- добавление элемента в конец списка;

- чтение элемента с заданным ключом;

- вставка элемента в заданное место списка (до или после элемента с заданным ключом);

- удаление элемента с заданным ключом;

- упорядочивание списка по ключу.

Программа, которая формирует список из фамилий и например группы крови(целое число 1 2 3 или 4), добавляет запись в список, удаляет запись из списка и выводит список на экран. Указатель на начало списка обозначен рbеg, на конец списка — pend, вспомогательные указатели — pv и pkey

Указатели, которые могут измениться (например, при удалении из списка последнего элемента указатель на конец списка требуется скорректировать), передаются по адресу.

 

#include <iostream.h>

#include <conio.h>

#include<string.h>

struct info

{char fam[20];

int gr;

};

struct LIST

{

info d;

LIST *next;

LIST *prev;

};

//... -... ---.----.---- ----- -..--...-.--...-

void vvod(info &d);

LIST * first(info d); //// Формирование первого элемента

void add(LIST **pend, info d); // Добавление в конец списка

LIST * find(LIST * const pbeg, char *key); // Поиск элемента по ключу

bool remove(LIST **pbeg, LIST **pend, char *key); // Удаление элемента

LIST * insert(LIST * const pbeg, LIST **pend, char *key, info d); // Вставка элемента

void sort(LIST **pbeg, LIST **pend);

void vyvod(LIST *pbeg);

//-.... -..--..--.-.---..----.------. -----.--

int main()

{char fam[20];

info d;

int i;

vvod(d);

LIST *pbeg = first(d); // Формирование первого элемента списка

LIST *pend = pbeg; // Список заканчивается едва начавшись

// Добавление в конец списка четырех элементов 2 3 4 и 5

for (i = 0;i<3;i++)

{

vvod(d);

add(&pend,d);

}

// Вставка элемента 200 после элемента 2

vyvod(pbeg);

cout <<" posle Fam ";

cin>>fam;

vvod(d);

insert(pbeg,&pend, fam, d);

vyvod(pbeg);

// Удаление элемента 5

cout <<" Fam dla delet ";

cin>>fam;

if(!remove (&pbeg, &pend,fam)) cout<< "не найден";

vyvod(pbeg);

cout<<"do sort"<<endl;

for(i=0;i<2;i++)

{vyvod(pbeg);

if(!i){ cout<<"posle sort"<<endl;

sort(&pbeg,&pend);}}

cout<<"fam for find\n";

cin>>fam;

LIST *pv=pbeg;

do{

if(pv=find(pv,fam))

{cout << pv->d.fam<<' '<<pv->d.gr<<endl;

pv=pv->next;}

}while(pv);

return 0;

}

//... -- ---. ---- -..-..-- ---.. --..---... --

void vvod(info &d)

{cout <<"Fam"<<endl;

cin>>d.fam;

cout<<"G r"<<endl;

cin>>d.gr;

}

void vyvod(LIST *pbeg)

{LIST *pv = pbeg;

while (pv){ // вывод списка на экран

cout << pv->d.fam<<' '<<pv->d.gr<<endl;

pv = pv->next;

}}

// Формирование первого элемента

LIST * first(info d)

{

LIST *pv= new LIST;

pv->d = d;

pv->next = 0;

pv->prev = 0;

return pv;

}

//..-...-.....-...------ ---- --- --..----. --

// Добавление в конец списка

void add(LIST **pend, info d)

{

LIST *pv = new LIST;

pv->d = d;

pv->next= 0;

pv->prev = *pend;

(*pend)->next = pv;

*pend = pv;

} //-...----...----....--.---..-...-..--.......-----

// Поиск элемента по ключу

LIST * find(LIST * const pbeg, char *key)

{ LIST *pv = pbeg;

while (pv){

if(!strcmp(pv->d.fam,key))break;

pv = pv->next;

} return pv;

}

//..-----.-.....---..--.....--....------.-....----

// Удаление элемента

bool remove(LIST **pbeg, LIST **pend, char *key){

if(LIST *pkey = find(*pbeg, key)){ // 1

if (pkey == *pbeg)

{ // 2

*pbeg = (*pbeg)->next;

(*pbeg)->prev =0;

}

else if (pkey == *pend)

{ // 3

*pend = (*pend)->prev;

(*pend)->next =0;

}

else

{ // 4

(pkey->prev)->next = pkey->next;

(pkey->next)->prev = pkey->prev;

}

delete pkey;

return true; //5

}

return false; // 6

}

//..-----...------....------.......--I--......---.

// Вставка элемента

LIST * insert(LIST * const pbeg, LIST **pend, char *key, info d)

{ if(LIST *pkey = find(pbeg, key)){

LIST *pv = new LIST;

pv->d = d;

// 1 - установление связи нового узла с последующим:

pv->next = pkey->next;

// 2 - установление связи нового узла с предыдущим:

pv->prev = pkey;

// 3 - установление связи предыдущего узла с новым-

pkey->next = pv;

// 4 - установление связи последующего узла с новым

if(pkey!= *pend) (pv->next)->prev = pv;

// Обновление указателя на конец списка

// если узел вставляется в конец

else *pend = pv;

return pv;

} return 0;

}

//---------------

void sort(LIST **pbeg, LIST **pend)

{bool f;

LIST *pv,*pt,*pk=*pbeg;

while(pk)

{ pv=new LIST;

pv->d =pk->d;

pt = *pbeg;

f=true;

while (pt!=pk){ // просмотр списка

if ((pv->d).gr < (pt->d).gr){ // занести перед текущим элементом (pt)

f=false;

pv->next = pt;

if (pt == *pbeg){ // в начало списка

pv->prev = 0; *pbeg = pv;}

else{ // в середину списка

(pt->prev)->next = pv;

pv->prev = pt->prev;}

pt->prev = pv;

//запоминаем указатель на следующий элемент

pt=pk->next;

//удаляем элемент pk

if(pk==*pend)//если он стоит в конце

{(pk->prev)->next=0;

*pend=pk->prev;}

else //если он стоит в середине

{(pk->prev)->next= pk->next;

(pk->next)->prev=pk->prev;

}

delete pk;

pk=pt;

break;

} pt = pt->next;

}

if(f) pk=pk->next;

}

}

Рассмотрим подробнее функцию удаления элемента из списка remove Ее параметрами являются указатели на начало и конец списка и ключ элемента, подлежащего удалению В строке 1 выделяется память под локальный указатель pkey, которому присваивается результат выполнения функции нахождения элемента по ключу find Эта функция возвращает указатель на элемент в случае успешного поиска и 0, если элемента с таким ключом в списке нет. Если pkey получает ненулевое значение, условие в операторе i f становится истинным (элемент существует), и управление передается оператору 2, если нет — выполняется возврат из функции со значением false (оператор 6).

Удаление из списка происходит по-разному в зависимости от того, находится элемент в начале списка, в середине или в конце В операторе 2 проверяется, находится ли удаляемый элемент в начале списка — в этом случае следует скорректировать указатель pbeg на начало списка так, чтобы он указывал на следующий элемент в списке, адрес которого находится в поле next первого элемента Новый начальный элемент списка должен иметь в своем поле указателя на предыдущий элемент значение О

Если удаляемый элемент находится в конце списка (оператор 3), требуется сместить указатель pend конца списка на предыдущий элемент, адрес которого можно получить из поля prev последнего элемента Кроме того, нужно обнулить для нового последнего элемента указатель на следующий элемент Если удаление происходит из середины списка, то единственное, что надо сделать, — обеспечить двустороннюю связь предыдущего и последующего элементов После корректировки указателей память из-под элемента освобождается, и функция возвращает значение true

Работа функции вставки элемента в список проиллюстрирована на рис 3 2 Номера около стрелок соответствуют номерам операторов в комментариях.

Сортировка связанного списка заключается в изменении связей между элементами Алгоритм состоит в том, что исходный список просматривается, и каждый элемент вставляется в новый список на место, определяемое значением его ключа

 

 

Ниже приведена функция формирована упорядоченного списка (предполагается, что первый элемент существует):

 

void add_sort(Node **pbeg, Node **pend, int d)

{ Node *pv = new Node; // добавляемый элемент

pv->d = d;

Node * pt = *pbeg;

while (pt){ // просмотр списка

1f (d < pt->d){ // занести перед текущим элементом (pt)

pv->next = pt;

if (pt == *pbeg){ // в начало списка

pv->prev = О; *pbeg = pv;}

e1se{ // в середину списка

(pt->prev)->next = pv;

pv->prev = pt->prev;}

pt->prev = pv:

return;

} pt = pt->next:

}

pv->next = 0; // в конец списка

pv->prev = *pend:

(*pend)->next = pv;

*pend = pv;

}

 

 

Бинарные деревья

Бинарное дерево — это динамическая структура данных, состоящая из узлов, каждый из которых содержит, кроме данных, не более двух ссылок на различные бинарные деревья. На каждый узел имеется ровно одна ссылка. Начальный узел называется корнем дерева.

Приведем пример бинарного дерева. Узел, не имеющий поддеревьев, называется листом. Исходящие узлы называются предками, входящие — потомками. Высота дерева определяется количеством уровней, на которых располагаются его узлы.

 

Если дерево организовано таким образом, что для каждого узла все ключи его левого поддерева меньше ключа этого узла, а все ключи его правого поддерева — больше, оно называется деревом поиска. Одинаковые ключи не допускаются. В дереве поиска можно найти элемент по ключу, двигаясь от корня и переходя на левое или правое поддерево в зависимости от значения ключа в каждом узле. Такой поиск гораздо эффективнее поиска по списку, поскольку время поиска определяется высотой дерева, а она пропорциональна двоичному логарифму количества узлов.

Рассмотрим работу с бинарным деревом (в котором у каждого узла может быть только два приемника - левый и правый сын). Необходимо уметь:

построить дерево;

выполнить поиск элемента с указанным значением в узле;

удалить заданный элемент;

обойти все элементы дерева (например, чтобы над каждым из них провести некоторую операцию).

Обычно бинарное дерево строится сразу упорядоченным, т.е. узел левого сына имеет значение меньшее, чем значение родителя, а узел правого сына - большее. Например, если приходят числа 17, 18, 6, 5, 9, 23, 12, 7, 8, то построенное по ним дерево будет выглядеть так:

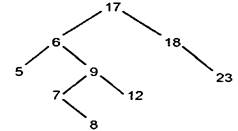
Для того, чтобы вставить новый элемент в дерево, надо найти для него место. Для этого, начиная с корня, будем сравнивать значения узлов (Y) со значением нового элемента (NEW). Если NEW < Y, то пойдем по левой ветви; в противном случае - по правой. Когда дойдем до узла, из которого не выходит нужная ветвь для дальнейшего поиска, это означает, что место под новый элемент найдено.

Путь поиска места для числа 11 покажем жирной линией.

При удалении узла из дерева возможны три ситуации:

а) исключаемый узел - лист (в этом случае надо просто удалить ссылку на данный узел);

б) из исключаемого узла выходит только одна ветвь;

в) из исключаемого узла выходят две ветви (в таком случае на место удаляемого узла надо поставить либо самый правый узел левой ветви, либо самый левый узел правой ветви для сохранения упорядоченности дерева).

Например, построенное ранее дерево после удаления узла 6 может стать таким:

Рассмотрим задачу обхода дерева. Существуют три способа обхода, которые естественно следуют из самой структуры дерева.

1) Обход слева направо: A, R, В (сначала посещаем левое поддерево, затем - корень и, наконец, правое поддерево).(5 6 7 8 9 11 12 17 18 23)

2) Обход сверху вниз: R, А, В (посещаем корень до поддеревьев).(17 6 5 9 7 8 12 11 18 23)

3) Обход снизу вверх: А, В, R (посещаем корень после поддеревьев). (5 8 7 11 12 9 6 17 23 18)

 

В качестве примера работы с древовидной структурой данных рассмотрим решение следующей задачи.

Вводятся слова; необходимо распечатать их в алфавитном порядке с указанием количества повторений каждого слова.

В программе будет использована функция der(), которая строит дерево слов, а также рекурсивная • функция для печати дерева print_der(), в которой реализован первый способ обхода дерева.

 

#include<stdio.h>

#include<conio.h>

#include<string.h>

#include<windows.h>

 

char buf[256];

char *rus(char *text)

{CharToOem(text,buf);

return buf;}

struct info

{ char *w;

int c;

};

struct TREE

{ info d;

TREE *l;

TREE *r;

};

TREE *first(char *word);//фармирование первого элемента дерева

TREE *der(TREE *kr, char *word);//добавление элемента

void print_der(TREE *kr);//просмотр элементов дерева

void main()

{ int i=0;

 

char word[40][20],ch;

puts(rus("Введите фамилии, пока не нажата клава Esc"));

scanf ("%s",word[i]);

TREE *kr=first(word[i]);

do

{

scanf("%s", word[++i]);

der(kr,word[i]);

printf("");}

while((ch=getch())!=27);

print_der(kr);

}

TREE *first(char *word)

{TREE *pv=new TREE;

(pv->d).w=word;

(pv->d).c=1;

pv->l=0;

pv->r=0;

return pv;}

TREE *der(TREE *kr, char *word)

{TREE *pv=kr,*prev;

int flag=0;

int sr;

while(pv&&!flag)

{prev=pv;

if((sr=strcmp(word, (pv->d).w))==0) {((pv->d).c)++;flag=1;}

else if(sr<0) pv= pv->l;

else pv= pv->r;}

if (flag) return pv;

// Создание нового узла

TREE *pnew=new TREE;

(pnew->d).w=word;

(pnew->d).c=1;

pnew->l=0;

pnew->r=0;

if(sr<0) prev->l= pnew;

else prev->r=pnew;

return pnew;

}

void print_der(TREE *kr)

{

if(kr)

{ print_der(kr->l);

printf(rus("Фамилия - %-20s \tКол-во повторов.- %d\n"), (kr->d).w, (kr->d).c);

print_der (kr->r);

}

}