Економічна інтерпретація математичного розв'язку

Варіант №10

ЗМІСТ

Лабораторна робота №1…………………………………………………………..3

Лабораторна робота №2…………………………………………………………..7

Лабораторна робота №3………………………………………………………....10

Лабораторна робота №4…………………………………………………………13

Лабораторна робота №5…………………………………………………………16

Лабораторна робота №6…………………………………………………………23

Лабораторна робота №9…………………………………………………………27

Лабораторна робота №11………………………………………………………..30

Лабораторна робота №12………………………………………………………..33

Лабораторна робота № 1

«Лінійна модель»

Згідно з вибіркою статистичних даних побудувати лінійну модель залежності Y від X виду:

Мета роботи:

- визначити аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів (знайти параметри моделі);

- представити модель на графіку (графічне відображення моделі засновується на побудові лінії тренду в прямокутних координатах Y-X).

Похідні дані для розрахунку моделей лабораторної роботи № 1 наведено в таблиці 1.1

Таблиця 1.1

Y	Х
6,9	10,1
10,3	9,4
12,5	6,5
12,4	5,1
13,7
16,8	4,2
19,3	3,1
20,1	2,8
21,7
25,8	1,9

 

РОЗВ’ЯЗОК

1) Визначимо аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів (знайдемо параметри моделі);

Використаємо МНК для оцінки теоретичних параметрів моделі парної регресії приводить до таких систем нормальних рівнянь:

лінійна залежність Y = a₀ + a₁X.

 

Розрахунок аналітичної залежності та параметри моделі лінійної моделі проведемо за допомогою середовища EXCEL, застосуємо для цього вбудовану функцію ЛИНЕЙН»

Результат – це оцінка параметрів лінійної регресії та регресійна статистика.

Для цього треба:

1) відмітити поле, де буде знаходитись результат розміром (k + 1) ´ 5, або m₁ ´ 5; m₁ = k + 1

2) ввійти у «майстер функцій f». У категоріях вибираємо "статистична", а в функціях – ЛИНЕЙН. Вводимо адреси значень Y, Х та значення константи і статистики;

3) для того, щоб отримати на екрані результат, натискаємо спершу клавішу F2, а потім Ctrl+Shift+Еnter.

Функція може додатково обчислювати регресійну статистику

«Відомі значення Y» — множина значень Y. Якщо масив Y має один стовпець, то кожний стовпець масиву «відомі_значення_Х» інтерпретуються як окрема змінна. Якщо масив «відомі_значення_Y» має один рядок, то кожний рядок «відомих значень Х» інтерпретується як окрема змінна.

«Відомі_значення_Х» — множина значень Х, що враховує або одну (парна регресія), або кілька змінних (множинна регресія). Якщо «відомі_значення_Х» пропустили, то вважається, що це масив {1; 2; 3;...} такого самого розміру, як n «відомих_значень Y».

«Конст» — логічне значення.

Якщо «конст» має значення «ложь», то a ₀ беруть таким, що дорівнює нулю: значення aдобирають так, щоб виконувалася рівність Y = ХА (модель без вільного члена).

Якщо «конст» має значення «истина», то a ₀ обчислюється традиційно (модель з вільним членом).

«Статистика» — логічне значення, яке вказує, чи потрібно обчислювати додаткову статистику за регресією.

Якщо «статистика» має значення «истина», то функція ЛИНЕЙН обчислює додаткову регресійну статистику у вигляді масиву.

Де а₁ - оцінка параметра; а₀ - оцінка вільного члена регресії;

Sa₁ – стандартна похибка оцінки параметра а₁;

R² - коефіцієнт детермінації;

sey – стандартна похибка залишків;

F – критерій Фішера

Ступінь свободи дорівнює (n – m), де n – кількість спостережень, m – кількість змінних у моделі; це значення необхідне для визначення табличного значення F-критерію.

Ssreg - сума квадратів відхилення, що пояснюється регресією;

ssresid – сума квадратів відхилення, що пояснюється похибкою u.

Лінійна залежність має вигляд: Y = -1,8132х+24,853.

 

Y	X	Yp
6,9	10,1	6,53947068
10,3	9,4	7,80871356
12,5	6,5	13,0670055
12,4	5,1	15,6054912
13,7		17,6000157
16,8	4,2	17,2373749
19,3	3,1	19,2318994
20,1	2,8	19,7758607
21,7		21,226424
25,8	1,9	21,4077444

 

a1	a0	-1,813204108	24,85283217
sa1	sa0	0,291859914	1,644106761
R2	sey	0,828312161	2,548540418
F	Ступінь свободи n-m	38,59619479
ssreg	ssresid	250,6845339	51,9604661

 

 

Лабораторна робота № 2. «Степенева функція»

Згідно з вибіркою статистичних даних побудувати степеневу модель залежності Y від X виду:

Мета роботи:

- визначити аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів (знайти параметри моделі);

- представити модель на графіку (графічне відображення моделі засновується на побудові лінії тренду в прямокутних координатах Y-X).

Похідні дані для розрахунку моделей лабораторної роботи № 2 наведено в таблиці 2.1

Таблиця 2.1

Y	X
30,5	46,6
	40,5
27,7	39,1
27,6	37,1
	35,5
26,6	30,9
25,5	30,7
22,4	30,1
21,6	29,7
21,5	29,4
21,3	29,3
20,1	28,8
20,1	21,7
	20,5
19,7	20,3

 

1) Визначимо аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів (знайдемо параметри моделі);

Використаємо МНК для оцінки теоретичних параметрів моделі парної регресії приводить до таких систем нормальних рівнянь:

степенева залежність

Логарифмуємо функцію lnY = ln a₁ + a₂·ln Х.

Замінюємо логарифми lnY = Y′, ln Х = Х′, ln a₁ = a′.

Одержуємо лінійну модель Y′ = a′+ a₁ · Х′.

Складаємо систему нормальних рівнянь:

 

Параметри та розрахунок регресійної статистикистепеневої функції розраховуємо за допомогою вбудованої функції «ЛИНЕЙН» (відомі_значення_Y; відомі_значення_Х; конст; статистика)

Степенева залежність має вид:

Представимо модель на графіку (графічне відображення моделі засновується на побудові лінії тренду в прямокутних координатах Y-X).

 

Y	X	LnY	lnX	Yp
30,5	46,6	3,417726684	3,841600541	36,94381531
	40,5	3,33220451	3,701301974	34,61682184
27,7	39,1	3,321432413	3,666122467	34,04352109
27,6	37,1	3,317815773	3,61361697	33,19550491
	35,5	3,295836866	3,569532696	32,49058426
26,6	30,9	3,280911216	3,430756184	30,31396085
25,5	30,7	3,238678452	3,424262655	29,46805855
22,4	30,1	3,109060959	3,404525172	29,9098211
21,6	29,7	3,072693315	3,391147046	29,70459986
21,5	29,4	3,068052935	3,380994674	29,54926577
21,3	29,3	3,058707073	3,377587516	29,49721347
20,1	28,8	3,000719815	3,360375387	29,2348589
20,1	21,7	3,000719815	3,077312261	29,2348589
	20,5	2,995732274	3,020424886	24,2606689
19,7	20,3	2,980618636	3,010620886	24,12313203

 

a2'	a1'	0,5588588	1,255875
Sa2'	Sa1'	0,0778272	0,266643
r2'	sey'	0,7986476	0,070904
F'	Ступінь свободи n-m	51,563415
ssreg'	ssresid'	0,2592313	0,065357
a2	a1	1,74867572	3,510907971

 

 

Лабораторна робота № 3. «Параболічна функція»

Згідно з вибіркою статистичних даних побудувати параболічнумодель залежності Y від X виду: .

Мета роботи:

визначити аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів (знайти параметри моделі);

представити модель на графіку (графічне відображення моделі засновується на побудові лінії тренду в прямокутних координатах Y-X).

Похідні дані для розрахунку моделей лабораторної роботи № 3 наведено в таблиці 3.1

Таблиця 3.1

Y	X

 

параболічна залежність Y = a₀ + a₁х². Замінюємо х² = х′ і отримаємо лінійну модель Y = a₀ + a₁х′.

Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:

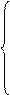
Визначимо аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів та знайдемо параметри моделі в середовище Excel за допомогою вбудованої функції ЛИНЕЙН» (відомі_значення_Y; відомі_значення_Х; конст; статистика)

 

Для того, щоб отримати на екрані результат, натискаємо спершу клавішу F2, а потім Ctrl+Shift+Еnter.

Отже, гіперболічнамодель залежності Y від X має вид:

 

Y	X	Х΄

 

 

а1	а0	0,369398	13,92977
Sa1	Sa0	0,014658	1,598136
R2	sey	0,979942	4,0357
F	Ступінь свободи n–m	635,113
ssreg	ssresid		211,7293

 

 

 

Лабораторна робота № 4. «Гіперболічна функція»

Згідно з вибіркою статистичних даних побудувати гіперболічнумодель залежності Y від X виду:

Мета роботи:

- визначити аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів (знайти параметри моделі);

- представити модель на графіку (графічне відображення моделі засновується на побудові лінії тренду в прямокутних координатах Y-X).

Похідні дані для розрахунку моделей лабораторної роботи № 4 наведено в таблиці 4.1

Таблиця 4.1

Y	X

Замінюємо і отримаємо лінійну модель Y = a₀ + a₁х′.

Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:

 

Визначимо аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів та знайдемо параметри моделі в середовище Excel за допомогою вбудованої функції ЛИНЕЙН» (відомі_значення_Y; відомі_значення_Х; конст; статистика)

 

Для того, щоб отримати на екрані результат, натискаємо спершу клавішу F2, а потім Ctrl+Shift+Еnter.

 

Отже, гіперболічнамодель залежності Y від X має вид:

Y	X	Х΄	Yp
		1,00	135,16
		0,50	84,29
		0,33	67,34
		0,25	58,86
		0,20	53,78
		0,17	50,38
		0,14	47,96
		0,13	46,15
		0,11	44,73
		0,10	43,60
		0,09	42,68
		0,08	41,91
		0,08	41,26
		0,07	40,70
		0,07	40,21

 

 

а1	а0	101,7259	33,43
Sa1	Sa0	11,33725	3,680028
r2	sey	0,860977	10,43025
F	Ступінь свободи n–m	80,50966
ssreg	ssresid	8758,661	1414,272

 

 

Лабораторна робота № 5. «Експоненціальна модель»

Згідно з вибіркою статистичних даних побудувати експоненціальнумодель залежності Y від X виду:

Мета роботи:

- визначити аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів (знайти параметри моделі);

- представити модель на графіку (графічне відображення моделі засновується на побудові лінії тренду в прямокутних координатах Y-X).

Похідні дані для розрахунку моделей лабораторної роботи № 5 наведено в таблиці 5.1

Таблиця 5.1

Y	X
18,20	1,68
18,28	1,94
18,12	3,45
15,95	4,28
14,78	4,17
14,20	4,48
14,35	4,90
9,62	7,64
8,27	8,16
6,34	7,46
6,25	6,98
5,03	6,95
4,20	8,04
2,72	9,07
1,03	9,28

Для оцінки теоретичних параметрів зводимо модель до лінійного вигляду:

Логарифмуємо функцію

Замінюємо логарифм

Одержуємо лінійну модель

Розрахунок параметрів та регресійної статистикиекспоненціальноїфункції розраховуємо за допомогою вбудованої функції «ЛИНЕЙН» (відомі_значення_Y; відомі_значення_Х; конст; статистика)

 

Y	X	LnY	Yp΄	Yp
18,2	1,68	2,901422	3,308947	27,3563
18,28	1,94	2,905808	3,234934	25,40469
18,12	3,45	2,897016	2,80509	16,52856
15,95	4,28	2,769459	2,568818	13,05039
14,78	4,17	2,693275	2,600131	13,4655
14,2	4,48	2,653242	2,511885	12,32815
14,35	4,9	2,66375	2,392326	10,93891
9,62	7,64	2,263844	1,612344	5,014551
8,27	8,16	2,112635	1,464318	4,324593
6,34	7,46	1,846879	1,663584	5,278192
6,25	6,98	1,832581	1,800223	6,050995
5,03	6,95	1,61542	1,808763	6,102891
4,2	8,04	1,435085	1,498478	4,474873
2,72	9,07	1,000632	1,205273	3,33767
1,03	9,28	0,029559	1,145493	3,143992

 

a	b	-0,28466	3,787184
Sa	Sb	0,048249	0,307416
r2	sey	0,728085	0,45008
F	Ступінь свободи n–m	34,80899
ssreg	ssresid	7,051328	2,633436

 

 

Лабораторна робота № 6
«Задача оптимального використання ресурсів»

Задача. Для виготовлення двох видів продукції А₁ і А₂ використовують три види сировини І, ІІ і ІІІ. Запаси сировини, норми їх витрат і прибуток від реалізації одиниці продукції задано у таблиці.

Знайти розмір максимального прибутку, який можна одержати за наявності даних запасів сировини.

Варіанти асортименту обрати з таблиці 6.1.

Таблиця 6.1

Затрати ресурсів на одиницю продукції	Наявність ресурсів	Прибуток
І	ІІ	ІІІ
А1	А2	А1	А2	А1	А2	І	ІІ	ІІІ	П1	П2

 

РІШЕННЯ

Позначимо кількість виготовленої продукції першого виду А₁ через х₁, другого – х₂. Враховуючи витрати сировини I, II та III виду на виготовлення одиниці продукції видів А₁ та А₂, а також обмежені запаси сировини, запишемо систему обмежень (6.1). Прибуток, одержаний з виготовлення продукції у вигляді функції мети (6.2).

(6.1)

(6.2)

 

Зведемо задачу лінійного програмування (6.3 6.4) до канонічної форми додавши невідомі х₃, х₄ та х₅ до лівої сторони двох нерівностей відповідно:

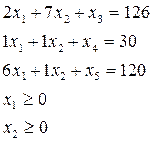(6.3)

;(6.4)

.

Розв'яжемо систему рівнянь методом Гаусса-Джордана, тому запишемо систему обмежень (6.3) у вигляді початкової розрахункової таблиці, яку назвемо ітерацією 1.

Для знаходження початкового базового плану розділимо змінні на дві групи – базові і вільні. Для вибору базових змінних доцільно скористатися таким правилом: в якості базових змінних ітерації симплекс-таблиці необхідно вибрати такі змінні (їх кількість визначається числом основних обмежень), кожна з яких тільки раз входить у рівняння основних обмежень. Решту змінних будемо вважати вільними.

Запишемо цільову форму f у вигляді рівняння

Таблиця заповнюється формально за вибраною канонічною формою.

1. Заповнюємо базові стовпчики: на перетині однойменних рядків і стовпчиків ставимо 1, а в усіх інших клітинках будуть нулі.

2. В інших рядках виписуємо коефіцієнти, що стоять біля відповідних невідомих. Нульовий рядок відповідає оптимізуючій формі і служить для визначення ступеня оптимальності опорного плану.

Ітерація 1

Базові невідомі	План (опорний розв'язок)	x1	x2	x3	x4	x5	min
x3		2,00	7,00	1,00	0,00	0,00
x4		1,00	1,00	0,00	1,00	0,00
x5		6,00	1,00	0,00	0,00	1,00
F(X0)		-20,00	-15,00	0,00	0,00	0,00

Критерій оптимальності. Якщо задача максимізується і в нульовому рядку відсутні від'ємні числа (за винятком хіба що стовпчика "опорний розв'язок (план)"), то опорний план є оптимальним (при мінімізації задачі для оптимальності плану достатньо відсутності додатних чисел у нульовому рядку, за винятком, можливо, опорного розв'язку).

Коефіцієнт рядка "5" можна інтерпретувати як приріст функції f при збільшенні вільної невідомої на одиницю. Приріст буде додатним, якщо коефіцієнт від'ємний, і від'ємним – якщо коефіцієнт додатний.

В нашому випадку є два від'ємні числа (–20), (–15), беремо найбільше за модулем від'ємне число (–20) (при мінімізації задачі – найбільше додатне), тоді стовпчик "х1" будемо називати ключовим стовпчиком.

Для вибору ключового елемента складаємо відношення вільних членів (чисел стовпчика "опорний розв'язок") до відповідних додатних чисел ключового стовпчика (усі інші відношення будемо вважати рівними нескінченності)

Перше відношення менше, тому число (2) першого рядка буде ключовим елементом. Ключовий елемент в таблиці позначаємо рамкою і переходимо до другої ітерації.

Ітерація 2

Базові невідомі	План (опорний розв'язок)	x1	x2	x3	x4	x5	min
x1		1,00	3,50	0,50	0,00	0,00
x4	-33	0,00	-2,50	-0,50	1,00	0,00
x5	-258	0,00	-20,00	-3,00	0,00	1,00
F(X1)		0,00	55,00	10,00	0,00	0,00

 

Послідовність заповнення другої та наступних ітерацій така (використовуємо метод Гаусса-Жордана):

Замість базової невідомої х₃ (ключовий рядок), вводимо нову базову невідому х₁ (невідому ключового стовпчика),

Формально заповнюємо базові стовпчики (пункт 1 ітерації 1).

Ключовий рядок одержуємо від ділення його елементів попередньої ітерації на ключовий елемент.

Усі інші комірки ітерації заповнюємо за правилом прямокутника:

Усі інші комірки ітерації заповнюємо за правилом прямокутника:

де a_ij', b_i ' відповідно шукані елементи нової ітерації, а а_ij, b_i – попередньої, а_qs – ключовий елемент.

Ітерація 3

Базові невідомі	План (опорний розв'язок)	x1	x2	x3	x4	x5	min
x1		1,00	0,00	-0,20	1,40	0,00	-84
x2		0,00	1,00	0,20	-0,40	0,00
x5		0,00	0,00	1,00	-8,00	1,00
F(X2)		0,00	0,00	-1,00	22,00	0,00

Ітерація 4

Базові невідомі	План (опорний розв'язок)	x1	x2	x3	x4	x5
x1					-0,20	0,20
x2					1,20	-0,20
x3					-8,00	1,00
F(X3)					14,00	1,00

 

В рядку 5 вже немає від'ємних чисел, тому опорний план останньої таблиці оптимальний і виписуємо його із стовпчика "опорний розв'язок" x₁=18, x₂=12 Fmax=20*18+15*12=540

Економічна інтерпретація математичного розв'язку.

Аналіз системи обмежень і цільової функції показує, що подальше збільшення прибутку неможливе, розв'язок є оптимальний, найбільший прибуток при даних запасах сировини становить f _max =540 одиниць, а об'єми виготовленої продукції видів А₁ і А₂ дорівнюють відповідно 18 та 12 одиниць.

Лабораторна робота № 9

«Оптимізація виробничої програми ковбасного виробництва»

 

У табл. 9.1 дані асортимент виробів, що випускаються в розрізі основних показників роботи підприємства.

Побудувати модель оптимальної річної програми підприємства в загальному, табличному та аналітичному вигляді за критерієм оптимізації – максимум прибутку.

Розрахувати обсяг ресурсів на свій асортимент, який задається варіантом.

Побудувати матрицю коефіцієнтів.

Виконати розв’язання задачі на ПК.

Виконати економічний аналіз отриманих результатів.

Таблиця 9.1

Вихідні дані для оптимізації ковбасного виробництва

Асортимент продукції, найменування ковбаси	Норми витрат сировини, т/т	Оптова ціна 1 тонни, грн..	Собівартість 1 тонни, грн	Трудоміскість 1 тонни люд./ год.	Норми часу роботи обладнання, год./т	Попит
яловичина	свинина	min	max
1.Лікарська	0,7	0,25			57,5	3,8
2.Чайна	0,7	0,25			57,5	3,8
3.Сосиски яловичі	0,7	0,25			55,5	5,2
4.Сардельки яловичі	0,7	0,25			55,7	5,2

 

Наявність на підприємстві ресурсів така: яловичини – 2000 т; свинини – 750 т; загальна трудомісткість – 190000 люд-год.; час роботи обладнання – 20000 год. на рік.

Розв’язок

Спочатку побудуємо математичну модель задачі, для цього визначимо спочатку змінні: X_j – випуск продукції j-того виду. В даній моделі чотири змінні Х₁, Х₂, Х₃ і Х₄ – це відповідно випуск ковбас «Лікарська», «Чайна», «Сосиски яловичі» і «Сардельки яловичі».

Для того, щоб побудувати функцію цілі – максимум річного прибутку – потрібно визначити прибуток з виробітку 1 т всіх видів продукції:

«Лікарська»: 4870 – 4320 = 550 грн.;

«Чайна»: 3320 – 3010 = 310 грн.;

«Сосиски яловичі»: 4050 – 3800 = 250 грн.;

«Сардельки яловичі»: 4240 – 3970= 270 грн.

Функція цілі максимум прибутку запишеться так:

F(x) = 550Х₁ + 310Х₂ + 250Х₃ + 270Х₄ ® max

Обмеження задачі:

– за яловичиною:

0,7Х₁ + 0,7Х₂ + 0,7Х₃ + 0,7Х₄ £ 2000;

– за свининою:

0,25Х₁ + 0,25Х₂ + 0,25Х₃ + 0,25Х₄ £ 750;

– за трудомісткістю:

57,5Х₁ + 57,5Х₂ + 55,5Х₃ + 55,7Х₄ £ 190000;

– за часом роботи обладнання:

3,8Х₁ + 3,8Х₂ + 5,2Х₃ + 5,2Х₄ £ 20000;

– за попитом:

Х₁£900; Х₂£500; Х₃£500; Х₄£1600;

Х₁³600; Х₂³300; Х₃³400; Х₄³120;

– умова невід’ємності даних:

Х₁, Х₂, Х₃, Х₄ ³ 0.

Вирішуємо задачу за допомогою симплекс-методу в Excel з використанням інструменту «Пошук рішення» в меню «Сервіс» (рис. 9.1).

Рис. 9.1

Отримали таке рішення задачі: Х₁=900 т; Х₂=500 т; Х₃=500 т; Х₄=160 т.

Таблиця 9.2

Економічна ефективність оптимального рішення

Найменування показника	Значення показника	Відхилення
До оптимізації	Після оптимізації	Абсолютне	Відносне
1. Випуск продукції, т
1.Сосиски яловичі
2.Сосиски шкільні
3.Сардельки яловичі
4.Одеська п/к			40,00
2. Вартість випущеної продукції, грн.				144,65
3. Вартість витрат на випущену продукцію, грн.				144,37
4. Прибуток, грн.
5. Рентабельність продукції, %	10,11	10,32	0,21
6. Витрати на одиницю продукції, грн.	0,9081	0,9065	-0,0017	99,81
7. Використання ресурсів:
– яловичина, т			-558
– свинина, т			-235
– трудомісткість, люд-год.			-72838
– час роботи обладнання, год.			-11248

 

Після того як рішення отримано, потрібно надрукувати звіт про результати. Звіт про результати – це один із варіантів подання рішення задачі за допомогою інструменту «Пошук рішення» в меню «Сервіс».

Проведемо аналіз результатів за допомогою табл. 9.2.

Вартість продукції до і після оптимізації розраховуємо, як суму добутків ціни 1 т і відповідної кількості продукції до і після оптимізації. Аналогічно розраховуємо собівартість випуску продукції до і після оптимізації як суму добутків собівартості 1 т продукції і відповідної кількості продукції до і після оптимізації.