а) по горизонтальной проекции прямых
б) по фронтальной проекции прямых
в) необходимо выполнить дополнительные построения
38. Методом конкурирующих точек определить видимость прямых АС и ДБ:
а) АС – видимая; ВД – невидимая
б) АС – невидимая; ВД – видимая
в) АС и ВД – невидимые
 |
39.Какие из заданных точек принадлежат поверхности конуса?
a) точки А и В
b) точка В
c) точка C
d) точки А и С
e) точка А
40. Какие из заданных точек принадлежат поверхности пирамиды? 
1) точка А
2) точки А и В
3) точка C
4) точка В
5) точки А и С
41.Определить на каком из рисунков прямая перпендикулярна плоскости α?
а)
б)
в)
а) б) в)
42.Какие из заданных точек принадлежат поверхности сферы?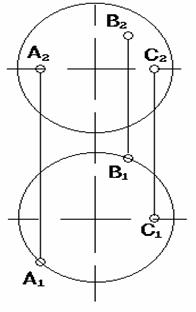 
a) точка А
b) точка В
c) точки А и В
d) точка C
e) точки А и С
43. Какие плоскости не применяют в качестве вспомогательных при построении фигур плоских сечений?
а) плоскости уровня;
б) проецирующие плоскости;
в) общего положения
44. От какой плоскости в сечении конуса получится гипербола? 
1) плоскостью 
2) плоскостью 
3) плоскостью 
4) плоскостью 
5) плоскостью 
45. На каком рисунке плоскости взаимно перпендикулярны?
а)
б)
в)
|
а) б) в)
46. Главная линия плоскости это:
а) прямая частного положения, лежащая в этой плоскости и одна из ее
проекций параллельна одноименному следу
б) любая прямая, лежащая в данной плоскости и одна из ее проекции параллельна одноименному следу
в) прямая перпендикулярная данной плоскости
47. Плоскости в пространстве параллельны, если:
а) две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости
б) прямая одной плоскости параллельна прямой другой плоскости
в)две пересекающиеся прямые параллельны прямой другой плоскости
33.При пересечении цилиндра какой плоскостью (плоскостями) в сечении получается эллипс?
1) плоскостями 
и 
2) плоскостью 
и плоскостью
3) плоскостью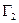 
и плоскостью
48.Установить правильный алгоритм решения задачи: «Нахождение расстояния от точки до плоскости»
1- в плоскости выделить линии уровня
2- опустить перпендикуляр на плоскость к натуральной величине отрезка
3- заключить прямую (перпендикуляр) в плоскость
4- найти линию пересечения двух плоскостей
5- указать точку встречи
6- определить натуральную величину отрезка
49. Сколько раз заменяют плоскость проекций, чтобы прямую общего положения спроецировать в точку?
а) один раз
б) два раза
в) три раза
50.Задать цилиндрическую поверхность можно:
А)
б)
в)
г)
51.Не является циклической поверхностью:
а) цилиндр
б) винтовая поверхность
в) конус
г) сфера
52. Оси стандартной прямоугольной диметрии изображены на рисунке:
а)
б)
в)
+г)
53. Малая ось эллипса в плоскости X, Y расположена к оси Хна под углом:
а) 60
б) 90
в) 30
г) 120
54.Две пересекающиеся плоскости показаны на рисунке:
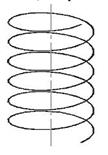
а)
б)
в)
г)
55. На приведенном рисунке плоскость __________пересекает конус по параболе?
а) А
б) Д
в) Г
г) В
56. На каких чертежах изображены плоскости параллельные профильной плоскости проекции?
а)
б)
в)
Г)
+д)
57. Плоскими кривыми являются:
а) цилиндрическая винтовая
б) коническая винтовая
в) парабола
г) окружность
58. Точка А принадлежит прямой на чертеже:
а)
б)
в)
г)
59. Плоскость на чертеже НЕЛЬЗЯ задать:
а) проекциями пересекающихся прямых
б) проекциями скрещивающихся прямых
в) проекциями треугольника
г) проекциями параллельных прямых
60.Проецирование называют ортогональным, если проецирующие лучи:
а) не параллельны между собой
б) проходят через одну точку
в) перпендикулярны плоскости проекций
г) проходят под острым углом к плоскости проекций
61. Требуется привести треугольник в проецирующее положение, для этого ось Х1 дополнительной плоскости проекции следует провести:
а)┴А1Е1
б) ┴А2С2
в) ┴С2В2
г)┴А2Е2
62.Прямая m пересекает заданную плоскость под прямым углом, на рисунках:
а)
б)
в)
г)
63.На рисунке изображена развертка:
а)прямого кругового конуса
б)цилиндра
в) сферы
г) тора
64.Призма изображена на рисунке:
а)
б)
в)
г)
д)
65.Плоскость можно задать:
а) одной прямой
б) тремя прямыми
в) двумя пересекающимися прямыми
г) тремя точками, не лежащими на одной прямой
66. Диметрией называют аксонометрическую проекцию, у которой показатели искажения _________ осям:
а) одинаковые по всем
б) переменные по всем
в) одинаковые по двум
г) разные по всем
67. Пирамида с основанием в виде квадрата, лежащего в плоскости ХОУ, построенная в прямоугольной изометрии, изображена на рисунке:
а) А
б) Б
в) В
г) Г
68.Аксонометрическая проекция, у которой коэффициенты искажения по всем осям равны, а углы между аксонометрическими осями расположены под углом 120, называют______проекцией:
а) горизонтальной изометрической
б) фронтальной изометрической
в) прямоугольной изометрической
г) фронтальной косоугольной диметрической
69. Для построения линии пересечения поверхностей, в данном случае, необходимо использовать:
а) способ эксцентрических сфер
б) способ концентрических сфер
в) способ секущих плоскостей
г) любой способ
70. Укажите рисунок, на котором правильно определено точка пересечения прямой с плоскостью:
а)
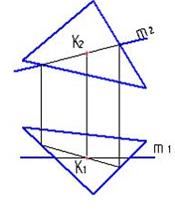
б)
в)
г)
71. Заданной поверхности принадлежит точка:
а) Д
б) С
в) А
г) В
72. Способ вращения вокруг проецирующей прямой заключается во вращении точек геометрического объекта в пространстве вокруг прямой, _________ одной из плоскостей проекций:
а) наклоненной под углом 45 к
б) наклоненной под углом 60 к
в) перпендикулярной
г) параллельной
73. Натуральная величина отрезка на рисунке определена методом:
а) вращением вокруг горизонтали
б) вращением вокруг фронтально-проецирующей прямой
в) замены плоскостей проекций
г) вращением вокруг горизонтально-проецирующей прямой
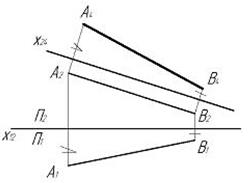
74. Угол наклона отрезка АВ к плоскости П2 указан на рисунке цифрой:
а) 1
б) 2
в) 3
г) 4
75. Плоскости Г и Σ пересекаются НЕ под прямым углом:
а)
б)
в)
+г)
76. Точка пресечения прямой с горизонтальной плоскостью проекций показана на рисунке:
а)
б)
в)
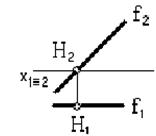
г)
77. Поверхность, изображенная на чертеже, называется:
а) конической
б)винтовой
в) тором
г) линейчатой
78. Чертеж представляет собой развертку правильной:
а) треугольной призмы
б) четырехугольной пирамиды
в) пятиугольной пирамиды
г) шестиугольной пирамиды
79. Аксонометрические проекции – это проекции построенные:
а) методом центрального проецирования на несколько плоскостей проекций
б) методом центрального проецирования
в) методом ортогонального проецирования на несколько плоскостей проекций
+г) методом параллельного проецирования на несколько плоскостей проекций
80. Прямоугольной изометрической проекцией окружности, параллельной одной из плоскостей проекций, является:
а) окружность
б) эллипс
в) линия
г) овал
81.Натуральная величина отрезка АВ (обозначена А4В4) построена правильно на чертеже:
а) Г
б) А
в) Б
г) В
82. Натуральная величина угла наклона прямой АВ к плоскости П1 указана цифрой:
а) 1
б) 2
в) 3
г) 4
83. Способ вращения вокруг фронтально-проецирующей прямой, на данном рисунке, позволяет:
а) получить натуральную величину отрезка прямой общего положения на горизонтальной плоскости проекций
б) определить угол наклона прямой общего положения к фронтальной плоскости проекции
в) получить натуральную величину отрезка прямой общего положения на фронтальной плоскости проекций
г) определить угол наклона прямой общего положения к горизонтальной плоскости проекции
84.Прямая линия на чертеже задается проекциями:
а) трех точек
б) двух точек
в) отрезка прямой
г) четырех точек
85. На рисунке показано преобразование проецирующей плоскости в плоскость уровня, выполненное способом:
а) вращения вокруг прямой уровня
б) вращения вокруг проецирующей прямой
в) плоскопараллельного перемещения
г) замены плоскостей проекций
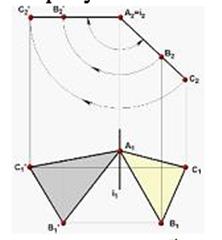
86. На рисунке изображена приближенная развертка:
а) тора
б) сферы
в) прямого кругового конуса
г) цилиндра
87. К поверхности второго порядка относятся:
а) плоскость
б) цилиндрическая поверхность вращения
в) открытый тор
г) коническая поверхность вращения
88.Если ось цилиндра, на котором расположена винтовая линия, перпендикулярна плоскости проекции, то винтовая линия на эту плоскость проецируется в:
а) эллипс
б) окружность
в) синусоиду
г) параболу
89.Гипербола изображена на рисунке:
а) Б
б) Г
в) А
г) В
90. Прямая и плоскость треугольника (АВС):
а) параллельны
б) пересекаются
в) скрещиваются
г) совпадают
91. Эллипсы, изображающие окружность, лежащие в плоскостях, параллельных плоскостям проекций, в прямоугольной изометрии правильно показаны на рисунке:
а) А
б) В
в) Б
92. Фронтальный след прямой – это точка ее пересечения с …… плоскостью проекций:
а) фронтальной
б) горизонтальной
в) профильной
г) дополнительной
93.На П1 прямой угол проецируется в прямой, если одна сторона угла является …., а другая – прямой общего положения:
а) проецирующей прямой
б) фронталью
в) горизонталью
г) профильной прямой уровня
94. Фигура развертки боковой поверхности цилиндра, изображенного на рисунке, представляет собой:
а) круговой сектор (сегмент)
б) плоскость, ограниченную прямоугольником
в) круг
г) плоскость, ограниченную эллипсом
95.Горизонтальной проекцией цилиндрической винтовой линии, изображенной на рисунке, является:
а)эллипс
б)синусоида
в)окружность
г) парабола
96. Прямая n, параллельная плоскости треугольника (АВС), изображена на рисунке:
а)
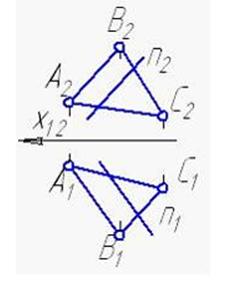
б)
в)
г)
97.Коэффициент искажения по оси ОУ вычисляется по формуле:
а)
б)
в)
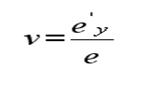
г)
98.Способ преобразования чертежа, при котором геометрический объект перемещается в пространстве, называется способом:
а) замены плоскостей проекций
б)дополнительного проецирования
в)параллельного проецирования
г)вращения вокруг проецирующей прямой
