К базовым линейным операциям, из которых могут быть сформированы любые линейные операторы преобразования, относятся операции скалярного умножения, сдвига и сложения сигналов:
y(t) = b ´ x(t), y(t) = x(t-t), y(t) = a(t)+b(t).
Рис. 11.1.1. Графика системных операций
|
Операции сложения и умножения являются линейными только для дискретных и аналоговых сигналов.
Для систем, с размерностью 2 и более существует также еще одна базовая операция, которая называется операцией пространственного маскирования, которая может рассматриваться как обобщение скалярного умножения. Так, для двумерных систем:
z(x,y) = c(x,y)×u(x,y),
где u(x,y) – двумерный входной сигнал, c(x,y) – пространственная маска постоянных (весовых) коэффициентов. Пространственное маскирование представляет собой поэлементное произведение значений сигнала с коэффициентами маски.
Дифференциальные уравнения как универсальный инструмент изучения сигналов
Дифференциальные уравнения представляют собой универсальный инструмент задания определенной связи между сигналами входа и выхода, как в одномерных, так и в многомерных системах, и могут описывать систему, как в режиме реального времени, так и апостериорно. Так, в аналоговой одномерной линейной системе такая связь обычно выражается линейным дифференциальным уравнением:
am 
= 
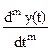bn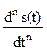 
. (11.1.1)
При нормировке к ао = 1, отсюда следует:
y(t) = 
bn 
– 
am 
. (11.1.1')
По существу, правой частью этого выражения в самой общей математической форме отображается содержание операции преобразования входного сигнала, т.е. задается оператор трансформации входного сигнала в выходной. Для однозначного решения уравнений (11.1.1) кроме входного сигнала s(t) должны задаваться определенные начальные условия, например, значения решения y(0) и его производной y'(0) по времени в начальный момент времени.
Аналогичная связь в цифровой системе описывается разностными уравнениями:
am y((k-m)t) = bn s((k-n)t). (11.1.2)
y(kt) = bn s((k-n)t) – am y((k-m)t). (11.1.2')
Последнее уравнение можно рассматривать как алгоритм последовательного вычисления значений y(kt), k = 0, 1, 2, …, по значениям входного сигнала s(kt) и предыдущих вычисленных значений y(kt) при известных значениях коэффициентов am, bn и с учетом задания начальных условий - значений s(kt) и y(kt) при k < 0. Интервал дискретизации в цифровых последовательностях отсчетов обычно принимается равным 1, т.к. выполняет только роль масштабного множителя.
Рекурсивные системы
На практике стремятся упростить системы взаимозависимых моделей и привести их к так называемому рекурсивному виду. Для этого сначала выбирают эндогенную переменную (внутренний показатель), зависящую только от экзогенных переменных (внешних факторов), обозначают ее у1. Затем выбирается внутренний показатель, который зависит только от внешних факторов и от y1, и т.д.; таким образом, каждый последующий показатель зависит только от внешних факторов и от внутренних предыдущих. Такие системы называются рекурсивными. Параметры первого уравнения рекурсивных систем находят методом наименьших квадратов, их подставляют во второе уравнение и опять применяется метод наименьших квадратов, и т.д.
