ЛАБОРАТОРНАЯ РАБОТА МАТЕМАТИЧЕСКИЙ МАЯТНИК
Цель работы: ознакомиться с одним из методов определения ускорения свободного падения.
Оборудование: ЛКМ-2 (математический маятник с отверстиями, пластмассовый фиксатор, измерительная система ИСМ-2).
Краткие теоретические сведения
Математический маятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения.
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа (циклическая частота колебаний), определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах. Уравнение малых колебаний маятника около нижнего положения равновесия (гармоническое уравнение) имеет вид:
.
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным дифференциальным уравнением второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, 
— начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями.
Период малых собственных колебаний математического маятника длины 
неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения 
равен
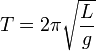
и не зависит от амплитуды колебаний и массы маятника.
Исходя из теории колебаний математического маятника, измеряя период его колебаний и длину подвеса, можно определить ускорение свободного падения.
Порядок выполнения работы
1. Установить математический маятник на шкиве стойки.
2. В случае, если маятник представляет собой стержень с грузиком на одном из его концов, для устранения паразитных колебаний на ось шкива надеть пластмассовую втулку-фиксатор, прижимающую стержень к шкиву.
3. Установить на измерительной системе ИСМ-2 тумблеры: «0,1мс/мс/0,01мс» в положение «мс» (измерение времени с точностью до 1 мс), «1/2» в положение «1», «однокр/цикл» в положение «однокр». Обнуление счетчика и подготовка его к измерению времени производится кнопкой «готов».
4. Измерить период колебаний. Для этого в каждом положении маятника 3 раза измерить время 5 колебаний – t 5, найти среднее значение времени и затем определить период колебаний. Для измерения времени 5 колебаний нужно:
– отклонить маятник от вертикали на небольшой угол;
– отпуская маятник, одновременно нажать кнопку «ручн»;
– после истечения 5 колебаний вновь нажать кнопку «ручн». Счетчик покажет время 5 колебаний в миллисекундах;
– для проведения повторного опыта счетчик обнулить кнопкой «готов».
5. Выполнить измерения для маятников трёх различных масс и длин подвеса. Получить 5 результатов. Результаты занести в таблицу 1.
Таблица 1. Результаты измерений ускорения свободного падения.
| № п.п. | Масса грузика, г | Длина подвеса, м | t 5, мс | Период колебаний Т, мс | g, м/с2 | < g >- gi, м/с2 | (< g >- gi)2, (м/с2)2 |
| Сумма | |||||||
| Среднее |
6. Произвести статистическую обработку полученных результатов, определив среднее значение < g >, абсолютную погрешность D g (по формуле Стьюдента) и относительную погрешность e.
Результат представить в виде:
g = (< g > ± D g) (ед. изм.), при a = 0.95, e = %
7. Сравнить полученные значения с табличным.
