3.1. Математическое ожидание дискретной случайной величины
Закон (ряд) распределения дискретной случайной величины дает исчерпывающую информацию о ней, так как позволяет вычислить вероятности любых событий, связанных со случайной величиной. Однако такой закон (ряд) распределения бывает трудно обозримым, не всегда удобным (и даже необходимым) для анализа. Рассмотрим, например, задачу.
Задача. Известны законы распределения случайных величин Х и Y— числа очков, выбиваемых 1-ми 2-м стрелками.

Необходимо выяснить, какой из двух стрелков стреляет лучше. Рассматривая ряды распределения случайных величин X и Y, ответить на этот вопрос далеко не просто из-за обилия числовых значений. К тому же у первого стрелка достаточно большие вероятности (например, больше 0,1) имеют крайние значения числа выбиваемых очков (Х= 0; 1 и X=9; 10), а у второго стрелка — промежуточные значения (Y= 4; 5; 6) (см. многоугольники распределения вероятностей Х и Y на рис. 3).
Очевидно, что из двух стрелков лучше стреляет тот, кто в среднем выбивает большее количество очков.

Рис.3
Таким средним значением случайной величины является ее математическое ожидание.
Определение. Математическим ожиданием, или средним значением, М(Х) дискретной случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:

Пример. Вычислить М(Х) и М(Y) в задаче о стрелках. Решение. По формуле (3.3)

т.е. среднее число выбиваемых очков у двух стрелков одинаковое.
Обратим внимание на механическую интерпретацию математического ожидания. Если предположить, что каждая материальная точка с абсциссой хi имеет массу, равную Pi (i = 1,2,...,n), а вся единичная масса распределена

между этими точками, то математическое ожидание представляет собой абсциссу центра масс системы материальных точек. Так, для систем материальных точек, соответствующим распределениям X и Y примера, центры масс совпадают: М(Х) =М(Y) =5,36.
Если дискретная случайная величина X принимает бесконечное, но счетное множество значений х1, х2,...,хn, то математическим ожиданием, или средним значением, такой дискретной случайной величины называется сумма ряда (если он абсолютно сходится):
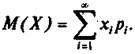
Так как ряд может и расходиться, то соответствующая случайная величина может и не иметь математического ожидания. Например, случайная величина X с рядом распределения

не имеет математического ожидания, ибо сумма ряда

равна ¥. На практике, как правило, множество возможных значений случайной величины распространяется лишь на ограниченный участок оси абсцисс и, значит, математическое ожидание существует.
Рассмотрим свойства математического ожидания.
1. Математическое ожидание постоянной величины равно самой постоянной:

2. Постоянный множитель можно выносить за знак математического ожидания, т.е.

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е.

4. Математическое ожидание произведения конечного числа случайных величин равно произведению их математических ожиданий, т.е.
М(ХY)=M(X)M(Y)
5. Если все значения случайной величины увеличить (уменьшить) на постоянную С, то на эту же постоянную С увеличится (уменьшится) математическое ожидание этой случайной величины
М(Х±С)=М(Х)±С
ПРИМЕР Найти математическое ожидание случайной величины Z=8X-5Y+7, если известно, что М(Х)=3, М(Y)=2
Решение Используя свойства 1,2,3 математического ожидания, найдем M(Z)=8M(X)-5M(Y)+7=8*3-5*2+7=21
3.2. Дисперсия дискретной случайной величины
Только математическое ожидание не может в достаточной степени охарактеризовать случайную величину. В задаче о стрелках, мы убедились в том, что среднее количество выбиваемых очков у двух стрелков одинаковое. Но если у первого стрелка значительные вероятности имеют крайние значения, сильно отличающиеся от среднего, то у второго стрелка наоборот – значения, близкие к среднему. Очевидно, что лучше стреляет тот стрелок, у которого при равенстве числа средних значений выбитых очков, меньше отклонения (разброс, рассеяние) этого числа относительно среднего значения.
В качестве такой характеристики рассматривается дисперсия случайной величины. Слово дисперсия означает рассеяние.
ОПРЕДЕЛЕНИЕ: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
D(X)=M[X-M(X)]2
Если случайная величина X — дискретная с конечным числом значений, то
 ,
,
где а=М(Х)
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину 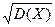 .
.
Определение. Средним квадратическим отклонением (стандартным отклонением или стандартом) sх случайной величины X называется арифметическое значение корня квадратного из ее дисперсии:
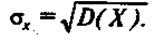
Пример В задаче о стрелках вычислить дисперсию и среднее квадратическое отклонение числа выбитых очков для каждого стрелка.
Решение. Ранее были вычислены М(Х)=5,36 и M(Y)=5,36. По формуле:

Итак, при равенстве средних значений числа выбиваемых очков (M(X)=M(Y)) его дисперсия, т.е. характеристика рассеяния относительно среднего значения, меньше у второго стрелка и, очевидно, ему для получения более высоких результатов стрельбы по сравнению с первым стрелком нужно сместить «центр» распределения числа выбиваемых очков, т.е. увеличить M(Y), научившись лучше целиться в мишень.
Отметим свойства дисперсии случайной величины.
1. Дисперсия постоянной величины равна нулю:

2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

Это свойство часто используют при вычислении дисперсии. Вычисление по данной формуле дает, например, упрощение расчетов по сравнению с основной формулой, если значения xi случайной величины — целые, а математическое ожидание, а значит и разности (хi-а) — нецелые числа.
4. Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий:

Обратим внимание на то, что дисперсия как суммы, так и разности независимых случайных величин равна сумме их дисперсий.
Пример. Найти дисперсию случайной величины Z =8X—5Y+7, если известно, что случайные величины Х и Y независимы и D(X) =1,5, D(Y) =1.
Решение. Используя свойства 1, 2, 4 дисперсии, найдем

Математическое ожидание, дисперсия, среднее квадратическое отклонение и другие числа, призванные в сжатой форме выразить наиболее существенные черты распределения, называются числовыми характеристиками случайной величины. Обращаем внимание на то, что сама величина X — случайная, а ее числовые характеристики являются величинами неслучайными, постоянными.
3.3 Функция распределения случайной величины
До сих пор в качестве исчерпывающего описания дискретной случайной величины мы рассматривали закон ее распределения, представляющий собой ряд распределения или формулу, позволяющие находить вероятности любых значений случайной величины X. Однако такое описание случайной величины X не является единственным, а, главное, не универсально. Так, оно неприменимо для непрерывной случайной величины, так как, во-первых, нельзя перечислить все бесконечное несчетное множество ее значений; во-вторых, как мы увидим дальше, вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю.
Для описания закона распределения случайной величины Х возможен и другой подход: рассматривать не вероятности событий, Х=х для разных х (как это имеет место в ряде распределения), а вероятности события Х<х, где х — текущая переменная Вероятность Р(Х<х), очевидно, зависит от х, т.е. является некоторой функцией от х.
Определение. Функцией распределения случайной величины X называется функция F(x), выражающая для каждого х вероятность того, что случайная величина X примет значение меньшее х:

Функцию F(x) иногда называют интегральной функцией распределения или интегральным законом распределения.
Пример. Дан ряд распределения случайной величины

Найти и изобразить графически ее функцию распределения.
Решение. Будем задавать различные значения х и находить для них F(x) = Р(Х,< х).
1. Если х < 1, то, очевидно, F(x) = 0 (в том числе и при х=l F(1)=P(x<l) = 0);
2. Пусть 1 < х £4 (например, х=2);
F(x) = Р(Х = 1) = 0,4. Очевидно, что и F(4) = Р(Х < 4) = 0,4.
3. Пусть 4 < х £ 5 (например, х=4,25);
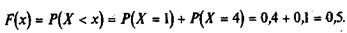


Этот пример позволяет прийти к утверждению, что функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции F(x) равна 1.
Рассмотрим общие свойства функции распределения.
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей'.
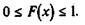
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
3. На минус бесконечности функция распределения равна нулю, а на плюс бесконечности равна единице, т.е.

4. Вероятность попадания случайной величины в интервал [х1,x2) равна приращению ее функции распределения на этом интервале, т.е.

Пример Функция распределения случайной величины X имеет вид:

Найти вероятность того, что случайная величина примет значение в интервале [1;3).Решение. По формуле







