Расчет среднего уровня ряда
1. Интервальный ряд. Пример: имеются данные об объеме выпуска продукции за несколько месяцев:
| Месяц | Объем продукции, т |
| Январь | |
| Февраль | |
| Март | |
| Апрель |
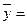
2. Дискретный ряд с равноотстоящими датами. Используется формула средней хронологической
Пример: Имеются данные о числе сотрудников организации на начало месяца.
| Дата | № | 
|
| 01.янв | ||
| 01.фев | ||
| 01.мар | ||
| 01.апр |
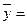
3. Дискретный ряд с неравноотстоящими датами:
,
где 
-- промежуток времени, в течение сохранялся уровень ряда .
Пример: малое предприятие открылось 10.11.13. На момент открытия в нем работало 60 человек. 21.11.13 было принято на работу еще 3 человека. Найти средний уровень ряда.
| Дата | Число человек
| Число дней,
| 
|
| 01.11.2013 | |||
| … | |||
| 09.11.2013 | |||
| 10.11.2013 | |||
| … | |||
| 20.11.2013 | |||
| 21.11.2013 | |||
| … | … | ||
| 30.11.2013 | |||
| Итого: |
Числовые характеристики ряда динамики.
Пусть имеется динамический ряд:
| t0 | Y0 |
| t1 | Y1 |
| …. | …. |
| tn | yn |
– базовый абсолютный прирост.
Он показывает,
– цепной абсолютный прирост.
Он показывает,
Взаимосвязь:
– базовый коэффициент роста.
Он показывает,
–цепной коэффициент роста
Взаимосвязь:
Он показывает,
– базовый темп роста.
Он показывает,
–цепной темп роста
Он показывает,
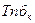
– базовый темп прироста
Он показывает,
= 
-- цепной темп прироста
Он показывает,
Пример: Имеются данные об объеме продукции (кг), производимой предприятием в течение 3 месяцев.
| Месяц | номер, k | yk | Абсолютный прирост | Коэффициент роста | Темп роста | Темпы прироста | ||||
| Δyбк | Δyцк | Крбк | Крцк | Трбк | Трцк | Тпбк | Тпцк | |||
| Январь | ||||||||||
| Февраль | ||||||||||
| Март | ||||||||||
Взаимосвязь цепных и базисных показателей
Пусть имеется динамический ряд:
| t0 | y0 |
| t1 | Y 1 |
| …. | …. |
| tn | yn |
Найдем сумму всех цепных абсолютных приростов:
Найдем произведение всех цепных коэффициентов роста:
Расчет средних числовых характеристик динамического ряда
Средний абсолютный прирост:
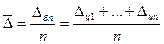
Или, поскольку 
, то 
В примере:
Средний коэффициент роста:
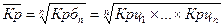
В примере:
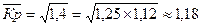
Динамическое прогнозирование
Процесс нахождения неизвестного уровня ряда, находящегося в данном динамическом ряду, называется интерполяцией.
Процесс нахождения неизвестного уровня ряда находящегося за пределами данного ряда называется экстраполяцией (прогноз на будущее).
По среднему абсолютному приросту. 
= 
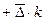
где
– число периодов, на который нужно «заглянуть» в будущее;
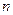- номер последнего_уровня исследуемого периода, за который рассчитан средний абсолютный прирост;
Пример: В 2006 году 1 кг помидоров в августе-месяце стоил 43 руб., а в августе 2014 года – 65 руб. Спрогнозировать уровень цен на помидоры в августе 2014 и 2016 гг.
Тогда средний абсолютный прирост равен
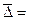
Получаем:
.
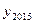
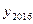По среднему коэффициенту роста
Прогнозирование по среднему темпу роста осуществляется в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции необходимо определить средний темп роста, возведенный в степень, соответствующую периоду экстраполяции, т. е. по формуле
= 
Имеются данные о темпах инфляции (в % к прошлому месяце) на основной набор продуктов питания:
| месяц | прирост цен на продукты питания (в % к прошлому месяцу) |
| янв | 1,5% |
| фев | 1,7% |
| мар | 0,8% |
| апр | 0,4% |
| май | 0,5% |
| июн | 0,8% |
| июл | 0,6% |
| авг | 0,8% |
| сен | 1,2% |
Вопросы:
§ Как изменились цены за рассматриваемый период?
§ Как изменялись цены в среднем ежемесячно?
§ Какую можно ожидать стоимость основного набора продуктов питания в октябре, ноябре и декабре текущего года, если в декабре предыдущего года он составлял 6 тыс. 200 руб.?
