Для расчета переходных процессо при пуске, линеаризуем механические характеристики привода. В результате получим прямые, изображенные на рисунке 2.1, по которым и будем вести счет.
Время работы на каждой j-ой ступени можно определить как:

Где - электромеханическая постоянная времени
- угловая скорость двигателя на j-ой ступени соответствующая статистическому моменту(рад/c)
Начальная и конечная угловые скорости двигателя на j-ой ступени (рад/c)
Электромехническая постоянная времени привода на j-ой ступени определяется из выражения:
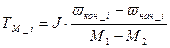
Где пиковый и переключающий момент (Н·м)
Временные зависимости и момента будем рассчиывать используя следующие выражения:

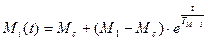
Используя рисунок 2.1 и формулы (5.4) и (5.3) для первой ступени получим:


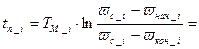

Подставляя выражения (5.5) и (5.6) значения выражения от нуля до рассчитываем зывисимости:




Данные расчета сводим в таблицу 5.1.
Таким же образом проводим расчет для других характеристик.
Для второй ступени








Данные расчета сводим в таблицу 5.2.
Для третьей ступени







Данные расчета сводим в таблицу 5.3.
Разгон по естествеенной характеристики. Так как разгона на естестееенной характеристики теоретически будет длиться бесконечно долго, то за конечную примем скорость, которая меньше на 3% от статической

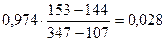

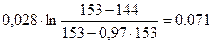




Данные расчета сводим в таблицу 5.4.
Таким образом, время пуска из неподвижного состояния до установившейся скорости составит

Таблица 5.1 Таблица 5.2
| t, c | ω, рад/c | n, об/мин | М, Н·м |
| 0,0346 | 8,8 | ||
| 0,0692 | 16,7 | ||
| 0,1038 | 23,9 | ||
| 0,1384 | 29,5 | ||
| 0,173 | 37,6 |
| t, c | ω, рад/c | n, об/мин | М, Н·м |
| 0 0,2472 0,4944 0,7416 0,9888 1,236 | 37,6 44,5 54 62 68 77 | 495 581 667 739 | 303 278 223 175 121 |
Таблица 5.3 Таблица 5.4
| t, c | ω, рад/c | n, об/мин | М, Н·м |
| 0,0452 | |||
| 0,0904 | |||
| 0,1356 | |||
| 0,1808 | |||
| 0,226 |
| t, c | ω, рад/c | n, об/мин | М, Н·м |
| 0 0,0142 0,0284 0,0426 0,0568 0,071 | 119 125 128 134 140 146 | 1086 1163 1245 1323 1389 1468 | 315 289 254 213 167 |
Для удобства построения графиков переходных процессов составим таблицу 5.5, в которой к взятым моментам времени прибавим время разгона на предыдущих ступенях. По результатам таблицы 5.5 строим времнные зависимости скорости и момента - рисунки 5.1 и 5.2 соответсвенно.
| t, c | ω, рад/c | n, об/мин | М, Н·м |
| 0,0525 | 7,8 | ||
| 0,0997 | 16,7 | ||
| 0,1185 | 23,9 | ||
| 0,268 | 29,5 | ||
| 0,357 | 37,6 | ||
| 0,460 | 44,5 | ||
| 0,534 | |||
| 0,612 | |||
| 0,710 | |||
| 0,810 | |||
| 0,957 | |||
| 1,034 | |||
| 1,122 | |||
| 1,200 | |||
| 1,289 | |||
| 1,345 | |||
| 1,432 | |||
| 1,523 | |||
| 1,612 | |||
| 1,7 |
Таблица 5.5 – переходные процессы при пуске.
Рисунок 5.1 – Кривая изменения скорости при пуске двигателя
Рисунок 5.2 – Кривая изменения скорости при пуске двигателя
5.2 Расчет переходных процессов при динамическом торможении
Для расчета переходных процессов при торможении будем использовать графоаналитическим методом. Для этого построим кривую динамического момента в тормозном режиме, пос следцющей формуле

Результаты расчета сводим в таблицу 5.6.
Динамический момент в тормозном режиме изображен на рисунке 5.3 кривая 1.
Таблица 5.6.
| s |  , рад/с , рад/с
|  , Н· м , Н· м
|  , Н· м , Н· м
|
| 1.00 0.95 0.90 0.85 0.80 0.75 0.70 0.65 0.60 0.55 0.50 | 157,08 149,226 141,372 133,14 125,66 117,8 109 102,1 94,24 86,4 78,54 | -370 -398 -412 -416 -415 -411 -405 -400 -395 -391 -386 | -40 -68 -82 -86 -85 -81 -75 -70 -65 -61 -56 |
| s |  , рад/с , рад/с
|  , Н· м , Н· м
|  , Н· м , Н· м
|
| 0.45 0.40 0.35 0.30 0.25 0.20 0.15 0.10 0.05 0 | 70.6 62,83 54.9 47,12 39,2 31,41 23.56 15,7 7,8 | -383 -379 -376 -374 -371 -369 -367 -365 -364 -330 | -53 -49 -46 -44 -41 -39 -37 -35 -34 |
Делим кривую динамического момента от скорости до нуля на участки с шагом. В результате получим тридцать олин участок, на каждом из которых момент предполагаем момент неизменным и равным среднему значению. Время торможения на каждом j-ом участке будет определяться по формуле:

Тогда полное время торможения определим как:

Результаты расчета сводим в таблицу 5.7.
Из последней строчки таблицы видно, что время торможения составляет 0,319
Таблица 5.6.
Переходные процессы при торможении
 , рад/с , рад/с
|  , рад/с , рад/с
| n, об/мин |  , Н· м , Н· м
|  , Н· м , Н· м
| Δt,с | t,с |
| -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 | 1490 1433 1375 1318 1230 1146 1089 1031 965 859 802 754 630 554 458 401 303 229 150 57 0 | -367 -396 -408 -406 -405 -401 -398 -394 -385 -384 -383 -380 -377 -375 -372 -369 -365 -363 -361 -360 -333 | -37 -66 -78 -76 -75 -71 -68 -64 -55 -54 -53 -50 -47 -44 -42 -39 -35 -33 -31 -30 | 0,021 0,021 0,020 0,020 0,020 0,020 0,020 0,020 0,020 0,020 0,019 0,019 0.019 0,019 0,019 0,018 0,018 0,018 0,018 0,017 0,017 | 0,021 0,042 0,062 0,082 0,102 0,122 0,142 0,162 0,182 0,202 0,219 0,239 0,258 0,278 0,299 0,318 0,339 0,359 0,379 0,397 0,415 |
По данным таблицы строим кривые изменения скорости и момента от времени - кривые 2 и 3 соответсвенно на рисунке 5.3.
1. Динамический момет торможения
2. Зависимость
3. Зависимость
Рисунок 5.3 – Кривые изменения скорости и момента в тормозном режиме
6. Проверка предварительного выбранного двигателя по нагреву и перегрузке
Проверка двигателя по нагреву произведем по рекомендациям, изложенным в [6], по методу эквивалентного момента. По этой методике эквивалентный момент за полный цикл работы не должен превышать номинального момента двигателя

Эквивалентный момент двигателя за полный цикл работы определяется как:

Где - рабочие моменты двигателя на первом,втором,третьем, n-ом участках времени (Н·м).
- длительность первого,второго,третьего, n-го участка (с).
Для определения рабочих моментов в момент пуска двигателя, разобьем кривую изменения момента на прямолинейные участки как это показано на рисунке 6.1
.
Рисунок 6.1 – Замена криволинейного графика нагрузки при пуске отрезками прямой
Тогда рабочий момент на пером участке определим как:

Аналогичным образом по формуле (6.3) находим рабочие моменты для других участков при пуске. Для торого и третьего участков:

Для четвертого учатка:

Для определения рабочих моментов приторможении двигателя, также разобьем кривую изменения момента на прямолинейные участки как это паказано на рисунке 6.2.
Рисунок 6.2. – Замена криволинейного графика нагрузки при торможении отрезками прямой.
По рисунку 6.2 определяем
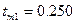 ,
,  ,
,  ,
, 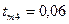
Тогда по формуле(6.3) находим рабочие моменты на участках торможения:




Для рассматриваемого цикла формула (6.2) примет вид:

Где и - коэффециенты, учитывающие ухудшение условий охлаждения соответственно при пуске, торможении и остановке.
Для закрытых самовентилируемых двигателей, каким и является рассматриваемый двигатель, коэффециент равен 0,5. Коэфециент рассчитываем по седующей формуле:

Подставляя числовые значения в формулу (6.2) мы получим следующее значение эквивалентного момента:


Полученный эквивалнтый момент не превышает номинального момента двигателя равного 112. Эквивалентный и номинальный момент двигателя незначительно отличаются от друг друга,следовательно, двигатель будет эффективно использован по нагреву.
Осущевствим проверку двигателя по допустимой перегрузке по методике исложенной [6]. Для асинхронных двигателей максимальный статистический момент на валу не должен превышать критического момента двигателя. Для заданной нагрузочной диаграммы максимальный момент на валу дигателя равен моменту. Тогда получим следующее неравенство:
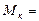 408 >
408 >  107
107
Оперделим перегрузочную способность λ при моменте:

Из последнего выражения видно, что двигатель имеет значительный запас по пкркгрузочной способности.
7 Расчет потерь энергии в двигателе и внешнем сопротивлении.
7.1 Расчет потерь энергии при пуске
Расчет потерь произведемпо методике изложенной [6]. Потери в роторной цепи при пуске под нагрузкой от начальной до скорости на каждой j-ой ступени определяются как:
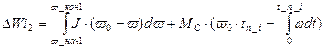 (7.1)
(7.1)
Зная, что при разгоне, скорость во времени изменяется по выражению (5.5) и интегрируя выражение (7.7) получим:
 (7.1`)
(7.1`)

Необходимые для расчета потерь энергии значения скорости, время пуска и постоянные времени были получены нами ранее пункте 5.1.
Потери в роторе и о нешнем резисторе распределяются пропорционально их сопротилениям:
 (7.2)
(7.2)
 (7.3)
(7.3)
Где:
- приведенное сопротивлние ротора
- приведенное сопротивление роторной цепи
- приведенное сопротивление внешнего резистора.
Потери в статоре определяются как:
 (7.4)
(7.4)
Где
- сопротивление статора
Подставляя числовые значения в формулы (7.1`), (7.2), (7.3), (7.4) для разгона на первой ступени получаем:








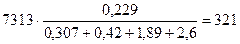
Суммарные потери при пуске на первой ступени:

Аналогичным образом рассчитываем потери для пуска на остальных ступенях
Для разгона второй ступени:








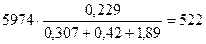

Для третьей ступени








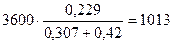

Для разгона по естественной характеристики 









Суммарные потери энергии при пуске: в статоре:

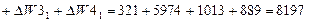
в роторе:


Во внешнем сопротивлении:


Полные потери в пуске


7.2 Расчет потерь энергии при торможении
Для определения потерь энергии роторной цепи при торможении под нагрузкой от скорости до (7.1) примет вид

Для нашего случая имеем:
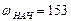


Так как аналитическая зависимость скорости от ремени при торможении неизвестна, то для нахождения интеграла вычислим площадь под кривой при торможении. Для этого заменим эту кривую прямой линией, как это показано на рисунке 7.1. Тогда по формуле (7.1) с учетом линеаризации получим.


Потери энергии в роторе и во внешнем резисторе находим по формулам (7.2) и (7.3) соответственно:

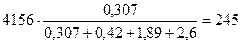
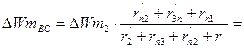

По формуле из (6) потери энергии в статоре при динамическом торможении определяются как:

По формуле (7.5) находим полные потери энергии при динаmмическом торможении

Максимальные потери в двигателе происходят при разгоне на второй ступени. При пуске на последующих ступенях потери уменьшаются. Это объясняется тем, что на второй ступени наибольшая разница между начальной и конечной скоростями и наибольшее время разгона. Потери в статоре на каждой из ступеней меньше, чем потери
а роторе. Потери энергии в роторе двигателя и во внешнем резисторе распределяются пропорционально их сопротивлениям. Потери в роторной цепи не зависят от ее сопротивления, в то время как потери в статоре обратно пропорциональны его величине.
Рисунок 7.1 - Замена криволинейного графика изменения скорости при торможении прямой линией.






