ПО МАТЕМАТИКЕ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОБУЧЕНИЯ
Направления подготовки
Электроэнергетика и электротехника
Правила выполнения и оформления контрольных работ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), названия дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в университет и адрес студента. В конце работы следует поставить дату её выполнения и подпись студента.
3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта не зачитываются.
4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи надо полностью вписать ее условие. В том случае, если несколько задач, на которых студент выбирает задачи своего варианта, имеют общую формулировку, следует переписывать условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7. После получения прорецензированной работы, как не зачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
Студент должен выполнять вариант, номер которого совпадает с цифрой его шифра (номера зачетной книжки), если последняя цифра 0, то решают задачи с 10, 20…
| № | Номера контрольных работ | ||||||||
| Вар | №II(1) №II(2) | ||||||||
Контрольная работа №II(1)
Функции многих переменных. Неопределенный интеграл.
Определенный интеграл, его приложения.
1. Дана функция  . Показать, что
. Показать, что  .
.
2. Дана функция 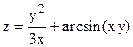 . Показать, что
. Показать, что  .
.
3. Дана функция z=ln(x2+y2+2x+1). Показать, что 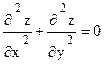 .
.
4. Дана функция  . Показать, что
. Показать, что  .
.
5. Дана функция 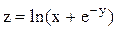 . Показать, что
. Показать, что  .
.
6. Дана функция  . Показать, что
. Показать, что  .
.
7. Дана функция z=  . Показать, что
. Показать, что  .
.
8. Дана функция 
 . Показать, что
. Показать, что  .
.
9. Дана функция z=sin(x+ay). Показать, что  .
.
10. Дана функция  . Показать, что
. Показать, что 
11-20. Даны функция z=(x; y), точка А(x0;y0) и вектор а. Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора а.
11. z = x2 + xy + y2; A(1; 1), a = 2 i - j.
12. z = 2x2 + 3 xy + y2; A(2; 1), a = 3 i - 4 j.
13. z = ln (x2 + 3y2); A(1; 1), a = 3 i + 2 j.
14. z = ln (5x2 + 4y2); A(1; 1 ), a = 2 i - j.
15. z = 5x2 + 6 xy; A(2; 1), a = i + 2 j.
16. z = arctg (xy2); A(2; 3), a = 4 i - 3 j.
17. z = arcsin  ; A(1; 2), a = 5 i - 12 j.
; A(1; 2), a = 5 i - 12 j.
18. z = ln (3x2 + 4y2); A(1; 3), a = 2 i - j.
19. z = 3x4 + 2x2y3; A(- 1; 2), a = 4 i - 3 j.
20. z = 3x2y2 + 5y2x; A(1; 1), a = 2 i + j.
21-30. Найти неопределенные интегралы. В первом примере результат проверить дифференцированием.
21. a)  ; б)
; б)  ;
;
22. a) 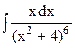 ; б)
; б)  ;
;
23. a)  ; б)
; б) 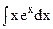 ;
;
24. a)  ; б)
; б)  ;
;
25. a)  ; б)
; б)  ;
;
26. а)  ; б)
; б) 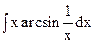 ;
;
27. a)  ; б)
; б)  ;
;
28. a)  ; б)
; б)  ;
;
29. a) 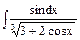 ; б)
; б)  ;
;
30. a)  ; б)
; б)  ;
;
31-40. Вычислить несобственный интеграл или доказать его расходимость.
31.  . 32.
. 32.  .
.
33. 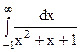 . 34.
. 34. 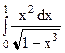 .
.
35.  . 36.
. 36.  .
.
37.  . 38.
. 38.  .
.
39.  . 40.
. 40.  .
.
Контрольная работа №II(2)






