Методические указания к решению задания 3

Для вариантов 1-10.

Процесс перехода насыщенного пара в перегретый осуществляется при постоянном давлении. Начальная точка процесса 1 образуется пересеченном изобары со значением Р на диаграмме в координатах h —s и линии постоянной степени сухости х. Проецируя полученную точку на ось ординат, находим значение энтальпии h₁ кДж/кг. Затем перемещаясь по изобаре, до пересечения с заданной температурой t₂, находим точку 2. Проецируя эту точку на ось ординат, находим энтальпию конечной точки процесса h₂.

Аналогично находим удельные объемы начального V₁ и конечного V₂ состояний, то есть проводим изохоры, проходящие через найденные точки (изохоры на h — s диаграмме изображаются пунктирными линиями). Их значения нанесены на диаграмму h —s в верхней части.

 

Количество подведенного тепла:

q=h2-h1 кДж/кг

Изменение внутренней энергии:

 

Δu=u2-u1=(h2–Pv2)–(h1–Pv1) кДж/кг

Для вариантов 11-20.

По заданым параметрам находим точку 1, то есть ищем точку пересечения изобары P₁ и степени сухости X. Проецируя ее на ось ординат, находим энтальпию h₁. По изохоре (штриховая линия), проходящей через начальную точку, находим V1 поднимаясь по ней до ее значения. Чтобы найти коночную точку 2, надо переместиться по изохоре значения V₁ до заданной конечной температуры t₂. Значения температуры нанесены на правой стороне диаграммы. Проецируя полученную точку на ось ординат, получим h₂. Значение Р₂ находим по пересекающей точку 2 изобаре.

Количество подведенного тепла для изохорного процесса:

 

q = Δu = (h2 – P2v2) – (h1-P1v1) кДж/кг

 

так как работа процесса ℓ=0

 

Для вариантов 21-30.

По начальным праметрам находим точку 1, полученную в результате пересечения изобары со значением Р₁ и изотермы со значением t₁. Проецируя ее на ось ординат, находим энтальпию h₁ Изохора, проходящая через найденную точку, соответствует объему V₁ так как изменение энтропии при адиабатном процессе равно нулю, то в h — s — диаграмме адиабата изображается вертикальной прямой. Поэтому из точки 1 проводим вертикальную линию до пересечения с изобарой Р₂. Проецируя точку 2 на ось ординат, получаем энтальпию h2. находим в этой точке степень сухости пара X₂, объем пара X₂, конечную t₂ Эта температура определяется изотермой, проходящей через точку пересечения изобары Р₂ с пограничной кривой X=1

Работа полученная в результате расширения ℓ=-Δu

Δu = (h1-P1v1) – (h2-P2v2)

 

Задание 4

Варианты 1-10

Для цикла поршневого двигателя внутреннего сгорания с подводом теплоты при υ — const определить параметры характерных для цикла точек, количества подведенной и отведенной теплоты, термический КПД цикла и его полезную работу (кДж).

Дано: Р₁; t₁; ε; λ; k=1,4.

Рабочее тело—воздух. Теплоемкость считать постоянной. Построить цикл в координатах

Р — υ.

Варианты 11-20

Необходимо найти давление и объем в характерных точках цикла двигателя внутреннего сгорания с подводом теплоты при Р - const, а также его термический КПД η₁ и полезную работу (кДж). Построить цикл в координатах Р — υ.

Дано: Р₁; ε; g; к = 1,4. Диаметр цилиндра d, м. ход поршня S. м. Рабочее тело — воздух. Теплоемкость считать постоянной.

данные	Варианты
P1, МПа	0,1	0,15	0,2	0,25	0,3	0,35	0,4	0,45	0,5	0,5	0,11	0,15	0,2	0,25	0,3
t1, oC
P3, МПа
ε
λ	1,6	1,2	1,25	1,5	2,0	2,5	3,0	3,5	3,2	2,6
р											1,2	1,3	1,4	1,5	1,6
d, M											0,3	0,2	0,15	0,15	0,13
S, M											0,25	0,2	0,2	0,18	0,15

Варианты 21-30

В цикле поршневого двигателя внутреннего сгорания со смешанным подводом теплоты начальное давление Р₁ МПа, начальная температура t₁ ^оС, количество подведенной теплоты

Q=1090 кДж. Степень сжатия ε.

Какая часть теплоты должна выделяться в процессе при υ— const, если максимальное давление составляет Р₃=Р₄ (МПа). Рабочее тело —воздух. Теплоемкость считать постоянной.

Данные	Вариант
P1, МПа	0,35	0,4	0,45	0,5	0,2	0,09	0,08	0,1	0,15	0,2	0,25	0,3	0,25	0,15	0,09
t1, oC
P3, МПа						4,4	4,5	4,6	4,8	4,0	4,2	3,8	3,6	4,3	4,5
ε
λ
р	1,7	1,8	1,9	2,0	1,8
d, M	0,15	0,16	0,16	0,16	0,18
S, M	0,15	0,2	0,2	0,2	0,2

 

Методические указания к решению задания 4

В решении задач вариантов 1-10 рассматривается цикл OТТО —цикл ДВС с подводом теплоты при постоянном объеме. Он состоит из 2-х

адиабат и 2-х изохор.

 

Характеристиками цикла являются:

 

ε = υ1/ υ2 — степень сжатия,

 

λ =P3/P2 — степень повышения давления;

 

количество подведенной теплоты

 

q1 = Cυ(T3-T2). (кДж/кг);

 

количество отведенной теплоты

q2= C1 (T4-T1) (кДж/кг)

работа цикла:

ℓ= q1 — q2 (кДж/кг)

 

 

термический КПД цикла:

 

η1 = 1-
ελ- 1

 

 

зависимость теплоемкости от t⁰ — const

 

В решении задач вариантов 11-20 рассчитывается цикл с подводом теплоты при постоянном давлении - цикл Дизеля. Он состоит из двух адиабат, одной изобары, одной изохоры.

 

Характеристиками цикла являются:

ε=υ1/υ2 —степень сжатия

ρ = υ₁/υ₂ — степень предварительного

расширения;

количество подведенной теплоты в цикле:

q2=Сp(T3-T2), (кДж/кг);

количество отведенной теплоты:

q = Сυ(Т4-Т1),(кДж/кг);

работа цикла:

L = q1-q2 (кДж/кг);

η1 = 1 -		.	ρk - 1
εk∙1	k (ρ – 1)

 

термический КПД цикла:

 

В результате решения строится диаграмма в координатах P — υ. Масшта б выбирается произвольно.

В решении задач вариантов 21-30 рассчитывается смешанный цикл - цикл Тринклера, который состоит из двух адиабат, двух изохор и одной изобары.

 

Характеристики цикла:

 

ε = υ1/υ2; λ = P3/P2; ρ = υ4/υ3

 

 

количество подведенной теплоты:

q₁ =С_υ(Т₃ — Т₂) + С_р(Т₄ — T₃),(кДж/кг);

количество отведенной теплоты:

q₂ = C_υ (T₄ – T₁(кДж/кг);

 

υ4

 

 

η1 = 1-		·	λρk - 1
εk – 1	λ – 1 + k· λ(ρ – 1)

термический КПД цикла:

 

 

Зависимость теплоемкости oт температуры принять постоянной.

В результате решения строится диаграмма в координатах Р — υ. Масштаб выбирается произвольно

 

Задание 5

Варианты 1-10

Определите количество тепла, передаваемого от дымовых газов к
кипящей воде через:

 

 

 

а) стальную чистую стенк толщиной δ₁;

б) стальную стенку, покрытую со стороны воды слоем накипи

толщиной δ₂. Температура дымовых газов t_г, температура кипящей воды t_в, коэффициент

теплоотдачи от газов к стенке

и от стенки к воде

 

в) стальную стенку, покрытую со стороны воды слоем накипи и слоем

 

масла толщиной δ₃

 

Данные	Задачи
δ1,мм							8,5	6,5	4,5	3,5
δ2,мм									8,5	7,5
tr, 0C
tв,0C
δз, мм		1,5	0,5	1,5	1,2	2,0	1,8	1,6	1,0	0,8

Варианты 11-20

Изолированная теплофикационная труба длиной L с наружным диаметром изоляции d проложена внутри прямоугольного бетонного канала, размером (а х b). Температуры, поверхностей изоляции трубы и стенок канала соответственно t₁ и t₂ а степени черноты соответственно равны ε₁ =0.9. ε₂ =0,7

 

Данные	Задачи
ι, м
d, мм
а, мм
b, мм
t1,0C
t2,0C

Определите для трубы потерю теплового потока.

 

Варианты 21-30

Необходимо нагреть за час массу m кг воды от температуры t'_в до t"_в дымовыми газами с начальной температурой t'_г. Расход дымовых газов m_г теплоемкость газов

 

Cрм=1,047	кДж
кг∙0С

 

теплопередачи коэффициент

 

к=163,3	Вт
м2∙0С

 

Определите поверхность нагрева F для прямотока.

 

Данные	Задачи
mв, кг
t'в, 0 C
t"в, 0 C
t'r, 0 C
mr, кг/ч

 

Методические указания к решению задания 5

Для вариантов 1-10

Для определения количества тепла, передаваемого дымовыми газами через однослойную стенку, используется формула:

 

 

q=к(tr-tв),	Вт
м2

где k —коэффициент теплопередачи, определяемый для случая а):

 

к=		∙	Вт
1/α1+δ/λ+1/α2	м2∙0С

Вт

м2∙0С

где δ — толщина стенки, м;

λ — коэффициент теплопроводности стенки,

 

 

α₁ и α₂ - коэффициенты теплоотдачи от газов к стенке и от стенки к воде

 

Для случаев б) и в);

 

k =
n 1/α1 + Σ ∙ δi/ λi+1/α2

 

где δ₁ — толщина каждого из слоев между газами и водой, м;

λ₁ - коэффициенты теплопроводности каждого из материалов,

Вт

м∙0С

составляющих слои стенки.

 

Для вариантов 11-20

 

где Cпр — приведенный коэффициент лучеи

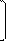Q = CnpF1.		Т1	4 -	T2

 

где C_пр – приведенный коэффициент лучеиспускания, определяемый как:

 

Спр = -	1
1/С1+F1/F2(1/C2 – 1/C0)

 

где С₁=С₀. ε и С₂=С₀. ε₂ — коэффициенты поверхностей Вт/м^{2 0}К⁴.

С =5,67 Вт/м^{2 0}К4 — постоянная излучения абсолютно черного тела;

ε₁ и ε₂ — степени черноты поверхностей;

F₁ — площадь внешней поверхности трубы, м²;

F₂ - площадь внутренней поверхности бетонного канала, м².

 

Для вариантов 21-30

Для определения поверхности нагрева используется уравнение:

Q = k · FΔcp. Вт,

 

где Q - тепловой поток, Вт;

Вт

м2∙0С

 

k — коэффициент теплопередачи,

 

F — поверхность нагрева, м²;

Δt_cр — средний температурный напор вдоль поверхности нагрева. Тепло, передаваемое воде, равно:

Q=mв Сpm(t'в-t"в).

 

где m_в — масса нагреваемой воды, кг;

С_pm — средняя изобарная теплоемкость воды, кДж/кг °С; (С_pm принять равной 4,19 кДж/кг°С)

t'в — начальная температура воды, °С;

t"в — конечная температура воды, °С.

Конечную температуру газов t"г определяем из уравнения теплового баланса:

.

Q = mг·Сpm2(t'г-t"г)

 

Далее необходимо рассчитать поверхность нагрева для прямотока:

 

F = Q/(Q∙ ∆tср),м2

 

 

∆tср=	∆tб-∆tм	если ∆tб/∆tм>1,7
ln∆tб/∆tм

 

где

 

где Δб = t'_г-t'_в;Δtм=t"_г-t"_в — максимальная и минимальная разности температур теплоносителей

Литература: 1, стр. 138…191; 3, стр. 62…93; 4, стр. 145…182; 5, стр. 203…277, 319…325

Задание 6

Определите низшую теплоту сгорания и объем воздуха, поступающего в топку для сжигания угля данного состава по рабочей массе. Коэффициент избытка воздуха α, температура воздуха t ^oС, часовой расход воздуха В. кг/ч.

 

Для определения потери теплового потока нужно воспользоваться формулой:

Данные	Задачи
CP, %	70,4	41,4									32,8
HP, %	5,02	2,9	6,22	3,1	2,88	4,2	4,6	5,2	2,8	6,0	2,4	3,5	4,2	4,0	5,1
OP, %	11,7	10,5	11,0	9,2	9,0	9,5	9,8	12,5	10,0	8,4	9,9	10,2	8,0	6,8	10,4
NP, %	0,88	1,0	1,9	0,7	0,5	0,9	1,5	1,6	1,8	2,0	0,6	2,1	3,2	2,2	0,6
SPл, %	2,0	0,9	2,2	2,0	1,9	0,9	0,8	1,5	1,8	1,6	2,9	0,9	2,2	15,8	12,9
AP, %	5,0	24,3	6,0	8,3	12,0	10,8	5,8	11,6	16,2	15,1	18,4	7,5	5,0	6,2	8,2
WP, %	5,0	19,0	4,68	24,7	23,72	9,7	17,5	9,6	17,4	24,9	33,0	37,8	37,4		16,8
α	1,5	1,35	1,4	1,7	1,3	1,2	1,6	1,65	1,4	1,3	1,4	1,2	1,4	1,4	1,3
t1, 0C
B, кг/ч

 

Продолжение

 

Данные	Задачи
CP, %	48,4	52,3	54,8	56,0	62,8	65,5		74,2		71,5	70,0	50,6		70,7
HP, %	5,2	6,4	2,5	5,0	4,2	5,6	5,4	5,3	5,2	5,2	5,3		7,2	6,2	5,6
OP, %	11,9	9,5	10,0	12,5	9,6	2,4	1,5	1,8	14,4	10,2	9,6	12,2	10,2	8,5	12,0
NP, %	1,5	0,5	1,2	1,6	0,9	5,6	3,8	1,2	1,3	1,7	1,5	2,5	0,3	0,9	2,3
SPл, %	2,2	2,0	2,5	1,5	0,8	0,7	4,5	2,0	6,1	2,7	0,8	0,3	4,9	2,2	1,9
AP, %	21,0	15,2	16,0	17,0	10,8	8,5	4,0	4,5	5,0	5,2	4,2	12,4	6,3	5,0	4,2
WP, %	9,8	14,1		6,4	10,9	11,7	9,8		7,0	3,5	8,6		17,1	6,5	9,0
α	1,3	1,35	1,35	1,2	1,2	1,25	1,6	1,5	1,55	1,7	1,65	1,2	1,3	1,4	1,5
t1, 0C
B, кг/ч

 

 

Методические указания к решению задания 6

 

Для нахождения низшей теплоты сгорания необходимо воспользоваться формулой Д. И. Менделеева:

Q^p_H = 338C^P + 1025H^P -108.5(O^P-S^p_л)- 25W^p, кДж/кг, где С^р. Н^р. О^р, S^p, W^p — составляющие рабочей массы топлива в %.

Теоретическое количество воздуха определяется:

V_o = 0,0899К^р + 0,266Н^р - 0,ЗЗЗО^р, м³/кг, где K^p = C^p + O,375S^p_л.

Действительное количество воздуха V = αV_o, м³/кг.

Далее можно найти часовой расход воздуха: V_в = V ∙ В, м³/ч.

Учитывая температуру воздуха:

V’в= Vв∙ 1+	t	м3/ч

Литература:1,стр. 195…207; 3, стр. 93…103; 4,стр. 183…212