Пусть φ ′(x) ≠ 0 в окрестности точки x0
Если существует предел
, то 
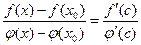, где с лежит между x0 и х.
При x→x0 величина с также стремится к х0; перейдем в предыдущем равенстве к пределу:
Так как , то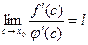 
.
Поэтому 
(предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует)
47.
Правило Лопиталя, при ∞ / ∞.
Пусть функции f(x) и φ(x) непрерывны и дифференцируемы в окрестности точки x0 (кроме точки x0), в этой окрестности
Если существует предел
, то
Неопределенности вида 0∙∞; ∞-∞; 1∞; ∞0; 00 сводятся к двум основным.
Например, 0∙∞
Пусть f(x)→0, φ(x)→∞ при х→х0
48. Если для х2>x1,где (х2,x1)€[a, b] выполняется условие f(х2)>f(x1), то y=f(x) наз. возрастающей на [a, b]. Если для х2>x1,где (х2,x1)€[a, b] выполняется условие f(х2)<f(x1), то y=f(x) наз. убывающей. Необходимое условие: если дифференциал на интервале (a, b), f(x) убывает, то f’(x)≤0 для любых х€(a, b). Достаточное условие: Если f(x) диффер. на (a, b) и f’(x)<0 (f’(x)>0) для любых х€(a, b), то f(x)возрастает(убывает) на интервале (a, b).
49. точка х0 наз. точкой максимума функции y=f(x), если сущ. такая σ-окрестность точки х0, что для всех х≠ х0 из этой окрестности выполняется неравенство f(х2)<f(x0). Аналогично определяется точка минимума функции.
50.
51. всякая непрерывная на отрезке ab функция достигает своего наибольшего (M) и наименьшего (m) значения. Если наибольшее или наименьшее значение достигается во внутренних точках, то эти точки могут быть только точками экстремума.
Правило:1.Найти все критические точки функции на интервале ab. 2. Вычислить начение точки в критических точках. 3. Выислить зачение функции на концах отрезка. 4. Из всех полученных значений выбрать (M) и (m).
52. Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках.
Линия наз-ся вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.
Необходимый признак выпуклости и вогнутости: если линия на интервале выпуклая, то ее 2я производная <=0; если линия на интервале вогнутая, то ее f``(x)>=0
Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; если f``(x)>0, то линия вогнутая
53. Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.
Признаки точки перегиба: чтобы X0 была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через х0.
54. Асимптота - прямая, к которой график ф-ции стремится, но никогда ее не пересекает.
1) прямая х=х0 назыв-ся вертикальной асимптотой графика ф-ции f(x)=y, если при х®х0 |f(x)|®+¥ (вида x=b)
2) y=kx+b,,y=f(x) - общее ур-е наклонной асимптоты
lim[f(x)-(kx+b)]=0, f(x)=kx+b+a(б.м.в.) по св-ву x®¥ пределов.
разделим левую и правую части на х. Возьмем предел при х®¥
f(x)/x=k+b/x+a/x, lim(f(x)/x)=limk+lim(b/x)+lim(a/x)
x®¥, то
k=lim(f(x)/x)
b=lim[f(x)-kx]
Если эти пределы существуют, то существует и наклонная асимптота вида kx+b=y
3)k=lim(f(x)/x)=0, y=b - горизонтальная асимптота.
55. -обл. определения ф-ции
-точки разрыва и интервалы, где ф-ция явл-ся непрерывной
-поведение ф-ции в окрестностях точки разрыва, вертикальной асимптоты
-т. пересечения графика с осями координат
-симметрия графика (чет./нечет):
f(-x)=x симметрична относительно осей
f(-x)=-x симметрична относительно О(0,0)
-периодичность
-интервалы монотонности
-точки экстремума
-наибольшее и наименьшее значение
-выпуклость, вогнутость
-точки перегиба
-поведение ф-ции в безконечности, наклонная и горизонтальные асимптоты
-нанесение на график.
