Очень многие реальные системы имеют сложную структуру, которая может и не сводиться к последовательным или параллельным соединениям элементов. Наиболее простой пример подобных структур показан на рис 6.1 – это так называемая мостовая схема [6].
|
Большинство таких практических систем характеризуются рядом свойств, заключающихся в том, что их характеристики надежности монотонно ухудшаются при ухудшении характеристик надежности составляющих их элементов.
Методов оценки таких систем много. Рассмотрим основные из них.
Метод прямого перебора
Произвольная система, состоящая из “n”-элементов, каждый из которых может находиться в состоянии работоспособности (1) и в состоянии отказа (0), может находиться в “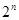 
” различных состояниях;
– все n элементов работоспособны,
– отказал i-й элемент, остальные – работоспособны.
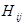– отказали i-й и j-й элементы, остальные – работоспособны.
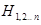– отказали все элементы.
Если определен критерий отказа, то всё множество состояний системы можно разделить на два подмножества: подмножество состояний работоспособности F и подмножество состояний отказа G. Тогда, если для каждого состояния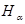 
вычислить вероятность появления 
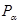, то вероятность состояния работоспособности системы:
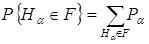(3.29)
где знак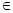 
означает суммирование по всем состояниям, относящимся к подмножеству F.
Если система состоит из взаимно независимых элементов, то вероятность соответствующих состояний вычисляется по формулам:
; 
; 
.
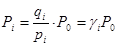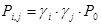(3.30)
где 
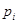и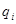 
– вероятности состояния работоспособности и неработоспособности,
Рассчитаем, к примеру, надежность мостиковой схемы, состоящей из пяти идентичных элементов с 
. Для определения вероятности безотказной работы, к примеру, за 10 часов работы и среднего времени работы до отказа схемы составляем таблицу возможных состояний (табл. 3.1) и по схеме рис. 3.7 непосредственно определяем к какому из подмножеств F или G относится то или иное состояние.
Таблица 3.1 Возможные состояния мостиковой схемы.
| Индекс состояния α | Состояние элемента | Вид подмножества | Вероятность состояния Рα | ||||
| 1,2 1,3 1,4 1,5 2,3 2,4 2,5 3,4 3,5 4,5 1,3,4 1,3,5 1,4,5 2,3,4 2,3,5 2,4,5 3,4,5 1,3,4,5 | F F F F F F G F F F F F F F F G F G G G F G G G |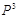 
|
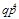
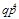
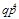
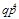
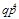
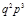
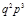
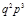
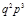
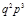
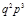
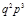
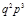
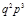
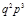
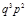
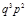
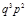
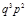
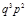
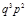
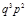
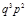
Таким образом согласно (3.29)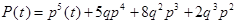 
(3.31)
Заменив p на «1-q», получим:
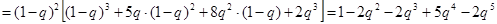(3.32)
Т.к. обычно «q» мало, то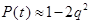 
; (3.33)
Или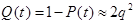 
; (3.34)
В нашем случае вероятность безотказной работы элемента:
, а 
.
Тогда вероятность безотказной работы мостиковой системы:
.
Для вычисления средней наработки до отказа удобнее представить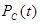 
, как функцию от вероятности безотказной работы элементов, для чего, заменив в (3.31) q на ”1-p”, получим:
(3.35)
По общей формуле 
, и, учитывая, что для нашего случая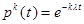 
, получаем, интегрируя:
Как видно из приведенного метод точен, но громоздок.
Другие, ниже приведенные методы позволяют прийти к финишу более кротким и быстрым путем.
