Комбинационное рассеяние света

ДИСПЕРСИЯ СВЕТА

 

Строгий подход к вопросу о механизме взаимодействия электромагнитного излучения с веществом, требует привлечения представлений и математического аппарата квантовой механики. Однако, как показал Лоренц, основные выводы относительно большинства оптических явлений можно получить, если рассматривать вещество как систему заряженных частиц, образованную ядрами атомов и квазиупруго связанными с ними электронами. Если один из таких электронов вывести из положения равновесия, то он будет совершать гармонические колебания с собственной частотой ω₀, значение которой зависит от строения атома и места электрона в нем. Колеблющийся электрон и ядро атома образуют электрический диполь с переменным моментом р_е = e·r, где е – заряд электрона, r – плечо зарядового диполя (расстояние от электрона до ядра). В соответствии с постулатами Максвелла это означает, что такая система будет излучать электромагнитную волну. В системе электрон–ядро колебания будет совершать и электрон, и ядро. Однако амплитуда колебаний ядра столь незначительна, что колебаниями ядра можно пренебречь. Т.к. на генерирование волны требуется энергия, то колебания будут затухающими.

Рассмотрим, что произойдет, если электромагнитная волна, т.е. переменное электромагнитное поле, частотой ω проникнет в вещество. Со стороны этого поля на все электроны атомов и молекул будет действовать переменная электрическая сила:

F _i = еЕ _i = eE₀ cos(ωt + φ_{0, i} ), (1)

где е – заряд электрона, Е _i = E₀ cos(ωt + φ_{0, i}) – напряженность поля в точке, где расположен i –ый электрон, φ_{0, i} – начальная фаза, которая определяется положением электрона в атоме. Под воздействием этой силы электроны будут совершать вынужденные колебания с частотой ω, уравнение которых можно найти, решив дифференциальное уравнение вида (см. Лк № 2):

, (2)

 

где s – смещение электрона от положения равновесия, ω_{0, i} – собствен-

ная частота электронов i –ого сорта, β – коэффициент затухания, m_e – масса электрона. Это уравнение мы записали по аналогии с дифференциальным уравнением механических вынужденных колебаний. Решение (2) имеет вид:

s = Аcos(ωt – φ), (3)

где амплитуда

, (4)

а отставание по фазе колебаний электрона от изменений переменной силы (1) будет определяться выражением:

, (5)

Вынужденные колебания электрона обуславливают излучение системой электрон-ядро вторичных электромагнитных волн, которые будут распространяться в среде со скоростью υ. Если среда оптически однородна, то вторичные волны будут когерентны как между собой, так и с падающей волной. Интерферируя друг с другом и с первичной волной, вторичные волны образуют в направлении падающей результирующую волну, которая имеет ту же частоту, что и падающее излучение, но отличается от него амплитудой и фазой. Это означает, что скорость υ распространения результирующей волны в среде не будет равна скорости света в вакууме.

Как известно, отличие скорости света υ в данной среде от скорости света в вакууме характеризуется абсолютным показателем преломления n. Увяжем значение n с параметрами вынужденных колебаний электронов. Т.к. n = с/υ = , а магнитная проницаемость μ для диэлектриков равна единице, то

n = . (6)

Диэлектрическую проницаемость ε среды можно выразить через модуль вектора поляризации , где р_{е, i} индуцированный дипольный момент электрона, V – объём вещества.

, (7)

где χ – диэлектрическая восприимчивость среды, ε₀ – диэлектрическая постоянная.

Модуль индуцированного дипольного момента электрона, совершающего вынужденные колебания р_е = е·s(t), где s(t) – мгновенное значение смещения. Если пренебречь затуханием (β = 0), то с учётом (3) и (4) получим:

. (8)

Молекула в целом приобретает электрический дипольный момент

. (9)

Суммирование ведется по всем k электронам молекулы. Умножив р_м(t) на число молекул в единице объема N, получим мгновенное значение вектора поляризации вещества:

Р(t) = N· p_м = N . (10)

Подставляя в (7) Р/Е(t) из (10), получим в соответствии с (6) для n² = ε:

. (11)

Как видно из (11), скорость электромагнитного излучения в данной среде тем больше отличается от её значения для вакуума, чем ближе частота вынужденных колебаний ω к собственной частоте электронов i –ого сорта – ω_{0, i}.

Таким образом, значение скорости результирующей волны в среде зависит не только от природы вещества, но и от частоты падающего излучения. В оптическом диапазоне это явление получило название дисперсии света.

В частности дисперсией объясняется разложение белого света (λ = 400÷700 нм) при преломлении на границе раздела двух сред на простые монохроматические волны. При этом образуется окрашенная полоска с непрерывным переходом цветов от красного к фиолетовому, которую Ньютон назвал спектром (spectrum – видение, лат.).

Явление дисперсии обычно определяют как зависимость показателя преломления n от длины волны – n = f(λ) или от частоты – n = f(ω).

График зависимости n = f(ω) в соответствии с (11) для двух резонансных частот будет иметь вид, представленный на рис.1. Как видно из графика, при приближении значения ω к одной из собственных частот колебаний электронов ω_{0, i} n² неограниченно растёт (пунктирная линия, рис.1). Такое поведение функции в области собственных частот электронов обусловлено пренебрежением затухания. Реальный ход графика в области собственных частот электронов, т.е. с учётом зату- затухания, показан сплошной линией.

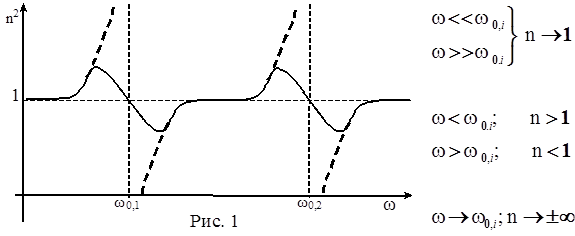
Быстроту изменения показателя преломления характеризуют величиной , которая называется дисперсией вещества.

Перейдём к зависимости n = f(λ) (рис.2, сплошная линия) и проанализируем поведение дисперсии вещества как функции длины волны. На участках 1 – 2 и 3 – 4 D < 0, т.е. с ростом λ показатель преломления n убывает, причем по мере приближения к значениям резонансных длин волн скорость изменения n растет. Эта область нормальной дисперсии.

На участке 2 – 3 D > 0 и показатель преломления увеличивается практически по линейному закону – область аномальной дисперсии. Это область совпадает с резонансной частотой колебаний электронов, что приводит к сильному поглощению энергии падающей электромагнитной волны.

Явление дисперсии лежит в основе широко известного метода качественного и количественного исследования веществ, который называется спектральным анализом. Практическое значение для этого метода имеет область нормальной дисперсии. Зависимость n = f(λ) в этом случае достаточно хорошо описывается функцией:

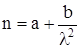, (12)

где а и b – const, зависящие от природы вещества (рис.3).

 

2. ПОГЛОЩЕНИЕ СВЕТА

Как уже было сказано, при прохождении пучка света через вещество его энергия растрачивается на возбуждение и поддержание колебаний электронов в атомах и молекулах. Частично эта энергия возвращается излучению в виде вторичных волн, а частично переходит в другие виды энергии, свойственные процессам, которые сопровождают колебательное движение электронов. Это рост теплового движения частиц, ионизация и возбуждение атомов, фотохимические реакции и т.д. Т.о. интенсивность пучка света после прохождения через вещество уменьшается за счёт превращения энергии электромагнитного поля в другие виды энергии – это явление называется поглощением света.

Рассмотрим, как изменяется интенсивность пучка света по мере его продвижения в веществе. Пусть на вещество падает пучок света интенсивностью I_0. Выделим на некоторой глубине элементарный слой толщиной d l, интенсивность на входе в который I _l (рис.4). Как установил Бугер, изменение интенсивности в этом слое:

dI _l = - μ I _l d l, (13)

где коэффициент пропорциональности μ зависит от свойств вещества и длины волны. Он называется монохроматическим натуральным показателем поглощения. [μ] = 1/м. Знак (-) в (13) указывает на убыль интенсивности света по мере продвижения пучка в веществе. Выражение (13) представляет собой дифференциальное уравнение первого порядка с разделяющимися переменными. Решим его:

; ; ; .

По определению логарифма окончательно имеем:

– закон Бугера -Ламберта. (14)

В целом поглощение света носит селективный характер, т.е. разные длины волн поглощаются по-разному: одни больше, другие меньше. В частности, этим фактом объясняется окраска прозрачных тел. Например, если данное вещество сильно поглощает коротковолновую часть спектра и слабо – длинноволновое излучение, то материал будет казаться красным. Особенно сильное поглощение наблюдается в области аномальной дисперсии – так называемое резонансное поглощение. На рис.2 пунктирной линией представлен график зависимости коэффициента поглощения μ от длины волны. Как видно из хода графика, максимум поглощения испытывают электромагнитные волны, частоты которых равны собственным частотам колебаний электронов в атомах вещества.

Этот факт имеет важное практическое значение, т.к. позволяет определить частоты собственных колебаний электронов в атомах и молекулах, тем самым даёт возможность судить о их структуре.

Для разреженных газов и паров в атомарном состоянии показатель поглощения для большинства длин волн близок к нулю и лишь для очень узких спектральных областей (Δλ ~10^-3 – 10^-4 нм) обнаруживает резкие максимумы (рис.5). Эти максимумы соответствуют резонансным частотам колебаний (длинам волн) электронов в практически не взаимодействующих друг с другом атомах – линейчатый спектр поглощения.

В случае многоатомных молекул обнаруживаются также частоты, соответствующие колебаниям атомов внутри молекулы. В результате спектры таких веществ представляют собой сравнительно широкие (~ 0,1–100 нм) полосы поглощения (рис.6). Это имеет место для твердых тел, а так же для жидкостей и газов под высоким давлением.

Для диэлектриков коэффициент поглощения невелик (10^-5 – 10^-7 м^-1), и хотя для них характерно селективное поглощение (μ велико только для определённых длин волн), в спектре наблюдаются довольно широкие полосы, что связано со строением диэлектриков.

Металлы практически непрозрачны для света (μ = 10⁵ – 10⁷ м^-1). Под воздействием электрического поля световой волны в них возникают быстропеременные токи, сопровождающиеся выделением джоулева тепла. Это приводит к быстрому превращению энергии волны во внутреннюю энергию металла. Чем выше концентрация свободных электронов в металле, тем сильнее в нем поглощается свет.

Исследуя поглощение света растворами окрашенных веществ, А. Бер показал, что в случае не поглощающего растворителя и малой концентрации растворенного вещества для монохроматического излучения коэффициент поглощения μ прямо пропорционален концентрации с:

μ = χ· с, (15)

где χ – показатель поглощения для раствора единичной концентрации. Если в соотношении (15) использовать молярную концентрацию с _μ, то χ называется натуральным молярным показателем поглощения.

Теперь закон Бугера -Ламберта для растворов примет вид:

. (16)

Это закон Бугера-Ламберта-Бера.

В лабораторной практике закон Бугера-Ламберта-Бера часто выражают через показательную функцию с основанием 10:

, (17)

где ε – молярный показатель поглощения ε = 0,43 χ.

Способность растворов поглощать свет характеризуют также коэффициентом светопропускания (прозрачностью) –

τ = I / I₀ (18)

и оптической плотностью раствора

 

D = lg(I₀ / I) = lg(1/τ) = εc l. (19)

 

На явлении поглощения основан ряд методов изучения физико-химических свойств материалов: абсорбционный спектральный анализ, спектрофотометрия и колориметрия. Эти методы используются при исследовании химического состава и структуры молекул вещества, характера движения электронов в металлах, зонной структуры полупроводников, определении концентрации растворов и т.д. При этом измеряемыми величинами являются: I, D и τ.

РАССЕЯНИЕ СВЕТА

При прохождении света через неоднородную среду ослабление интенсивности в направлении первичной волны происходит не только из-за поглощения, но и за счёт перераспределения части энергии на неоднородностях по другим направлениям. Это явление называется рассеянием света.

В однородной чистой среде, как известно, вторичные волны, возбуждённые падающим излучением, являются когерентными. В результате их интерференции происходит полное погасание волновых процессов во всех направлениях, кроме направления распространения первичной волны, т.е. рассеяние света отсутствует.

Картина меняется, если в среде имеются хаотически распределённые неоднородности соизмеримые с длиной волны. Дифракция световых волн на таких неоднородностях частично нарушает строгие фазовые соотношения вторичных волн, что приводит к достаточно равномерному распределению части интенсивности по всем направлениям.

Если неоднородность среды создаётся беспорядочно расположенными посторонними частицами, то говорят о рассеянии Тиндаля (или диффузном рассеянии). Такие среды называются мутными. К ним относятся дымы, туманы, суспензии, эмульсии и некоторые твёрдые тела (перламутр, опалы, молочные стёкла).

Рассеяние света наблюдается и в оптически чистых средах. Появление неоднородностей в этом случае обусловлено флуктуациями плотности вещества – ρ, возникающими в процессе хаотического теплового движения молекул. Этот тип рассеяния называется молекулярным рассеянием.

Изучение явления рассеяния показало, что интенсивность пучка в выбранном направлении тем больше, чем меньше размер неоднородностей по сравнению с длиной волны. При этом короткие волны испытывают более сильное рассеяние, чем длинные.

Рэлей установил, что для неоднородностей размером d < 0,2·λ

I ~ ~ ν⁴. (20)

Такая зависимость интенсивности рассеянного излучения от длины волны объясняет, почему небо имеет голубой цвет днём, а на закате кажется красным. Днём в глаз человека попадает рассеянный свет, в котором преимущественно содержится коротковолновое излучение. Утром или на закате мы воспринимаем прямые лучи, идущие от солнца и состоящие в основном из длинноволнового излучения.

Совокупность методов изучения явлений природы, основанных на измерении параметров рассеянного излучения, называется нефелометрией, а соответствующие приборы – нефелометрами.

Отметим в заключение, что в общем случае при взаимодействии пучка света с веществом имеют место оба явления. Учёт убыли энергии в направлении падающей волны из-за рассеяния видоизменит закон Бугера-Ламберта:

, (21)

 

где δ – показатель ослабления пучка света из-за рассеяния.

 

 

КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА

 

Комбинационное рассеяние было открыто в 1928 году (Раман, Кришнан, Ландсберг Г.С., Мандельштам Л.И.). Это явление заключается в том, что в спектре рассеяния газов, жидкостей и твёрдых тел наряду с длиной волны падающего излучения появляются частоты, представляющие собой комбинацию частоты падающего излучения ω₀ и частот ω _i колебательных или вращательных энергетических переходов рассеивающих молекул: ω= ω₀ ± ω _i.

Дополнительные линии в спектре комбинационного рассеяния выступают парами: «красные» спутники, т.е. линии смещённые в сторону меньших частот (больших длин волн) – ω_к = ω₀ - ω _i и «фиолетовые» спутники – ω_Ф = ω₀ + ω _i, смещённые в сторону коротковолнового излучения

Согласно квантовой теории процесс комбинационного рассеяния, можно интерпретировать как результат неупругого соударения фотонов с молекулами. При этом фотон может отдать молекуле или получить от неё некоторое количество энергии, равное разности энергий двух уровней колебательного или вращательного движения атомов в молекуле – ΔЕ = Е''- Е'. Если Е^' > Е^'', то переход молекулы из состояния Е^'' в состояние Е^' сопровождается возрастанием энергии рассеянного фотона – и ν_ф > ν₀. Если Е^' < Е^'', то энергия рассеянного фотона станет и .

При обычных температурах подавляющее большинство молекул находится в основном состоянии, поэтому более вероятными являются переходы на уровни с большей энергией. Это значит, что в спектре рассеяния интенсивность линий, соответствующих «красным» спутникам будет больше, чем для «фиолетовых».

Исследование спектров комбинационного рассеяния позволяет судить о строении молекул, о характере симметрии молекул, определить собственные частоты колебаний атомов, осуществлять анализ сложных молекулярных смесей и, особенно, молекул органических.