МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ИЖЕВСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ
АКАДЕМИЯ»
Кафедра физики
Лаборатория механики и молекулярной физики №1(213а)
ЛАБОРАТОРНАЯ РАБОТА №2
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
Отредактировал: Кораблев Г.А.
Ижевск 2013
ЛАБОРАТОРНАЯ РАБОТА № 2
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
Цель работы: изучение колебаний математического или оборотного физического маятника, измерение периода его колебаний, определение ускорения свободного падения.
Приборы и принадлежности: 1) физический и математический маятники, 2) электросекундомер, 3) измерительная линейка, 4) призма.
Ускорением свободного падения называется ускорение, с которым движется свободно падающее тело. Численное значение зависит от географической широты и от высоты над поверхностью Земли и может быть измерено при помощи физического или математического маятника.
Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити, которая может совершать колебания около положения равновесия под действием возвращающей силы.
Практической моделью математического маятника служит массивное тело малых размеров, подвешенное на достаточно длинной тонкой нити. Если вывести маятник из положения равновесия (среднее положение на рис. 1), то под действием возвращающей силы он возвратиться положение равновесия. Если сопротивление движению отсутствует, то маятник будет совершать незатухающие колебания около положения равновесия.
Согласно закону динамики вращательного движения момент возвращающей силы, равной произведению ее касательной (тангенциальной) составляющей на расстояние до оси вращения, равен произведению момента инерции материальной точки на ее угловое ускорение момента инерции материальной точки 
на ее угловое ускорение 
. (1)
Знак минус показывает, что направление силы противоположно отклонению.
Для малых углов 
и из уравнения (1) получим дифференциальное уравнение колебаний
(2)
где обозначено 
.
 | |||
 |
Рис. 1
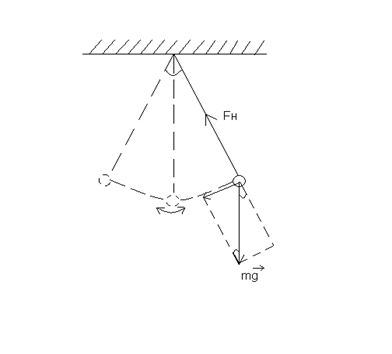
Физическим маятником называется твердое тело, способное совершать колебания под действием силы тяжести вокруг неподвижной оси, не совпадающей с его центром масс. Лабораторный физический маятник представляет собой стержень с утяжелённым одним или обоими концами. Ось подвеса изготавливается в виде призмы.
Если вывести маятник из положения равновесия на некоторый угол 
, то под действием силы F, равнодействующей сил 
и силы тяжести P маятник возвратится в положение равновесия, затем по инерции отклонится в противоположную сторону, вновь вернётся в положение равновесия и т. д. Если трение в подвесе и сопротивление среды не велико, то маятник будет колебаться практически без затухания. Центр масс маятника С будет описывать дугу окружности (см. рис. 2) радиуса ВС=d, равному расстоянию от центра масс до точки подвеса.
|
|
положительным при отклонении маятника вправо от положения равновесия, отрицательным – при отклонении влево. Касательная составляющая
(тангенциальная) возвращающей силы 
, где m – масса маятника. Знак минус показывает, что направление силы и угла всегда противоположны. При малых отклонениях и 
. Согласно основному закону динамики вращения момент силы
(3)
равен произведению момента инерции I тела относительно оси вращения на угловое ускорение .
Из уравнения (3) получим дифференциальное уравнение малых колебаний физического маятника в виде (2), где обозначено
(4)
Как видно, уравнение (2) имеет один и тот же вид, как для математического, так и для физического маятников. Его решение:
(5)
удовлетворяет уравнению (2), что можно проверить простой подстановкой 
.
Это решение описывается периодической функцией
период которой 
, 
носит название круговой (угловой) или циклической частоты, максимальное отклонение от положения равновесия 
называется амплитудой колебаний, 
– фаза колебания, 
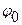– начальная фаза.
Скорость движения центра масс можно определить через произведение угловой скорости движения на расстояние до оси вращения
Период колебаний математического маятника (т.е. время одного полного колебания)
. (6)
Отсюда нетрудно получить выражение: 
, (7)
которое позволяет определить ускорение свободного падения по измеренным значениям длины l и периода колебаний математического маятника Тм.
Для определения ускорения свободного падения с помощью оборотного физического маятника поступим следующим образом.
По теореме Штейнера момент инерции маятника относительно одной из точек подвеса 
, а период его колебаний
, (8)
где 
– момент инерции относительно центра масс,
d1 – расстояние от центра масс до первой точки подвеса.
Момент инерции перевёрнутого маятника 
,
где d2 – расстояние от центра масс до второй точки подвеса, а его период колебаний, соответственно будет равен:
(9)
Важно исключить 
, определяя его из формулы (8), приравнивая к , полученному из формулы (9):
= 
,
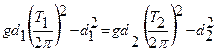Откуда сразу следует выражение для определения ускорения свободного падения по измеренным значениям периодов колебаний Т1 и Т2 прямого и перевёрнутого маятника и расстояниям d1 и d2 от центра масс до двух точек подвеса:
(10)
В данной работе используется установка, изображённая на рис. 3. Настенный кронштейн (1), на котором смонтирована подушка (2), опора призм и креплений нитей (3) бифилярного подвеса математического маятника. На опорной призме (4) подвешен физический маятник, который при перемене точки подвеса (4) и (5) превращается в оборотный маятник. На металлическом стержне между опорными призмами жёстко закреплена чечевица (6), а чечевица (7) может перемещаться по шкале (8) и закрепляться в нужном положении винтом (9).
Математический маятник выполнен в виде свинцового шарика (10), подвешенного бифилярно на капроновой нити. Изменение длины бифилярного подвеса производится барабанчиком (12). Фиксация барабанчика достигается винтом (11).
ЗАДАНИЕ №1
