Определение концентрации раствора сахара при помощи сахариметра.
Методические указания к лабораторной работе №9
по физике
(Раздел <<Оптика>>)
Ростов – на – Дону
Составители: В.С. Ковалева, А.П. Кудря, Н. Н. Фролова
УДК 530.1
Определение концентрации раствора сахара при помощи сахариметра.: Метод. указания.- Ростов н/Д: Издательский центр ДГТУ, 2011.- 10с
Методические указания содержат краткое описание процесса распространения линейно поляризованного света в оптически активных веществах.
Методические указания предназначены для студентов инженерных специальностей всех форм обучения, в программу учебного курса которых входит выполнение лабораторных работ по физике (раздел <<Оптика>>).
Печатается по решению методической комиссии факультета
<<Нанотехнологии и композиционные материалы>>
Рецензент доцент каф. физики, к.ф.-м.н. ЛЕМЕШКО Г.Ф.
©Издательский центр ДГТУ, 2011
Лабораторная работа № 9
Определение концентрации раствора сахара при помощи поляриметра
Цель работы: 1) рассмотреть процесс распространения линейно поляризованного света в оптически активных веществах;
2) определить концентрацию растворов сахара.
Оборудование: сахариметр, набор трубок с растворами сахара разной концентрации.
Теоретическая часть
Свет – это электромагнитные волны определенного диапазона длин волн. Электромагнитные волны поперечны: векторы напряженностей электрического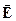 
и магнитного 
полей волны взаимно перпендикулярны и колеблются синфазно перпендикулярно вектору скорости 
распространения волны (перпендикулярно лучу). Эмпирически установлено, что физиологическое, фотоэлектрическое и другие действия света вызываются колебаниями вектора напряженности электрического поля 
, который называется в оптике световым вектором.
Свет, который можно представить как совокупность световых векторов , равновероятно ориентированных по всем направлениям, называется естественным.
Свет, в котором направления колебаний светового вектора каким- либо образом упорядочены, называется поляризованным.
Свет, в котором вектор колеблется только в одном направлении, перпендикулярном лучу, называется линейно поляризованным.
Плоскость, в которой колеблется световой вектор , называется плоскостью колебаний или плоскостью поляризации (рис. 1).
Различают свет поляризованный в плоскости, по кругу, по эллипсу или частично поляризованный.
Линейно поляризованный свет можно получить из естественного с помощью приборов, называемых поляризаторами.
Устройство, позволяющее анализировать свет, вышедший из поляризатора, называется анализатором. Поляризатор и анализаторвзаимозаменяемы. В качестве поляризатора и анализатора могут быть использованы поляроидные пленки, призмы Николя (николи) или другие устройства.
Плоскость, проходящая через поляризатор (анализатор) и в которой колеблется световой вектор 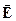, называется плоскостью поляризатора или главным сечением поляризатора (анализатора).
Если на скрещенные поляризатор и анализатор направить естественный свет, то из анализатора выходит доля света, согласно закону Малюса, пропорциональная квадрату косинуса угла между главными сечениями поляризатора и анализатора (см. рис. 1):
, (1)
где 
– интенсивность естественного света;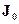 
– интенсивность поляризованного света (
, в силу двойного лучепреломления или явления дихроизма), 
– интенсивность света, прошедшего анализатор (рис. 1). Из закона Малюса следует, что если 
, то 
, т. е. поляризатор и анализатор скрещены или «поставлены на темноту», а если 
, то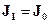 
- поляризатор и анализатор параллельны или «поставлены на свет», таким образом:
, а 
.
Оптически активными называются вещества, способные поворачивать плоскость поляризации света при прохождении его через такие вещества, как камфора, никотин, сахар, кварц и другие,
|
|
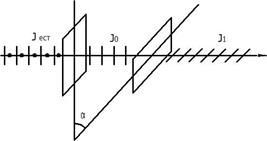
Рис. 1
имеющие асимметричное строение молекул.
Вращение плоскости поляризации было объяснено Френелем. Он предложил вектор линейно поляризованного света рассматривать как совокупность двух векторов 
и 
с левым и правым вращением. В обычных средах угловая скорость вращения векторов и одинакова, так что суммарный вектор 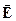в любой момент времени лежит в одной и той же плоскости (рис. 2).
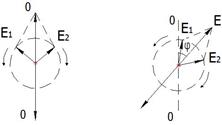
Рис. 2
В оптически активных веществах, благодаря особенности их структуры, угловые скорости вращения векторов и становятся разными, и по мере прохождения луча в оптически активной среде, вектор 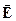будет отклоняться от начального положения на угол
, (2)
где 
- удельное вращение раствора, зависящее от природы оптически активного вещества и растворителя, длины волны света и температуры; 
- длина хода луча в веществе; 
- концентрация раствора оптически активного вещества.
Закономерность (2) используется в двух случаях.
1. По известным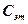 
, 
и 
определяют удельное вращение раствора
(3)
2. По известным 
, , 
определяют концентрацию
раствора оптически активного вещества
(4)
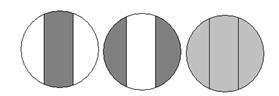
Между скрещенными поляризатором и анализатором (николями) помещают трубку с раствором оптически активного вещества (сахара). Поле зрения между николями, «поставленными
|
г
Рис. 3
|
|
|
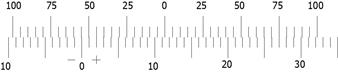
г
Рис. 4
на темноту», просветляется. Чтобы добиться полного гашения света, нужно анализатор повернуть вокруг луча на угол 
, равный углу вращения плоскости поляризации. Когда поле зрения окуляра равномерно затемнено рис. 3в (или рис. 4в), измеряем угол по шкале 3г (или рис. 4г).
Этот метод позволяет с достаточно большой точностью определять концентрации растворов оптически активных веществ, хорошо растворимых в воде, и широко используется в пищевой промышленности, медицине, криминалистике.