Пусть дана КС-грамматика G = (N, T, P, S). Рассмотрим предсказывающий разбор (или разбор сверху-вниз) для грамматики G.
Основная задача предсказывающего разбора - определение правила вывода, которое нужно применить к нетерминалу. Процесс предсказывающего разбора с точки зрения построения дерева разбора проиллюстрирован на рис. 4.1.

|
Фрагменты недостроенного дерева соответствуют сентенциальным формам. Вначале дерево состоит только из одной вершины, соответствующей аксиоме S. В этот момент по первому символу входной цепочки предсказывающий анализатор должен определить правило S  X1X2..., которое должно быть применено к S. Затем необходимо определить правило, которое должно быть применено к X1, и т.д., до тех пор, пока в процессе такого построения сентенциальной формы, соответствующей левому выводу, не будет применено правило Y
X1X2..., которое должно быть применено к S. Затем необходимо определить правило, которое должно быть применено к X1, и т.д., до тех пор, пока в процессе такого построения сентенциальной формы, соответствующей левому выводу, не будет применено правило Y  a.... Этот процесс затем применяется для следующего самого левого нетерминального символа сентенциальной формы.
a.... Этот процесс затем применяется для следующего самого левого нетерминального символа сентенциальной формы.
На рис. 4.2 приведена структура предсказывающего анализатора, который определяет очередное правило с помощью таблицы. Такую таблицу можно построить непосредственно по грамматике.

|
Таблично-управляемый предсказывающий анализатор имеет входную ленту, управляющее устройство (программу), таблицу анализа, магазин (стек) и выходную ленту.
Входная лента содержит анализируемую строку, заканчивающуюся символом $ - маркером конца строки. Выходная лента содержит последовательность примененных правил вывода.
Таблица анализа - это двумерный массив M[A, a], где A - нетерминал, и a - терминал или символ $. Значением M[A, a] может быть некоторое правило грамматики или элемент «ошибка».
Магазин может содержать последовательность символов грамматики с $ на дне. В начальный момент магазин содержит только начальный символ грамматики на верхушке и $ на дне.
Анализатор работает следующим образом. Вначале анализатор находится в конфигурации, в которой магазин содержит S$, на входной ленте w$ (w - анализируемая цепочка), выходная лента пуста. На каждом такте анализатор рассматривает X - символ на верхушке магазина и a - текущий входной символ. Эти два символа определяют действия анализатора. Имеются следующие возможности.
1. Если X = a = $, анализатор останавливается, сообщает об успешном окончании разбора и выдает содержимое выходной ленты.
2. Если X = a  $, анализатор удаляет X из магазина и продвигает указатель входа на следующий входной символ.
$, анализатор удаляет X из магазина и продвигает указатель входа на следующий входной символ.
3. Если X - терминал, и X  a, то анализатор останавливается и сообщает о том, что входная цепочка не принадлежит языку.
a, то анализатор останавливается и сообщает о том, что входная цепочка не принадлежит языку.
4. Если X - нетерминал, анализатор заглядывает в таблицу M[X, a]. Возможны два случая:
- Значением M[X, a] является правило для X. В этом случае анализатор заменяет X на верхушке магазина на правую часть данного правила, а само правило помещает на выходную ленту. Указатель входа не передвигается.
- Значением M[X, a] является «ошибка». В этом случае анализатор останавливается и сообщает о том, что входная цепочка не принадлежит языку.
Работа анализатора может быть задана следующей программой:
| do {X=верхний символ магазина; if (X - терминал || X=="$") if (X==InSym) {удалить X из магазина; InSym=очередной символ; } else error(); else /*X - нетерминал*/ if (M[X,InSym]=="X->Y1Y2...Yk") {удалить X из магазина; поместить Yk,Yk-1,...Y1 в магазин (Y1 на верхушку); вывести правило X->Y1Y2...Yk; } else error(); /*вход таблицы M пуст*/ } while (X!=$) /*магазин пуст*/ |
Пример 4.3. Рассмотрим грамматику арифметических выражений G = ({E, E', T, T', F}, {id, +, *, (,)}, P, E) с правилами:
E  TE' TE'
| T'  *FT' *FT'
| ||
E'  +TE' +TE'
| T'  e e
| ||
E'  e e
| F  (E) (E)
| ||
T  FT' FT'
| F  id id
| ||
Таблица предсказывающего анализатора для этой грамматики приведена на рис. 4.3. Пустые клетки таблицы соответствуют элементу «ошибка».

|
При разборе входной цепочки id + id * id$ анализатор совершает последовательность шагов, изображенную на рис. 4.4. Заметим, что анализатор осуществляет в точности левый вывод. Если за уже просмотренными входными символами поместить символы грамматики в магазине, то можно получить в точности левые сентенциальные формы вывода. Дерево разбора для этой цепочки приведено на рис. 4.5.

| ||

|
Функции FIRST и FOLLOW
При построении таблицы предсказывающего анализатора нам потребуются две функции - FIRST и FOLLOW.
Пусть G = (N, T, P, S) - КС-грамматика. Для  - произвольной цепочки, состоящей из символов грамматики, определим FIRST(
- произвольной цепочки, состоящей из символов грамматики, определим FIRST( ) как множество терминалов, с которых начинаются строки, выводимые из
) как множество терминалов, с которых начинаются строки, выводимые из  . Если
. Если 
 *e, то e также принадлежит FIRST(
*e, то e также принадлежит FIRST( ).
).
Определим FOLLOW(A) для нетерминала A как множество терминалов a, которые могут появиться непосредственно справа от A в некоторой сентенциальной форме грамматики, т.е. множество терминалов a таких, что существует вывод вида S  *
*  Aa
Aa 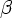 для некоторых
для некоторых  ,
, 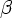
 (N
(N  T)*. Заметим, что между A и a в процессе вывода могут находиться нетерминальные символы, из которых выводится e. Если A может быть самым правым символом некоторой сентенциальной формы, то $ также принадлежит FOLLOW(A).
T)*. Заметим, что между A и a в процессе вывода могут находиться нетерминальные символы, из которых выводится e. Если A может быть самым правым символом некоторой сентенциальной формы, то $ также принадлежит FOLLOW(A).
Рассмотрим алгоритмы вычисления функции FIRST.
Алгоритм 4.3. Вычисление FIRST для символов грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FIRST(X) для каждого символа X  (N
(N  T).
T).
Метод. Выполнить шаги 1-3:
- Если X - терминал, то положить FIRST(X) = {X}; если X - нетерминал, положить FIRST(X) =
 .
. - Если в P имеется правило X
 e, то добавить e к FIRST(X).
e, то добавить e к FIRST(X). - Пока ни к какому множеству FIRST(X) нельзя уже будет добавить новые элементы, выполнять:
если X - нетерминал и имеется правило вывода X  Y 1Y 2...Y k, то включить a в FIRST(X), если a
Y 1Y 2...Y k, то включить a в FIRST(X), если a  FIRST(Y i) для некоторого i, 1
FIRST(Y i) для некоторого i, 1  i
i  k, и e принадлежит всем FIRST(Y 1),..., FIRST(Y i-1), то есть Y 1...Y i-1
k, и e принадлежит всем FIRST(Y 1),..., FIRST(Y i-1), то есть Y 1...Y i-1  *e. Если e принадлежит FIRST(Y j) для всех j = 1, 2,..., k, то добавить e к FIRST(X).
*e. Если e принадлежит FIRST(Y j) для всех j = 1, 2,..., k, то добавить e к FIRST(X).
Алгоритм 4.4. Вычисление FIRST для цепочки.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FIRST(X1X2...Xn), Xi  (N
(N  T).
T).
Метод. Выполнить шаги 1-3:
- При помощи предыдущего алгоритма вычислить FIRST(X) для каждого X
 (N
(N  T).
T). - Положить FIRST(X1X2...Xn) =
 .
. - Добавить к FIRST(X1X2...Xn) все не e-элементы из FIRST(X1). Добавить к нему также все не e-элементы из FIRST(X2), если e
 FIRST(X1), не e-элементы из FIRST(X3), если e принадлежит как FIRST(X1), так и FIRST(X2), и т.д. Наконец, добавить цепочку e к FIRST(X1X2...Xn), если e
FIRST(X1), не e-элементы из FIRST(X3), если e принадлежит как FIRST(X1), так и FIRST(X2), и т.д. Наконец, добавить цепочку e к FIRST(X1X2...Xn), если e  FIRST(Xi) для всех i.
FIRST(Xi) для всех i.
Рассмотрим алгоритм вычисления функции FOLLOW.
Алгоритм 4.5. Вычисление FOLLOW для нетерминалов грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FOLLOW(X) для каждого символа X  N.
N.
Метод. Выполнить шаги 1-4:
- Положить FOLLOW(X) =
 для каждого символа X
для каждого символа X  N.
N. - Добавить $ к FOLLOW(S).
- Если в P eсть правило вывода A

 B
B 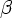 , где
, где  ,
, 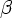
 (N
(N  T)* то все элементы из FIRST(
T)* то все элементы из FIRST(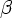 ), за исключением e, добавить к FOLLOW(B).
), за исключением e, добавить к FOLLOW(B). - Пока ничего нельзя будет добавить ни к какому множеству FOLLOW(X), выполнять:
если в P есть правило A 
 B или A
B или A 
 B
B 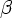 ,
,  ,
, 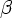
 (N
(N  T)*, где FIRST(
T)*, где FIRST(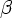 ) содержит e (т.е.
) содержит e (т.е. 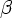
 *e), то все элементы из FOLLOW(A) добавить к FOLLOW(B).
*e), то все элементы из FOLLOW(A) добавить к FOLLOW(B).
Пример 4.4. Рассмотрим грамматику из примера 4.3. Для нее
| FIRST(E) = FIRST(T) = FIRST(F) = {(, id} | |
| FIRST(E') = {+, e} | |
| FIRST(T') = {*, e} | |
| FOLLOW(E) = FOLLOW(E') = {), $} | |
| FOLLOW(T) = FOLLOW(T') = {+,), $} | |
| FOLLOW(F) = {+, *,), $} | |
Например, id и левая скобка добавляются к FIRST(F) на шаге 3 при i = 1, поскольку FIRST(id) = {id} и FIRST(”(”) = {”(”} в соответствии с шагом 1. На шаге 3 при i = 1, в соответствии с правилом вывода T  FT' к FIRST(T) добавляются также id и левая скобка. На шаге 2 в FIRST(E') включается e.
FT' к FIRST(T) добавляются также id и левая скобка. На шаге 2 в FIRST(E') включается e.
При вычислении множеств FOLLOW на шаге 2 в FOLLOW(E) включается $. На шаге 3, на основании правила F  (E), к FOLLOW(E) добавляется также правая скобка. На шаге 4, примененном к правилу E
(E), к FOLLOW(E) добавляется также правая скобка. На шаге 4, примененном к правилу E  TE', в FOLLOW(E') включаются $ и правая скобка. Поскольку E'
TE', в FOLLOW(E') включаются $ и правая скобка. Поскольку E'  *e, они также попадают и во множество FOLLOW(T). В соответствии с правилом вывода E
*e, они также попадают и во множество FOLLOW(T). В соответствии с правилом вывода E  TE', на шаге 3 в FOLLOW(T) включаются и все элементы из FIRST(E'), отличные от e.
TE', на шаге 3 в FOLLOW(T) включаются и все элементы из FIRST(E'), отличные от e.






