Определение. Повторные (многократно повторяющиеся) испытания называются независимыми, по отношению к некоторому событию А, если вероятность появления события А в каждом из них не зависит от исходов других испытаний.
При повторных испытаниях вероятность появления события можно вычислить (в зависимости от условия задачи) по специальным формулам. Рассмотрим их:
4.1. Формула Бернулли. Теорема. Вероятность 
того, что некоторое событие появляется равно m раз в n независимых испытаниях равна 
Т.е. 
Здесь р и q- вероятность, соответственно, появления и не появления данного события в одном испытании, значит это полная система событий и потому р + q=1; 
- число сочетаний из n элементов по m.
Доказательство. Обозначим через 
появление события А в i- том испытании где i=1,2,…,n), а через 
- не появление события А в i-том испытании. Далее обозначим через р = 
. Пусть появится ровно m раз в n испытаниях и следовательно 
появится n-m раз.
Очевидно может появиться в различных комбинациях с- .Рассмот-
рим сумму таких возможных комбинаций (несовместных событий).
Очевидно, таких слагаемых будет , а каждое из них, будучи вероятностью произведения независимых событий, равно 
Значит искомая вероятность выразится равенством. 
Впредь желательно помнить, что: 
.
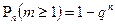Задача. Вероятность попадания в цель в каждом из пяти выстрелов есть р=0,8. Найти вероятность того, что будет ровно 2 попадания.
Дано: n=5, m=2, р=0.8, q=0,2. Найти 
(2)
Решение. 
, где по формуле 
будет 
Теперь 
4.2. Формула Пуассона. (Закон редких явлений). Вычислять, по формуле Бернулли, вероятность появления события при большом n и малом р, очень трудоемко. В этом случае пользуются формулой Пуассона. Она имеет вид 
где а = n p
Вывод. Обозначив пр = а, и учитывая что 
а 
формулу Бернулли преобразуем так
Здесь очевидно при n 
все скобки (кроме той, что в числителе) стремятся к 1, а та, что в числителе (по формуле замечательного предела, т.е. по формуле 
=е) примет вид 
Значит, при 
будет справедливо следующее приближенное равенство: 
.
Задача. Торговая база получила 10000 электролампочек. Вероятность повреждения электролампочки в пути равна 0,0001. Определить вероятность того, что в пути будет повреждено 4 электролампочки.
Решение. По условию имеем: m=4, n=10000, р=0,0001. Здесь, налицо, закон редких явлений (n - велико, р - мало). Значит, решать целесообразно по формуле Пуассона.
Получим (учитывая, что а = nр = 
=1)
4.3. Локальная теорема Лапласа. Если вероятность появления некоторого события в каждом из n независимых повторных испытаний постоянна и равна р, то вероятность того, что это событие появится ровно m раз в каждом из n испытаний определяется (для больших n и m) следующей формулой: Pn(m)≈ 
, где х=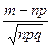 
, 
.
Для этой функция составлены специальные таблицы, они имеются в конце каждого учебника теории вероятностей. Кстати в этих таблицах значения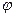 
(х) даны только для х>0, для значений х<0 следует воспользоваться тем что 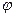(х) - четная функция, ведь 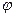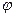(-х) = (х).
Задача. Вероятность поражения цели при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
Решение. Здесь n=100, m=75, p=0.8, 
