Н-образной подушки
 - деформация нижних приливов, определяемая по формуле (8.39).
- деформация нижних приливов, определяемая по формуле (8.39).
В случае установки среднего валка с использованием нижнего прилива и Н-образной подушки (см. рис. 8.2,б), при прокатке в верхнем горизонте, деформация станины определяется уравнением (8.40), а при прокатке в нижнем горизонте по уравнению
 . (8.41)
. (8.41)
В этом уравнении  +
+ 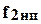 - упругая деформация нижней поперечины станины, определяемая по формуле (8.34);
- упругая деформация нижней поперечины станины, определяемая по формуле (8.34);  - удлинение стоек, рассчитываемое по формуле (8.27) или (8.30);
- удлинение стоек, рассчитываемое по формуле (8.27) или (8.30); 
 - упругое сжатие стоек Н-образной подушки, рассчитываемое по закону Гука
- упругое сжатие стоек Н-образной подушки, рассчитываемое по закону Гука
 , (8.42)
, (8.42)
где h и F - соответственно высота и площадь поперечного сечения стойки подушки, а Е - модуль упругости материала подушки;  - деформация стяжных болтов или крепежных клиньев крышки, рассчитываемая соответственно по формуле (8.36) или (8.37).
- деформация стяжных болтов или крепежных клиньев крышки, рассчитываемая соответственно по формуле (8.36) или (8.37).
Упругая деформация вспомогательных деталей клети
Упругая деформация (обычно сжатия) вспомогательных деталей рабочей клети, таких как прокладки, крепежные клинья, предохранительные уст-
ройства и подобных им, определяется по формуле:
 (8.43)
(8.43)
где Р - усилие, воспринимаемое деталью; Н и F - соответственно высота и площадь поперечного сечения детали; Е - модуль упругости материала детали.
Пример расчета коэффициента жесткости клети
Требуется определить коэффициент жесткости рабочей клети кварто 1700 тонколистового стана холодной прокатки. Конструкция и размеры клети представлены в монографии [2] на рис. III-40 и приводятся ниже при расчете отдельных узлов. Усилие прокатки равно 20 МН.
1. Рассчитаем упругую деформацию опорных валков. Валки имеют размеры, показанные на рис. 8.3. Материал опорных и рабочих валков сталь марки 9Х2МФ, модуль упругости примем Е =2.15×105 МПа, модуль сдвига - G =0.79 105 МПа [9].

Рис. 8.3. Конструкция и размеры валкового узла рабочей клети 1700
Составляющие прогиба опорного валка рассчитываем по формулам (8.4) и (8.5):
 0.47×10-3 м,
0.47×10-3 м,
 0.23×10-3 м.
0.23×10-3 м.
Рассчитаем приведенный радиус опорного и рабочего валков при радиусе опорного валка 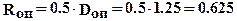 м и радиусе рабочего валка
м и радиусе рабочего валка  м:
м:
 м.
м.
Поскольку валки изготовлены из одного материала, приведенный модуль упругости будет равен  .
.
Рассчитаем упругое сплющивание валков на контакте опорного и рабочего валков по формуле (8.6) при L0 = 1.7 м:
 0.36×10-3 м.
0.36×10-3 м.
Таким образом общая деформация валков в соответствии с выражением (8.3), составит
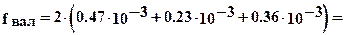 2.12 10-3 м.
2.12 10-3 м.
2. Рассчитаем упругую деформацию подушек. Величину деформации подушки опорного валка из литой стали с размерами, показанными на рис. 8.3, определяем по формуле (8.11) при Е=2.0×105 МПа:
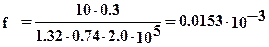 м.
м.
Одновременная деформация двух подушек будет равна
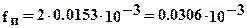 м.
м.
3. Рассчитаем упругую деформацию подшипников опорных валков. На стане применены четырехрядные роликовые подшипники с коническими роликами (см. рис. 8.3). Диаметр роликов подшипников опорных валков  = 110 мм, количество роликов в одном ряду - 24. По формуле (8.15), деформация подшипника составит
= 110 мм, количество роликов в одном ряду - 24. По формуле (8.15), деформация подшипника составит
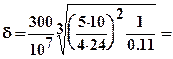 0.040×10-3 м.
0.040×10-3 м.
Суммарная деформация двух подшипников будет равна
 0.040×10-3=0.080×10-3 м.
0.040×10-3=0.080×10-3 м.
|
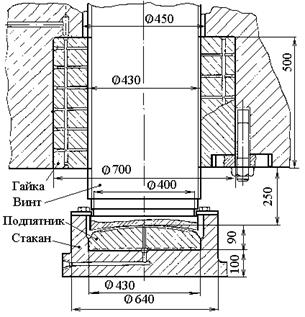
Рис. 8.4. К расчету деформации





 =1.15×105 МПа [9]. Величину упругой деформации гайки рассчитаем по формуле (8.21):
=1.15×105 МПа [9]. Величину упругой деформации гайки рассчитаем по формуле (8.21):
 = 0.231×10-3 м .
Деформацию винта рассчитываем по формуле (8.22), приняв модуль упругости
= 0.231×10-3 м .
Деформацию винта рассчитываем по формуле (8.22), приняв модуль упругости  =2.15×105 МПа:
=2.15×105 МПа:
 м.
м.