Проецирование многогранников

Рецензент

Морозов И.В. канд. техн. наук, доцент кафедры

Начертательной геометрии и графики ИГАСУ

Содержание

Введение 4

1. Классификация поверхностей 5

2. Многогранники 6

2.1. Проецирование многогранников 9

2.1.1. Призма 10

2.4.2. Пирамида 15

3. Построение развёрток 19

4. Пересечение плоскости и прямой линии с многогранником 23

4.1. Пересечение плоскости с многогранником 23

4.2. Пересечение прямой с многогранником 28

5. Формулировка задания 33

6. Последовательность выполнения задания 33

Библиографический список 41

 

 

ВВЕДЕНИЕ

Мир поверхностей разнообразен и безграничен. Он простирается от элементарной, отличающейся простотой и математической строгостью плоскости до сложнейших, причудливых форм криволинейных поверхностей, не поддающихся математическому описанию.

Без преувеличения можно сказать, что по образованию форм и свойств, по своему значению при формировании различных геометрических фигур, по той роли, которую они играют в науке, технике, архитектуре, изобразительном искусстве, поверхности не имеют себе равных среди других геометрических фигур.

Естественно, что начертательная геометрия как наука, не может обойти вниманием такие важные геометрические фигуры, какими являются поверхности.

 

 

 

КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ

Все поверхности можно подразделить на графические, закон образования которых нам неизвестен, и геометрические, закон которых известен.

Графическая поверхность, отнесённая к земной поверхности, изображённая на рис.1, называется топографической.

 

 

Рис.1

 

Поверхности геометрические могут образованы движением в пространстве прямой или кривой линии, которая называется образующей.

В зависимости от формы образующей поверхности делятся на линейчатые, когда образующей служит прямая (рис.2), и нелинейчатые, когда образующей служит кривая (рис. 3), например, поверхность тора.

По признаку развёртывания поверхности могут быть развёртываемыми и неразвёртываемыми.

По признаку направляющих, которые могут быть ломаными, прямыми или кривыми, поверхности могут быть гранными или кривыми.

 

 

Если плоская фигура ограничивает многогранник, то поверхность будет граной, если плоские кривые правильной формы, то поверхности будут кривыми, причём, если в образовании участвуют окружности в качестве направляющих, то получаем поверхности вращения.

Часть пространства, ограниченная со всех сторон поверхностью, называется телом.

Рис.2

Рис.3

МНОГОГРАННИКИ

Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником.

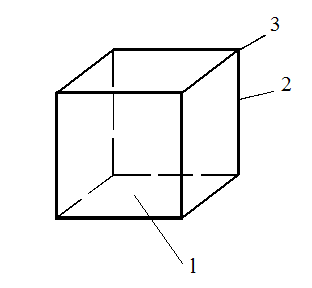
Плоские фигуры, ограничивающие многогранник, называются гранями 1 (рис.4). Грани пересекаются между собой по прямым линиям, которые называются рёбрами 2 многогранника. Рёбра пересекаются в точках – вершинах 3 многогранника. В каждой вершине сходятся не менее трёх рёбер.

 

 

 

Рис.4

 

 

Многогранники различают в зависимости от формы и количества граней.

В технике чаще встречаются следующие многогранники:

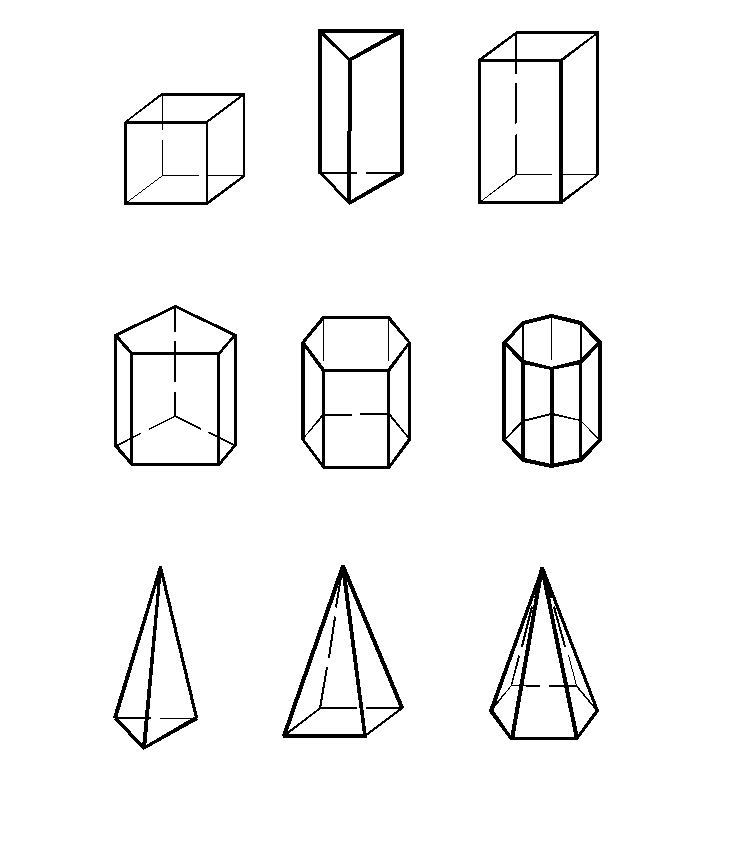
Многогранник, две грани которого конгруэнтны, а остальные пересекаются по параллельным прямым, называется призмой (рис.5, б-е). Название призмы зависит от того, какой многоугольник лежит в её основании, если треугольник, то и призма называется треугольной, если четырёхугольник, то призма будет четырёхугольной и т.д. Призма, основанием которой служит параллелограмм, называется параллелепипедом (рис.5,в). Прямоугольный параллепипед, все рёбра которого конгруэнтны между собой, называется кубом (рис.5,а).

Многогранник, одна грань которого, называется основанием, есть многоугольник, а остальные грани треугольники с общей вершиной, называется пирамидой (рис.5, ж, з, и).

Пирамиды и призмы могут быть правильными, если их основанием служит правильный многоугольник и высота проходит через его центр. У правильных многогранников все грани – равные правильные многоугольники и все двугранные углы его конгруэнтны.

 

а) б) в)

г) д) е)

ж) з) и)

Рис.5

Проецирование многогранников

Построение проекций многогранника начинают с изображения всех его вершин. Соединив соответствующим образом, одноимённые проекции вершин, получают проекции рёбер и граней многогранника. При этом принято считать, что грани многогранника непрозрачные и поэтому отдельные рёбра невидимы и обводятся штриховой линией.

При решении вопроса видимости принимается следующее взаимное расположение: глаз наблюдателя, проецируемые элементы, плоскость проекций. Отсюда следует, что видимым будет тот элемент, который будет дальше от плоскости проекций и тем самым ближе к наблюдателю. Из двух точек А и В (рис.6), расположенных на одном фронтально проецирующем луче, видимой является точка А; точка В расположена за точкой а и, следовательно, невидима.

 

Рис.6

 

При проецировании многогранников большую помощь в понимании его устройства может оказать формула Эйлера:

Г + В – Р = 2

где: Г – число граней;

В – число вершин;

Р – число рёбер.

 

Призма

Задача. Спроецировать прямую четырёхугольную призму на три взаимно перпендикулярные плоскости П1, П2 и П3 (рис.7,а).

 

 

Рис.7,а

 

Предварительный анализ:

1. Рёбра АВ, CL, EF и KD расположены перпендикулярно фронтальной и параллельно горизонтальной плоскости проекций. Каждое из этих рёбер спроецируется на фронтальную плоскость проекций в виде точки, а на горизонтальную плоскость проекций в виде прямых, перпендикулярных к оси проекций ОХ.

2. Грани АBEF и CDKL перпендикулярны фронтальной и горизонтальной плоскостям проекций, и они спроецируются на обе плоскости проекций в виде прямых, перпендикулярных к оси проекций ОХ.

3. Грани BDLF и FCKD конгруэнтны и параллельны фронтальной и перпендикулярны горизонтальной плоскостям проекций, в силу чего эти грани проецируются на фронтальную плоскость в виде фигуры, равной данным граням, а на горизонтальную плоскость - в виде прямых, параллельных оси проекций ОХ.

4. Верхняя грань ABLC, равная грани EKDF, проецируется в такую же равную фигуру на горизонтальную плоскость проекций.

5. Рёбра AE, BF, CK и DL, расположенные перпендикулярно горизонтальной плоскости проекций, спроецируются на неё в виде точек, а рёбра AC, BL, EK, FD, расположенные параллельно фронтальной и горизонтальной плоскостям проекций, проецируются в натуральную длину в виде отрезков, равных данным.

 

 

 

 

Рис.7,б

Проанализировав таким образом положение всех рёбер и граней призмы, перейдём к вычерчиванию проекций (рис.7,б)

Решение:

1. На фронтальной плоскости проекций (вид по стрелке S) грань призмы BDLF спроецируется в натуральный размер в виде прямоугольника (А2 ≡ В2, С2 ≡ D2, E2 ≡ F2, K2 ≡ L2). Задняя грань и передняя грань совпадут.

2. Аналогично находим горизонтальную проекцию призмы, которая изобразится в виде четырёхугольника, равного грани ABDC.

3. Нижнее основание и верхнее совпадут и дадут проекцию, у которой A1 ≡ E1, C1 ≡K1, D1 ≡L1, B1 ≡ F1.

4. По двум проекциям можно построить третью, для этого проведём под углом 45º постоянную чертежа, и с её помощью найдём все точки, проведя линии связи как с горизонтальной плоскости проекций, так и с фронтальной. В пересечении линий связи получим третью проекцию призмы (профильную).

Задача. Спроецировать шестиугольную призму на три плоскости проекций (рис.8,а).

Предварительный анализ:

1. Рёбра А1, В2, С3, D4, E5, F6 расположены перпендикулярно горизонтальной и параллельно фронтальной и профильной плоскости проекций. Каждое из этих рёбер спроецируется на горизонтальную плоскость проекций в виде точки, а на фронтальную и профильную плоскость проекций в виде прямых, перпендикулярных к оси проекций ОХ и ОY.

 

 

Рис.8,а

 

2. Грани BC23 и FE65 конгруэнтны* и параллельны фронтальной и перпендикулярны горизонтальной плоскостям проекций, в силу чего эти грани проецируются на фронтальную плоскость в виде фигуры, равной данным граням, а на горизонтальную плоскость – в виде прямых, параллельных оси проекций ОХ.

3. Верхняя грань ABCDEF, равная грани 123456, проецируется в такую же равную фигуру на горизонтальную плоскость проекций.

4. Рёбра ВС и FE, расположенные перпендикулярно профильной плоскости проекций, спроецируются на неё в виде точек, а на фронтальную плоскость проекций проецируются в натуральную длину в виде отрезков, равных данным.

 

Решение:

1. Вычерчиваем горизонтальную проекцию призмы, так как призма изо-

бразится на ней правильным шестиугольником. Проекции граней 123456 и ABCDEF на горизонтальной плоскости проекций совпадут.

2. На фронтальной плоскости проекций призма изобразится прямоугольником, разделённого на три части. Средняя часть определяет натуральную величину граней BC23 и FE65.

3. По двум проекциям строим третью проекцию (профильную).

_____________________________________________

* конгруэнтные фигуры (от лат. conqruens, родительный падеж conqruentis -

соответствующий, совпадающий), геометрические фигуры, переходящие

друг в друга при движении.

 

 

 

Рис.8,б

 

Пирамида

 

Задача 1. Построим три проекции пирамиды, так чтобы два ребра SA и SD были параллельны фронтальной плоскости проекций, а основание было параллельно горизонтальной плоскости (рис.9,а,б).

 

Предварительный анализ:

1. Рёбра SA и SD, как параллельные фронтальной плоскости, спроецируются на ней в натуральную длину, а на горизонтальной плоскости – в виде прямых, параллельных ОХ.

 

 

 

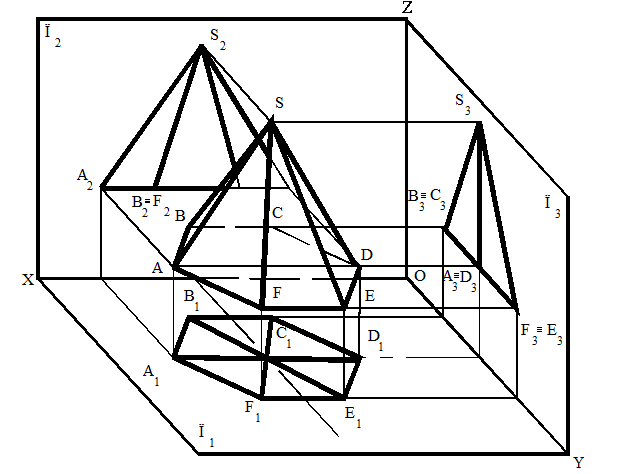
Рис. 9, а

 

2. Основание пирамиды спроецируется на плоскость П в натуральный размер, так как оно расположено параллельно горизонтальной плоскости проекций, а на фронтальную плоскость – в виде прямой, параллельной оси проекций.

3. Грани ASF, ASB, CSD и DSE находятся в общем положении, так как они наклонны ко всем плоскостям проекций.

4. Грани BSC и FSE перпендикулярны профильной плоскости проекций П3.

Рис. 9, б

Решение:

1. Начинаем вычерчивать с горизонтальной проекции, так как пирамида изобразится на ней правильным шестиугольником и линиями SA, SB, SC, SD, SE и SF, соединяющими вершину пирамиды S с точками основания.

 

2. На фронтальной плоскости проекций пирамиды изобразится в виде треугольника A2S2D2 и рёбер B2S2≡F2S2, C2S2≡E2S2, попарно и линий связи.

3. На фронтальной плоскости проекций пирамиды изобразится в виде треугольника A2S2D2 и рёбер B2S2≡ F2S2, C2S2≡ E2S2, попарно совмещённых.

4. Третья проекция строится при помощи постоянной прямой и линий связи.

 

Задача 2. На горизонтальной проекции пирамиды (см. рис.9) дана проекция L точки L. Требуется найти фронтальную проекцию данной точки.

Каждая точка находится при помощи прямой, лежащей в плоскости или образующей, так как точка, принадлежащая плоскости лежит на линии, принадлежащей также данной плоскости.

Решение:

1. Через горизонтальную проекцию L точки L проводим горизонтальную проекцию S1;

2. Находим её фронтальную проекцию S212;

3. На проекцию прямой S212 переносим проекцию L2 с помощью линии связи.

 

4. ПОСТРОЕНИЕ РАЗВЁРТОК

Плоская фигура, которая получается если поверхность тела разрезать по

ребру и совместить с плоскостью, называется развёрткой поверхности данного тела.

Развёртка многогранника получается последовательным совмещением с плоскостью всех граней.

Задача 1. На рис.10 изображена прямая треугольная призма АСА1В1С1. Построить развёртку призмы.

Предварительный анализ:

1. Разрезать поверхность призмы по рёбрам АА', АВ, АС, А'В и А'С'.

2. Совмести основание призмы и боковые грани АВВ'А' и САА'С' с плоскостью грани ВСС'В'.

3. Полученная фигура А'В'А'С'А'АСАВА будет развёрткой призмы.

Решение:

1. Проводим горизонтальную прямую и откладываем на ней три стороны основания призмы, длиной равной отрезку АВ, ВС, СА.

2. В точках А, В, С, А проводим перпендикуляры, на которых откладываем высоту призмы, взятой с фронтальной проекции. Отмечаем точки А', В', С', А'.

3. Из точек В и С проводим две дуги радиусом ВА и СА. Пересечение даст точку А.

4. Полученные точки соединяем.

 

 

Рис.10

Задача 2. На рис.11 показана прямая треугольная пирамида SABC. Построить развёртку пирамиды.

Предварительный анализ:

1. Разрезать поверхность пирамиды по рёбрам SC, CA, BC.

2. Совместим основание пирамиды АВС и боковые грани SAC и SBC

с гранью SAB.

3. Получим плоскую фигуру SCACBC которая будет развёрткой пира-

миды.

Решение:

1. На чертеже наносим точку S, из которой проводим дугу радиусом

равным натуральной длине ребра, например SA.

2. На дуге откладываем стороны основания пирамиды, равной нату-

ральной длине ребра АВ. Откладываем 3 стороны.

3. Из точки А и В проводим дуги радиусом АС.

4. Полученные точки соединяем.

 

 

 

 

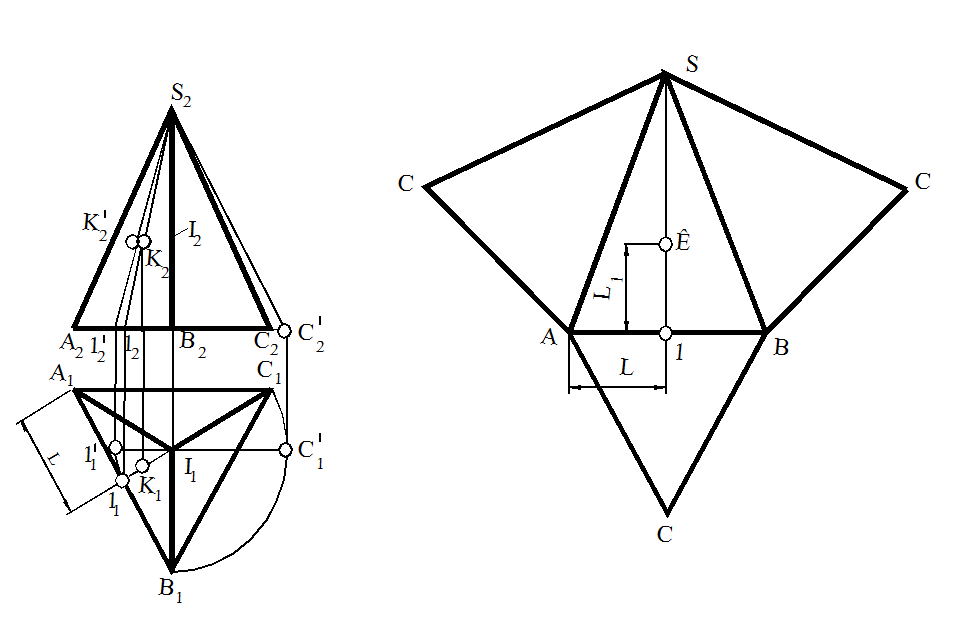
Рис.11