Агломеративная, или объединительная, кластеризация (agglomerative clustering)

Рис. 20.4. Классификация методов кластеризации

Разделяющая, или дивизивная, кластеризация (divisive clustering)

Иерархический метод кластеризации, при котором все объекты первоначально находятся в одном большом кластере. Кластеры формируют делением этого большого кластера на бо­лее мелкие.

Обычно в маркетинговых исследованиях используют агломеративные методы, например методы связи, дисперсионные и центроидные методы. Методы связи (linkage methods) вклю­чают метод одиночной связи, метод полной связи и метод средней связи.

Методы связи (linkage methods)

Агломеративные методы иерархической кластеризации, которые объединяют объекты в кластер, исходя из вычисленного расстояния между ними.

В основе метода одиночной связи (single method) лежит минимальное расстояние, или п вило ближайшего соседа.

Метод одиночной связи (single method)

Метод связи, в основе которого лежит минимальное расстояние между объектами, ил правило ближайшего соседа.

При формировании кластера первыми объединяют два объекта, расстояние между котор ми минимально. Далее определяют следующее по величине самое короткое расстояние, i кластер с первыми двумя объектами вводят третий объект. На каждой стадии расстояние мел двумя кластерами представляет собой расстояние между их ближайшими точками (рис. 20.5)

Среднее

расстояние
Кластер 1 Кластер 2

Рис. 20.5. Методы связи для процедуры кластеризации

На любой стадии два кластера объединяют по единственному кратчайшемурасстоянию is жду ними. Этот процесс продолжают до тех пор, пока все объекты не будут объединены в ю стер. Если кластеры плохо определены, то метод одиночной связи работает недостаточно хо{ шо. Метод полной связи (complete linkage) аналогичен методу одиночной связи, за исключен ем того, что в его основе лежит максимальное расстояние между объектами, или прави дальнего соседа. В методе полной связи расстояние между двумя кластерами вычисляют к расстояние между двумя их самыми удаленными точками.

Метод полной связи (complete linkage)

Метод связи, в основе которого лежит максимальное расстояние между объектами, ИЛ1 правило дальнего соседа.

Метод средней связи (average linkage) действует аналогично. Однако в этом методе рас­стояние между двумя кластерами определяют как среднее значение всех расстояний, изме->енных между объектами двух кластеров, при этом в каждую пару входят объекты из разных сластеров (см. рис. 20.5).

Метод средней связи (average linkage)

Метод связи, в основе которого лежит среднее значение всех расстояний, измеренных между объектами двух кластеров, при этом в каждую пару входят объекты из разных кластеров.

Из рис. 20.5 видно, что метод средней связи использует информацию обо всех расстояниях 1сжду парами, а не только минимальное или максимальное расстояние. По этой причине >бычно предпочитают метод средней связи, а не методы одиночной или полной связи.

Дисперсионные методы (variance methods) формируют кластеры таким образом, чтобы ми-шмизировать внутри кластерную дисперсию.

Дисперсионный метод (variance methods)

Агломеративный метод иерархической кластеризации, в котором кластеры формируют так, чтобы минимизировать внутрикластерную дисперсию.

Широко известным дисперсионным методом, используемым для этой цели, является метод Зарда (Ward's procedure).

Метод Варда (Ward's procedure)

Дисперсионный метод, в котором кластеры формируют таким образом, чтобы минимизиро­вать квадраты евклидовых расстояний до кластерных средних.

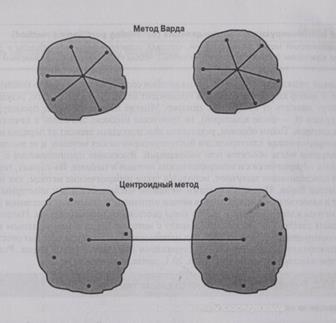
Для каждого кластера вычисляют средние всех переменных. Затем для каждого объекта вы-шсляют квадраты евклидовых расстояний до кластерных средних (рис. 20.6).

Эти квадраты расстояний суммируют для всех объектов. На каждой стадии объединяют два сластера с наименьшим приростом в полной внутри кластерной дисперсии. В центроидных ме-годах (centroid method) расстояние между двумя кластерами представляет собой расстояние ме-кду их центроидами (средними для всех переменных), как показано на рис. 20.6.

Центроидный метод (centroid method)

Дисперсионный метод иерархической кластеризации, в котором расстояние между двумя кластерами представляет собой расстояние между их центроидами (средними для всех пе­ременных).

Каждый раз объекты группируют и вычисляют новый центроид. Изо всех иерархических методов методы средней связи и Варда показывают наилучшие результаты по сравнению с дру-"ими методами [12].

К другому типу процедур кластеризации относятся неиерахические методы кластеризации nonhierarchical clustering), часто называемые методом А>средних.

Неиерархические методы кластеризации, метод k-средних (nonhierarchical clustering, k-means clustering)

Метод, который вначале определяет центр кластера, а затем группирует все объекты в пре­делах заданного от центра порогового значения.

Рис. 20.6. Другие агломеративные методы кластеризации

Эти методы включают последовательный пороговый метод, параллельный пороговый метод и оптимизирующее распределение. В последовательном пороговом методе (sequential threshold method) выбирают центр кластера и все объекты, находящиеся в пределах задан­ного от центра порогового значения, группируют вместе. Затем выбирают новый кластер­ный центр, и процесс повторяют для несгруппированных точек. После того как объект помещен в кластер с этим новым центром, его уже не рассматривают как объект для даль­нейшей кластеризации.

Последовательный пороговый метод (sequential threshold method)

Неиерархический метод кластеризации, при котором выбирают кластер и все объекты, на­ходящиеся в пределах заданного от центра порогового значения, группируют вместе.

Аналогично работает параллельный пороговый метод (parallel threshold method), за исключе­нием того, что одновременно выбирают несколько кластерных центров и объекты в пределах порогового уровня группируют с ближайшим центром.

Параллельный пороговый метод (parallel threshold method)

Неиерархический метод кластеризации, при котором одновременно определяют несколько кластерных центров. Все объекты, находящиеся в пределах заданного центром порогового значения, группируют вместе.

Метод оптимизирующего распределения (optimizing partitioning method) отличается от двух изложенных выше пороговых методов тем, что объекты можно впоследствии поставить в соот­ветствие другим кластерам (перераспределить), чтобы оптимизировать суммарный критерий, такой как среднее внутри кластерное расстояние для данного числа кластеров.

Метод оптимизирующего распределения (optimizing partitioning method)

Неиерархический метод кластеризации, который позволяет поставить объекты в соответствие другим кластерам (перераспределить объекты), чтобы оптимизировать суммарный критерий.

Два главных недостатка неиерархических методов состоят в том, что число кластеров определя­ется заранее и выбор кластерных центров происходит независимо. Более того, результаты класте­ризации могут зависеть от выбранных центров. Многие неиерархические процедуры выбирают первые k случаев (k — число кластеров), не пропуская никаких значений в качестве начальных кластерных центров. Таким образом, результаты кластеризации зависят от порядка наблюдений в данных. Неиерархическая кластеризация быстрее иерархических методов, и ее выгодно использо­вать при большом числе объектов или наблюдений. Высказано предположение о возможности использования иерархических и неиерархических методов в тандеме. Во-первых, первоначальное решение по кластеризации получают, используя такие иерархические методы, как метод средней связи или метод Варда. Полученное этими методами число кластеров и кластерных центроидов используют в качестве исходных данных в методе оптимизирующего распределения [13]. Выбор метода кластеризации и выбор меры расстояния взаимосвязаны. Например, квадра­ты евклидовых расстояний используют наряду с методом Варда и центроидным методом. Не­которые из неиерархических методов также используют квадраты евклидовых расстояний. Для иллюстрации иерархической кластеризации используем метод Варда. Результаты, по­лученные при кластеризации данных табл. 20.1, приведены в табл. 20.2.

Таблица 20.2. Результаты иерархической кластеризации

План агломерации на основании метода Варда

Объединяемые кластеры Стадия, на которой впервые появился кластер

Стадия Кластер 1 Кластер 2 Коэффициент (расстояние между Кластер 1 Кластер 2 Следующая объединяемыми кластерами) стадия

1 14 16 1,000000 007 2 2 13 2,500000 0 0 15 3 7 12 4,000000 0 0 10 4 5 11 5,500000 0 0 11 5 3 8 7,000000 0 0 16 6 1 6 8,500000 0 0 10 7 10 14 10,166667 0 1 9 8 9 20 12,666667 0 0 11 9 4 10 15,250000 0 7 12 Ю 1 7 18,250000 6 3 13 11 5 9 22,750000 4 8 15 12 4 19 27,500000 9 0 17 13 1 17 32,700001 10 0 14 14 1 15 40,500000 13 0 16 15 2 5 51,000000 2 11 18 16 1 3 63,125000 14 5 19 17 4 18 78,291664 12 0 18 18 2 4 171,291656 15 17 19 19 1 2 330,450012 16 18 0

Принадлежность кластеру при использовании метода Варда Число кластеров Метка (номер) случая 432

11 1 1 22 2 2 31 1 1 43 3 2 52 2 2 61 1 1 71 1 1 81 1 1 92 2 2 10 3 3 2 11 2 2 2 12 1 1 1 13 2 2 2 14 3 3 2 15 1 1 1 16 3 3 2 17 1 1 1 18 4 3 2 19 3 3 2 20 2 2 2

Полезную информацию можно извлечь из плана агломерации, где показано число случа«или кластеров, которые нужно объединить на каждой стадии. Первая строка представляет пе] вую стадию, когда есть 19 кластеров. На этой стадии объединены респонденты 14 и 16, что п< казано в колонках, озаглавленных "Объединяемые кластеры". Квадрат евклидовою расстояш между точками, соответствующими этим двум респондентам, дан в колонке "Коэффициет Колонка "Стадия, на которой впервые появился кластер" показывает стадию, на которой впе] вые был сформирован кластер. Например, цифра (входа в кластер) 1 на стадии 7 указывает \ то, что респондента 14 впервые включили в кластер на стадии 1. Последняя колонк "Следующая стадия", показывает стадию, на которой другой случай (респондент) или класт< объединили с этим кластером. Поскольку число в первой строке последней колонки равно значит, респондента 10 объединили с респондентами 14 и 16 на стадии 7, чтобы сформирова' один кластер. Аналогично, вторая строка представляет стадию 2 с 18 кластерами. На стадии респондентов 2 и 13 группируют вместе. Другая важная часть результата кластеризации содержится в сосульчатой диаграмме, пре, ставленной на рис. 20.7.

Столбики соответствуют объектам, которые подлежат кластеризации, в этом случае респон­дентам присвоили номера от 1 до 20. Ряды соответствуют числу кластеров. Эту диаграмму чи­тают снизу вверх. Вначале все случаи считают отдельными кластерами. Так как мы имеем 20 респондентов, количество исходных кластеров равно 20. На первой стадии объединяют два ближайших объекта, что приводит к 19 кластерам. Последняя строчка на рис. 20.7 показывает эти 19 кластеров. Два случая, а именно респонденты 14 и 16, которых объединили на этой ста­дии, не имеют между собой разделяющего пустого (белого) пространства. Ряд с номером 18 со­ответствует следующей стадии с 18 кластерами. На этой стадии вместе группируют респонден­тов 2 и 13. Таким образом на этой стадии мы имеем 18 кластеров, 16 из них состоят из отдель­ных респондентов, а два содержат по два респондента. На каждой последующей стадии формируется новый кластер одним из трех способов: два отдельных объекта группируют вме­сте; объект присоединяют к уже существующему кластеру; два кластера группируют вместе.

Еще одно полезное графическое средство отображения результатов кластеризации — это древовидная диаграмма (дендрограмма) (рис. 20.8).

Древовидную диаграмму читают слева направо. Вертикальные линии показывают класте­ры, объединяемые вместе. Положение линии относительно шкалы расстояния показывает рас­стояния, при которых кластеры объединили. Поскольку многие расстояния на первых стадиях объединения примерно одинаковой величины, трудно описать последовательность, в которой объединили первые кластеры. Однако понятно, что на последних двух стадиях расстояния, при которых кластеры должны объединиться, достаточно большие. Эта информация имеет смысл при принятии решения о количестве кластеров (см. следующий раздел).

Кроме того, если число кластеров определено, то можно получить информацию о принад­лежности к кластеру. Хотя эта информация следует и из сосульчатой диаграммы, табличная форма нагляднее. Табл. 20.2 содержит данные о кластерной принадлежности объектов, в зави­симости от принятого решения: два, три или четыре кластера. Информацию такого рода можно получить для любого числа кластеров, и она полезна при принятии решения о числе кластеров.