Неустойчивость задачи решения системы линейных уравнений на примере системы (2 × 2)

Корректность вычислительной задачи. Примеры корректных и некорректных задач.

10. Устойчивость вычислительной задачи. Примеры. Устойчивость задачи вычисления определённого интеграла и задачи численного дифференцирования.

Неустойчивость задачи решения системы линейных уравнений на примере системы (2 × 2).

12. Представление чисел в компьютере. Машинные константы.

Пример: Найти машинные константы компьютера с разрядной сеткой 2+6+4.

Записать в памяти компьютера величины

а = 300010, в = -101,17203105, с = 0,02237825.

 

13. Особенности машинной арифметики. Погрешности арифметических операций в компьютере.

Пример: Вычислить на пятиразрядном «компьютере» (в двоичной арифметике), сравнить с точным результатом:

а) 1/1000 + 1/1000+ 1/1000 + 2;

б) 2 + 1/1000 + 1/1000+ 1/1000;

в) 2 × 1/1000;

г) 2: (1/1000).

 

14. Обусловленность вычислительной задачи. Обусловленность задачи вычитания близких чисел. Обусловленность задачи вычисления кратных корней.

Пример: Вычислить коэффициент обусловленности

y = 2 – x x ₁ = 1,99, х ₂ = 1,999999.

 

15. Обусловленность вычислительной задачи.

Пример: Вычислить коэффициенты обусловленности корней

Р ₁₀(х) = (х – 1)(х – 2) … (х –10) = а ₁₀ х ¹⁰ + а ₉ х ⁹ + … + а ₁ х + а₀

в зависимости от а ₉.

 

16. Обусловленность вычислительной задачи.

Пример: Вычислить коэффициенты обусловленности корней

Р ₁₀(х) = (х – 1)(х – 2) … (х –10) = а ₁₀ х ¹⁰ + а ₉ х ⁹ + … + а ₁ х + а₀

в зависимости от а ₀.

 

17. Обусловленность задачи вычисления значений вещественных функций. Обусловленность вычисления элементарных функций tg(x), Cos (x), arctg(x), если

х → 0, х → 1, х → ∞.

 

18. Обусловленность задачи вычисления определённого интеграла.

Пример: Вычислить коэффициент обусловленности , .

 

19. Неустойчивость вычислительных алгоритмов. Неустойчивость вычисления алгоритма .

20.Чувствительность вычислительных алгоритмов к ошибкам округления. Чувствительность алгоритма вычисления частичной суммы ряда.

Пример: Вычислить погрешность суммирования в порядке возрастания и в порядке убывания слагаемых на компьютере пятиразрядной сеткой.

 

21. Чувствительность вычислительных алгоритмов к ошибкам округления. Чувствительность алгоритма вычисления е^х.

Пример: Вычислить погрешность значения e^x для x=-10 на компьютере пятиразрядной сеткой.

 

22. Лемма о сходимости одношаговых итерационных процессов (доказательство)

 

23. Обусловленность задачи вычисления простого корня. Радиус неопределённости.

Пример: Найти радиус неопределённости корней уравнения

(х² – 2 x) = 0.

 

24. Обусловленность задачи вычисления кратного корня.

Пример: Найти радиус неопределённости корней уравнения (х² – 2 x)² = 0.

 

25. Метод бисекции.

Пример. Вычислить бОльший корень уравнения (х – cos2 x)² = 0

методом бисекции с точностью ε = 10^-1

 

26. Сходимость метода простой итерации. Геометрический смысл метода.

 

27. Критерий окончания итерации процесса (доказательство).

Пример: Построить итерационную функцию для нахождения корней уравнения (х – cos2 x)² = 0 на отрезке [12;17].

 

28. Метод Ньютона (док-во)

 

29. Метод Ньютона. Критерий окончания.

Пример: Найти с точностью ε = 10^-2 корень уравнения 3 х – х ² = 0 методом Ньютона.

 

30. Модификации метода Ньютона.

Пример: Вычислить с точностью ε = 10^-1 больший корень уравнения

3 х – х ² =0 с помощью модифицированных методов. х ⁽⁰⁾ = 1.

 

31. Методы вычисления корня уравнения со сверхлинейной сходимостью

(метод Стефенсена, обратной квадратичной интерполяции).

Пример: Вычислить с точностью ε = 10^-1 больший корень уравнения

3 х – х ² =0, х ⁽⁰⁾ = 1.

 

32. Норма вектора, норма матрицы. Свойства норм.

Пример: Вычислить (оценить) нормы ||×|| ₁, ||×||₂, ||×||_¥

33. Обусловленность задачи решения системы линейных уравнений.

Пример: Оценить число обусловленности системы А* Х = В

 

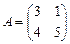
34. Обусловленность задачи решения системы линейных уравнений.

Пример: Вычислить число обусловленности матрицы

в норме ||×|| ₁, ||×||₂.

 

35. Метод Гаусса. Пример: Найти LU разложения матрицы

36. Анализ ошибок в методе Гаусса. Пример: Проанализировать погрешности решения системы методом Гаусса, если ε_м = 10^-3

 

37. Метод простой итерации для решения системы линейных уравнений.

Пример: Вычислить две итерации решения системы Ах = в

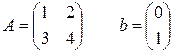х ⁽⁰⁾ = (0)

 

38. Метод простой итерации для системы нелинейных уравнений.

Пример: Исследовать сходимость метода простой итерации для системы

в области D =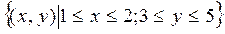

 

39. Метод Ньютона для систем нелинейных уравнений.

Пример: Вычислить три итерации метода для системы

 

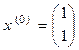
40.Аппроксимация функций. Интерполяция, экстраполяция. Единственность интерполяционного многочлена.

Пример: Вычислить значение интерполяционного многочлена Лагранжа третьей степени в точке х=3.21, оценить вычислительную погрешность. Значения функции заданы таблицей 1.

 

Таблица 1 – Значения функции в узлах.

xi	0,00	0,08	0,13	0,20	0,27	0,31	0,38	0,44
yi	1,00000	1,72539	1,97664	1,92950	1,45474	1,07307	0,42687	0,09338

 

 

41.Различные формы записи интерполяционных многочленов.

Пример: Вычислить значение интерполяционного многочлена Ньютона третьей степени в точке х=3.21, оценить вычислительную погрешность. Значения функции заданы таблицей 2.

 

Таблица 2 – Значения функции в узлах

х			х			х
0,1 0,2 0,3 0,4 0,5 0,6	1,00000 1,20500 1,42007 1,64538 1,88124 2,12815 2,38676	0,7 0,8 0,9 1,0 1,1 1,2 1,3	2,65797 2,94290 3,24293 3,55975 3,89537 4,25216 4,63285	1,4 1,5 1,6 1,7 1,8 1,9 2,0	5,04065 5,47918 5,95261 6,46561 7,02350 7,63219 8,29835

 

 

42. Погрешность интерполяции. (БЕЗ Док-ва)

Пример: Оценить погрешность представления функции e^x интерполяционным многочленом четвертой степени на отрезке [ 0,. 1 ], [100, 115].

 

43. Многочлены Чебышева Минимизация оценки погрешности интерполяции.(САМОСТОЯТЕЛЬНО!!!)

 

44. Плохая сходимость интерполяционного процесса по равноотстоящим узлам. Чувствительность интерполяционного многочлена к погрешностям входных данных и к ошибкам округления (понятие константы Лебега и числа обусловленности задачи вычисления интерполяционного полинома)

 

45. Локальная интерполяция. Сплайны.

 

46 Метод наименьших квадратов. САМОСТОЯТЕЛЬНО!!!)

Пример: Найти многочлен наилучшего приближения второй степени

для функции на отрезке .

 

47. Составные квадратурные формулы и оценки погрешности. Степень точности квадратурных формул. Формулы Ньютона – Котеса. САМОСТОЯТЕЛЬНО!!!)

Пример: Вычислить для n = 4 с помощью формул прямоугольников, трапеций, Симпсона. Оценить погрешность вычислений.

 

48. Квадратурные формулы Гаусса. Оценка погрешности. САМОСТОЯТЕЛЬНО!!!)

Пример: Вычислить для n = 2, 3 по формуле Гаусса, оценить погрешность.

 

49.Апостеорная оценка погрешности численного интегрирования. Правило Рунге оценки погрешности численного интегрирования. САМОСТОЯТЕЛЬНО!!!)

Пример: Оценить погрешность интегрирования, записать результат вычисления интеграла, если известно: I₄=12.452525, I₈=12.452552.

 

50. Численное дифференцирование. Формулу левых, правых центральных разностей.

Вычислить первую и вторую производную в точке x= 0,5 табл. Вопроса 43. САМОСТОЯТЕЛЬНО!!!)

 

51. Численное дифференцирование. Многоточечные формулы.

Вычислить первую и вторую производную в точке x= 1.546 (табл. 2).

САМОСТОЯТЕЛЬНО!!!)

52.. Оценка погрешности численного дифференцирования. Пример.

Вычислить первую и вторую производную в точке x= 1.546 (табл. 2). Оценить погрешность.

 

Не будет:

//53. Влияние погрешностей на вычисление производной.

//54. Улучшение погрешности в задаче вычисления производной.

 

// Rem: Примеры носят приблизительный характер.

В качестве эксперимента разрешу при подготовке шпаргалку формата а4 -- 1 шт.

Есть вопросы – задавайте.

Печать вопросов – 2 стр на лист