Представим себе, что имеются объекты различных видов, причем:
– всего имеется M видов объектов;
– объектов каждого i-го вида имеется Ni.
Тогда по Хартли, если мы извлекаем один из объектов i-го вида, то получаем Ii бит информации

|
В среднем по  на один объект i-го вида.
на один объект i-го вида.

|
Сумма этих средних будет равна:

|
(где: pi=1/Ni, – вероятность встречи объектов i-го вида).
Последнее выражение – это и есть формула Шеннона, которая, таким образом, позволяет рассчитать средневзвешенное количество информации, приходящееся на один объект, получаемое при предъявлении объектов различных видов.
Отметим, что идентификация объектов, как относящихся к тому или иному виду (i-му виду) осуществляется на основе признаков этих объектов. В простейшем варианте это может быть и один признак, например номер вида на бильярдном шаре, но в реальных случаях признаков может быть очень много и их различные наборы сложным и неоднозначным образом могут быть связаны с принадлежностью объектов к тем или иным классам.
Но главный вывод от этого не изменяется: формула Шеннона дает средневзвешенное количество информации, приходящееся на один объект, получаемое при предъявлении объектов различных видов (классов), отличающихся своими наборами признаков. Мера Шеннона является обобщением меры Хартли для неравновероятных событий.
13 Задача принятия оптимальных решений
Принятие решений есть постоянно решаемая в процессе управлениязадача. Трактовка принятия решения как задачи позволяет более четкосформулировать ее содержание, определить технологию и методы ее решения. Задача принятия решений (ЗПР) направлена на определение наилучшего (оптимального) способа действий для достижения поставленных целей. Под целью понимается идеальное представление желаемого состоянияили результата деятельности. Если фактическое состояние не соответствуетжелаемому, то имеет место проблема. Выработка плана действий поустранению проблемы составляет сущность задачи принятия решений. Проблемы могут возникать в следующих случаях:
- функционирование системы в данный момент не обеспечивает достижение поставленных целей;
- функционирование системы в будущем не обеспечит достижение поставленных целей;
- необходимо изменение целей деятельности.
Проблема всегда связана с определенными условиями, которыеобобщенно называют ситуацией. Совокупность проблемы и ситуации образуетпроблемную ситуацию. Выявление и описание проблемной ситуации даетисходную информацию для постановки задачи принятия решений.
Субъектом всякого решения является лицо, принимающее решение (ЛПР). Понятие ЛПР является собирательным. Это может быть одно лицо – индивидуальное ЛПР или группа лиц, вырабатывающих коллективноерешение, групповое ЛПР. Для помощи ЛПР в сборе и анализе информации иформировании решений привлекаются эксперты – специалисты по решаемойпроблеме. Понятие эксперта в теории принятия решений трактуется в широкомсмысле и включает сотрудников аппарата управления, подготавливающихрешение, ученых и практиков.
Принятие решений происходит во времени, поэтому вводится понятиепроцесса принятия решений. Этот процесс состоит из последовательностиэтапов и процедур и направлен на устранение проблемной ситуации. В процессе принятия решений формируются альтернативные (взаимоисключающие) варианты решений и оценивается ихпредпочтительность. Предпочтение – это интегральная оценка качестварешений, основанная на объективном анализе (знании, опыте, проведенииэкспериментов и расчетов) и субъективном понимании ценности, эффективности решений. Для осуществления выбора наилучшего решения индивидуальное ЛПР определяет критерий выбора. Групповое ЛПР производит выбор на основе принципа согласования. Конечным результатом ЗПР является решение, которое представляетсобой предписание к действию. С содержательной точки зрения решениемможет быть способ действия, план работы, вариант проекта и т.п. Решениеявляется одним из видов мыслительной деятельности и проявлением воличеловека и имеет свои характерные признаки, рассмотренные ранее. Решение называется допустимым, если оно удовлетворяет ограничениям:ресурсным, правовым, морально-этическим. Решение называется оптимальным (наилучшим), если оно обеспечивает экстремум (максимум илиминимум) критерия выбора при индивидуальном ЛПР или удовлетворяетпринципу согласования при групповом ЛПР.
Обобщенной характеристикой решения является его эффективность. Этахарактеристика включает эффект решения, определяющий степень достиженияцелей, и стоимость решения – совокупность затрат ресурсов для принятия иреализации решения. Таким образом, эффективность решения - это степеньдостижения целей, отнесенная к затратам на их достижение. Решение тем эффективнее, чем больше степень достижения целей и меньше стоимостьзатрат.
Несмотря на то, что методы принятия решений отличаются универсальностью, их успешное применение в значительной мере зависит от профессиональной подготовки специалиста, который должен иметь четкое представление о специфических особенностях изучаемой системы и уметь корректно поставить задачу. Искусство постановки задач постигается на примерах успешно реализованных разработок и основывается на четком представлении преимуществ, недостатков и специфики различных методов оптимизации. В первом приближении можно сформулировать следующую последовательность действий, которые составляют содержание процесса постановки задачи:
· установление границы подлежащей оптимизации системы, т.е. представление системы в виде некоторой изолированной части реального мира. Расширение границ системы повышает размерность и сложность многокомпонентной системы и, тем самым, затрудняет ее анализ. Следовательно, в инженерной практике следует к декомпозиции сложных систем на подсистемы, которые можно изучать по отдельности без излишнего упрощения реальной ситуации;
· определение показателя эффективности, на основе которого можно оценить характеристики системы или ее проекта с тем, чтобы выявить "наилучший" проект или множество "наилучших" условий функционирования системы. В инженерных приложениях обычно выбираются показатели экономического (издержки, прибыль и т.д.) или технологического (производительность, энергоемкость, материалоемкость и т.д.) характера. "Наилучшему" варианту всегда соответствует экстремальное значение показателя эффективности функционирования системы;
· выбор внутрисистемных независимых переменных, которые должны адекватно описывать допустимые проекты или условия функционирования системы и способствовать тому, чтобы все важнейшие технико-экономические решения нашли отражение в формулировке задачи;
· построение модели, которая описывает взаимосвязи между переменными задачи и отражает влияние независимых переменных на значение показателя эффективности. В самом общем случае структура модели включает основные уравнения материальных и энергетических балансов, соотношения, связанные с проектными решениями, уравнения, описывающие физические процессы, протекающие в системе, неравенства, которые определяют область допустимых значений независимых переменных и устанавливают лимиты имеющихся ресурсов. Элементы модели содержат всю информацию, которая обычно используется при расчете проекта или прогнозировании характеристик инженерной системы. Очевидно, процесс построения модели является весьма трудоемким и требует четкого понимания специфических особенностей рассматриваемой системы.
Все оптимизационные задачи имеют общую структуру. Их можно классифицировать как задачи минимизации (максимизации) M-векторного векторного показателя эффективности Wm(x), m=1,2,...,M, N-мерного векторного аргумента x=(x1,x2,...,xN), компоненты которого удовлетворяют системе ограничений-равенств hk(x)=0, k=1,2...K, ограничений-неравенств gj(x)>0, j=1,2,...J, областным ограничениям xli<xi<xui, i=1,2...N.
Все задачи принятия оптимальных решений можно классифицировать в соответствии с видом функций и размерностью Wm(x), hk(x), gj(x) и размерностью и содержанием вектора x:
- одноцелевое принятие решений - Wm(x) - скаляр;
- многоцелевое принятие решений - Wm(x) - вектор;
- принятие решений в условиях определенности - исходные данные - детерминированные;
- принятие решений в условиях неопределенности - исходные данные - случайные.
Наиболее разработан и широко используется на практике аппарат одноцелевого принятия решений в условиях определенности, который получил название математического программирования. Более подробно задачи линейного программирования (W(x), hk(x), gj(x) - линейны) изложены во второй части курсовой работы, нелинейного программирования (W(x), hk(x), gj(x) - нелинейны) - в 3 части, стохастического программирования - в 4 части.
Математический аппарат одноцелевого принятия решений в условиях неопределенности, представляет собой стохастическое программирование (известны законы распределения случайных величин), теории игр и статистических решений (закон распределения случайных величин неизвестен).
Рассмотрим процесс принятия решений с самых общих позиций. Психологами установлено, что решение не является начальным процессом творческой деятельности. Оказывается, непосредственно акту решения предшествует тонкий и обширный процесс работы мозга, который формирует и предопределяет направленность решения. В этот этап, который можно назвать "предрешением" входят следующие элементы:
· мотивация, то есть желание или необходимость что-то сделать. Мотивация определяет цель какого-либо действия, используя весь прошлый опыт, включая результаты;
· возможность неоднозначности результатов;
· возможность неоднозначности способов достижения результатов, то есть свобода выбора.
После этого предварительного этапа следует, собственно, этап принятия решения. Но на нем процесс не заканчивается, т.к. обычно после принятия решения следует оценка результатов и корректировка действий. Таким образом, принятие решений следует воспринимать не как единовременный акт, а как последовательный процесс.
Выдвинутые выше положения носят достаточно общий характер, обычно подробно исследуемый психологами. Более близкой с точки зрения инженера будет следующая схема процесса принятия решения. Эта схема включает в себя следующие компоненты:
· анализ исходной ситуации;
· анализ возможностей выбора;
· выбор решения;
· оценка последствий решения и его корректировка.
14 Задача линейного программирования
Задачи линейного программирования относятся к категории оптимизационных. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования. Несмотря на различные области приложения, данные задачи имеют единую постановку: найти значения переменных x1, …, xn, доставляющие оптимум заданной линейной формы z=c1x1 + c2x2+… + cnxn при выполнении системы ограничений, представляющих собой также линейные формы.
Линейное программирование - раздел теории оптимизации, посвященный изучению и решению экстремальных задач, в которых линейная функция и ограничения, задающие допустимое множество, являются линейными.
Слово «программирование» объясняется тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно определяют программу (план) действий некоторого объекта, например, промышленного предприятия. Слово «линейное» отражает линейную зависимость между переменными.
Простые ЗЛП допускают геометрическую интерпретацию, позволяющую непосредственно из графика получить решение и проиллюстрировать идею решения более сложных задач линейного программирования.
Графическое решение задачи приведено на рисунке 1.
Ограничения здесь задают область допустимых решений в форме (заштрихованного) четырехугольника, а семейство (пунктирных) прямых, представляет собой линии уровня целевой функции F.
Существует два крайних положения линии уровня, когда она «касается» допустимого множества. Этим двум положениям в данном случае соответствуют две точки «касания» -начало координат (0, 0) и точка (9, 13). Первая из этих точек - точка минимума, а вторая - максимума данной функции F вида (1) на допустимом множестве (2).

Рисунок 1 - Графическое решение ЗЛП
В случае большего числа разнородных ограничений графическая интерпретация задачи затруднена, поэтому задачу представляют в математической форме и используются специальные методы.
Постановка данной задачи выглядит следующим образом.
Имеется множество переменных X = (x1, х2,..., хn). Целевая функция линейно зависит от управляемых параметров:

Имеются ограничения, которые представляют собой линейные формы
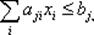 где
где  .
.
Задача линейного программирования формулируется так:
Определить максимум линейной формы F(x1,…,xn)=max(c1x1+…+cnxn) при условии, что точка (х1, х2,..., хn) принадлежит некоторому множеству D, которое определяется системой линейных неравенств

Любое множество значений (х1*, х2*,..., хn*), которое удовлетворяет системе неравенств задачи линейного программирования, является допустимым решением данной задачи. Если при этом выполняется неравенство
c1х1o+ c2 х2o+..+ cn хno ≥ c1х1+ c2 х2+..+ cn хn
для всего множества значений x1, х2,..., хn, то значение х1o..хno является оптимальным решением задачи линейного программирования.
Задачу линейного программирования удобно представлять в векторной форме, тогда она будет выглядеть следующим образом: найти max F(x) = max (cTx) при условии АХ ≤ Ро; Х≥0, где с = (с1,с2,..., сn) представляет собой n-мерный вектор, составленный из коэффициентов целевой функции, причем сT-транспонированная вектор-строка; х = (х1, х2,..., хn) - n-мерный вектор переменных решений;
P0- m-мерный вектор свободных членов ограничений;
Матрица А размером (m×n) - матрица, составленная из коэффициентов всех линейных ограничений:

Простые ЗЛП допускают геометрическую интерпретацию, позволяющую непосредственно из графика получить решение и проиллюстрировать идею решения более сложных задач линейного программирования.
Каноническая задача линейного программирования заключается в минимизации (максимизации) линейной целевой функции
F(x) = clx1+c2x2+... + cnxn при ограничениях
a11х1 +а12х2 +...+а1nхn=b1
а21х1 +а22х2 +...+а2nхn=b1…
…
аm1х1 +аm2х2 +...+аmnхn=b1
x1,x2,...,xn>0,
где с1,с2,...,сn - коэффициенты целевой функции, а b1,b2,...,bn - свободные члены, которые считаются неотрицательными.
Вектор X = (x1, х2,..., xn), удовлетворяющий ограничениям задачи ЛП, называется допустимым решением или планом. Допустимый план X*, при котором целевая функция задачи ЛП принимает максимальное (минимальное) значение, называется оптимальным планом.
Иными словами, каноническая задача линейного программирования (ЛП) состоит в нахождении среди всех решений выписанной выше системы линейных уравнений такого ее неотрицательного решения, на котором достигает своего минимального (максимального) значения линейная целевая функция z от и переменных.
В задаче линейного программирования общего вида вместо некоторых (всех) равенств в ограничениях записаны нестрогие неравенства в ту или другую сторону; при этом условие неотрицательности переменных может отсутствовать для части или же для всех переменных. Известно, что решение любой задачи линейного программирования может быть сведено к решению канонической задачи, представляемой в форме (1) или (4).
Линейное программирование (ЛП) первоначально развивалось как направление, разрабатывающее новые подходы к решению задач минимизации выпуклых функций на выпуклом множестве. Понятие целевой функции, удобное для приложений, сформировалось позднее.
Наиболее простым и распространенным методом решения канонической задачи линейного программирования до сих пор является симплекс-метод, предложенный в 40-е годы прошлого века Дж. Данцигом. Геометрически идею симплекс-метода в упрощенной форме можно выразить следующим образом. Допустимым множеством в задаче линейного программирования является некоторое многогранное множество n-мерного векторного пространства (в частном случае n = 2 - это выпуклый и не обязательно ограниченный многоугольник). Работа симплекс-метода начинается с некоторой начальной вершины (начального опорного плана) многогранного множества. Специальным образом выясняется, нет ли среди соседних вершин такой, в которой значение целевой функции лучше? Если такая вершина находится, то она и принимается за следующее приближение. После этого вновь исследуются соседние вершины для полученного приближения и т. д. до тех пор, пока не будет получена вершина, среди соседних вершин которой не существует вершины с лучшим значением целевой функции. Такая вершина является оптимальной. Она соответствует оптимальной точке (оптимальному решению) задачи линейного программирования.
В настоящее время разработан широкий круг различных численных методов решения задач линейного программирования, каждый из которых учитывает ту или иную специфическую особенность имеющейся задачи линейного программирования.
Кроме симплекс-метода имеются и другие методы решения специальных задач ЛП: метод потенциалов, Венгерский метод, двойственный симплекс-метод, метод обратной матрицы (модифицированный симплекс-метод) и др.
В настоящее время линейное программирование представляет собой область математики, посвященную разработке теории и численных методов решения экстремальных задач с линейными целевыми функциями и линейными ограничениями в виде систем равенств и/или неравенств. С применением линейного программирования решается широкий круг задач экономического характера: задачи о комплексном использовании сырья, рационального раскроя материалов, задачи загрузки оборудования, размещения заказов по однородным предприятиям, задачи о смесях, задачи текущего производственного планирования (статическая модель), задачи перспективного оптимального планирования, транспортная задача.
15 Задача нелинейного программирования
Нелинейное программирование - раздел теории оптимизации (теории экстремальных задач), посвященный исследованию и решению задач минимизации (максимизации), в которых целевая функция и ограничения не являются линейными. К нелинейному программированию относят квадратичное, дробное, выпуклое, дискретное, целочисленное и геометрическое программирование.
В общем виде задачу нелинейного программирования можно сформулировать так:
F (х)→min (max)
при условии
g(x)≤ 0,
где х - вектор искомых переменных; F (х) - целевая числовая функция; g(x) - вектор-функция системы ограничений.
При этом могут быть разные случаи: целевая функция - нелинейная, а ограничения - линейны; целевая функция - линейная, а ограничения (хотя бы одно из них) - нелинейные; целевая функция и ограничения нелинейные. Задачи условной оптимизации нелинейного программирования бывают двух типов: когда в ограничениях имеют место знаки равенства и знаки неравенства.
Решение задачи нелинейного программирования (поиск глобального минимума или максимума) состоит в отыскании таких значений переменных, подчиненных системе ограничений, при которых достигает минимума или максимума данная целевая функция.
При решении некоторых нелинейных задач иногда удается использовать линейную теорию. Для этого вводят допущение, что на том или ином участке целевая функция возрастает или убывает пропорционально изменению переменных. Такой подход называется методом кусочно-линейных приближений.
Нелинейные задачи с ограничениями в форме равенств нередко решаются с помощью введения функции Лагранжа.
Функция Лагранжа для функции имеет вид:

где  - вектор множителей Лагранжа.
- вектор множителей Лагранжа.
Среди большого числа вычислительных алгоритмов нелинейного программирования значительное место занимают различные варианты градиентных методов (метод проекции градиента, метод условного градиента и т. п.), методы штрафных функций, методы барьерных функций, метод модифицированных функций Лагранжа и др.
Универсального метода, позволяющего находить наиболее эффективным способом решение любой нелинейной задачи, не существует. Поэтому для каждой конкретной задачи, учитывая ее специфику, подбирают тот или иной наиболее подходящий метод (и алгоритм) решения.
Постановки задач нелинейного программирования. Задачи нелинейного программирования на практике возникают довольно часто, например, когда затраты растут непропорционально количеству закупленных или произведенных товаров. Хорошо известно, что чем больше партия закупаемого товара, тем меньше стоимость единицы продукта. Любому покупателю знакомо понятие розничных и оптовых цен. Рассмотрим конкретный пример, иллюстрирующий данную ситуацию.
Планирование производства продукции. На действующем предприятии планируется организовать выпуск новых видов продукции. Для организации производства необходимо приобретать сырье, стоимость которого колеблется в зависимости от спроса. Цены на готовую продукцию предприятия предполагаются стабильными.
Итак, необходимо провести исследования о производстве двух видов изделий, для которых планируется приобретение сырья, цена которого зависит от объема закупаемой партии и спроса на рынке на сырье данного типа. Цены же на продукцию предприятия утверждены с учетом реальной обстановки и должны сохраняться неизменными. Объемы производства предстоит определить исходя из анализа сырьевой проблемы и ограниченности производственных ресурсов.
Пусть х1, х2 - объемы производимой продукции 1-го и 2-го видов, с1, с2 - цена единицы продукции 1-го и 2-го видов соответственно. Затраты на приобретение и доставку сырья представляют собой нелинейную функцию, зависящую от объема закупаемого товара, f1(x1), f2(x2). Таким образом, экономическая рентабельность планируемых мероприятий оценивается формулой

Предприятие для производства новых видов продукции может выделить лишь часть своих мощностей, что накладывает дополнительные ограничения на максимальный объем выпуска новых видов изделий. Устанавливаются также лимиты на стоимость основных фондов (эксплуатация зданий, снабжение электроэнергией, амортизационные отчисления) в объеме b1, и стоимость производственных процессов (вспомогательные материалы, заработная плата, накладные расходы и др.) в объеме b2 Известно, что изготовление единицы продукции первого вида требует а11 затрат из основных фондов и а12 трудовых затрат, а единицы продукции второго вида затрат в размере а21 и а22 соответственно. Учет этих факторов приводит к условиям
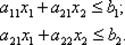
Теперь можно сформулировать задачу: определить такие х1, х2, которые бы обеспечивали максимум функционала

при ограничениях

x1,x2≤0
Таким образом, сформулирована задача, в которой целевая функция является нелинейной.
Квадратичное программирование - раздел нелинейного программирования, включающий совокупность методов решения экстремальных задач, в которых целевая функция представляет собой многочлен второй степени, а ограничения - линейные функции.
Задача квадратичного программирования может быть записана в матричной форме следующим образом:

где х - n-мерный вектор-столбец; х' - n-мерная вектор-строка; с' - n-мерная вектор-строка; b - m-мерный вектор-столбец; А - матрица размера m×n; D - симметрическая квадратная матрица порядка n;

Решить задачу квадратичного программирования это значит найти точку, для которой достигается максимум функции

где Ώ - множество допустимых планов задачи, определяемое системой ограничений Ах = b, х > 0.
Если D = 0, то задача сводится к задаче линейного программирования. Если целевая функция задачи квадратичного программирования ограничена сверху, то задача обязательно имеет оптимальное решение, т.е. точку глобального максимума.
Для нахождения глобального максимума общей задачи не существует эффективных вычислительных методов.
В настоящее время развиты методы выпуклого квадратичного программирования - раздела выпуклого программирования, который занимается задачами поиска глобального максимума выпуклой квадратичной функции на многогранном множестве. В этом классе задач доказано, что если матрица D является отрицательно определенной, то целевая функция будет ограничена сверху, и задача будет иметь оптимальное решение, и притом единственное.
Важное место в выпуклом квадратичном программировании занимает двойственная задача.
В соответствии с общим принципом двойственности для задачи двойственная задача имеет вид:

при условиях

где A’ - матрица, транспонированная по отношению к А; с - n-мерный вектор-столбец; λ - m-мерный вектор-столбец.
В линейном случае (при D = 0) определение двойственной задачи совпадает с принятым в линейном программировании.
Как и в случае линейного программирования в квадратичном программировании имеет место теорема двойственности:
если одна из задач двойственной пары разрешима, то и другая задача также разрешима; причем экстремальные значения обеих задач равны.
Условие Куна-Такера для выпуклой задачи имеет вид:
Ах = b;
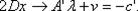

Таким образом, для того чтобы вектор х° был решением задачи, необходимо и достаточно существование вектора v° ≥ 0 и вектора λ0 таких, чтобы система векторов х°, v°, λ0 удовлетворяла условию. Любой (2n+m)-мерный вектор {х, v, λ.}, который является решением системы при условии х≥0, v≥0, будет крайней точкой многогранного множества, т.е. базисным решением системы:
Ах = b;
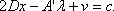
С учетом этого условия решение задачи квадратичного программирования сводится к нахождению базисных решений многогранных множеств, что может быть успешно осуществлено симплекс-методом линейного программирования за конечное число шагов.
Кроме общих методов выпуклого программирования специально для задачи выпуклого квадратичного программирования разработано большое количество численных методов, и в том числе конечных. Наиболее употребительными конечными методами являются: симплексный метод Билла, метод сопряженных градиентов, симплексный метод Вулфа. Эффективность того или иного метода существенно зависит от специфики решаемой задачи.
16 Задача стохастического программирования
В стохастическом программировании рассматриваются проблемы принятия решений в условиях действия случайных факторов, которые необходимо учитывать в соответствующих математических моделях.
Рассмотрим типичную задачу нелинейного программирования: найти такой вектор Х, для которого

при ограничениях
 ,
,

Задачи стохастического программирования возникают в случаях, когда функции  ,
,  зависят также от случайных параметров
зависят также от случайных параметров  . При этом предполагается, что
. При этом предполагается, что  является элементом пространства состояний природы (или пространства случайных параметров)
является элементом пространства состояний природы (или пространства случайных параметров)  . Тогда задачу стохастического программирования можно сформулировать так:
. Тогда задачу стохастического программирования можно сформулировать так:
Минимизировать  при условиях
при условиях
 ,
, 
Постановка задач стохастического программирования существенно зависит от того, есть ли возможность при выборе решений уточнить состояние природы  путем некоторых наблюдений или нет. В связи с этим различают задачи оперативного и перспективного стохастического программирования.
путем некоторых наблюдений или нет. В связи с этим различают задачи оперативного и перспективного стохастического программирования.
В задачах оперативного стохастического программирования решение принимается после некоторого эксперимента над состоянием природы  , оно зависит от результатов эксперимента и является случайным вектором
, оно зависит от результатов эксперимента и является случайным вектором  . Такие задачи возникают, например, в оперативном планировании, медицинской диагностике. В задачах перспективного стохастического программирования решение x принимается до проведения каких-либо наблюдений над состоянием природы и поэтому является детерминированным. Такие задачи возникают в перспективном технико-экономическом планировании, в задачах проектирования, когда параметры системы должны быть выбраны конкретными детерминированными величинами, в расчете на определенный диапазон возможных возмущений.
. Такие задачи возникают, например, в оперативном планировании, медицинской диагностике. В задачах перспективного стохастического программирования решение x принимается до проведения каких-либо наблюдений над состоянием природы и поэтому является детерминированным. Такие задачи возникают в перспективном технико-экономическом планировании, в задачах проектирования, когда параметры системы должны быть выбраны конкретными детерминированными величинами, в расчете на определенный диапазон возможных возмущений.
Задачи стохастического программирования обычно задаются в одной из следующих форм:
минимизировать 
при условиях (1)
 ,
,
где  – операция математического ожидания;
– операция математического ожидания;
минимизировать 
при ограничениях (2)
 ,
,
где 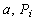 – некоторые числа;
– некоторые числа;
 – вероятность.
– вероятность.
Возможные и некоторые комбинации этих задач.
Например, найти минимум  при условиях
при условиях  или минимум
или минимум  при условиях
при условиях  . Несмотря на кажущееся различие в постановках задач, они могут быть сведены к некоторой общей формулировке. Для этого необходимо ввести характеристические функции:
. Несмотря на кажущееся различие в постановках задач, они могут быть сведены к некоторой общей формулировке. Для этого необходимо ввести характеристические функции:


для которых
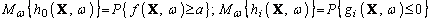
Задача (2) тогда приводится к виду
минимизировать 
при условии

Существует два основных подхода к решению задач стохастического программирования:
1) непрямые методы, которые заключаются в нахождении функций  ,
,  и решении эквивалентной задачи НП вида (1.6), (1.7);
и решении эквивалентной задачи НП вида (1.6), (1.7);
2) прямые методы стохастического программирования, основанные на информации о значении функций  ,
,  , получаемой в результате проведения экспериментов.
, получаемой в результате проведения экспериментов.
17 Автоматизированная система как сложная система с участием Л.П.Р.
Автоматизированная система - сложная система с определяющей ролью элементов двух типов:
- в виде технических средств;
- в виде действия человека.
Для сложной системы автоматизированный режим считается более предпочтительным, чем автоматический. Например, посадка самолета или захват дерева харвестерной головкой выполняется при участии человека, а автопилот или бортовой компьютер используется лишь на относительно простых операциях. Типична также ситуация, когда решение, выработанное техническими средствами, утверждается к исполнению человеком.
Структура системы - расчленение системы на группы элементов с указанием связей между ними, неизменное на все время рассмотрения и дающее представление о системе в целом. Указанное расчленение может иметь материальную, функциональную, алгоритмическую или другую основу. Пример материальной структуры - структурная схема сборного моста, которая состоит из отдельных, собираемых на месте секций и указывает только эти секции и порядок их соединения. Пример функциональной структуры - деление двигателя внутреннего сгорания на системы питания, смазки, охлаждения, передачи крутящего момента. Пример алгоритмической структуры - алгоритм программного средства, указывающего последовательность действий или инструкция, которая определяет действия при отыскании неисправности технического устройства.
Структура системы может быть охарактеризована по имеющимся в ней типам связей. Простейшими из них являются последовательное, параллельное соединение и обратная связь.
Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению какой-то цели.
Цель исследования операций - предварительное количественное обоснование оптимальных решений.
Всякий определенный выбор зависящих от нас параметров называется решением. Оптимальным называются решения, по тем или другим признакам предпочтительные перед другими.
Параметры, совокупность которых образует решение, называются элементами решения.
Множеством допустимых решений называются заданные условия, которые фиксированы и не могут быть нарушены.
Показатель эффективности - количественная мера, позволяющая сравнивать разные решения по эффективности.
Все решения принимаются всегда на основе информации, которой располагает лицо принимающее решение (ЛПР).
Каждая задача в своей постановке должна отражать структуру и динамику знаний ЛПР о множестве допустимых решений и о показателе эффективности.
Задача называется статической, если принятие решения происходит в наперед известном и не изменяющемся информационном состоянии. Если информационное состояние в ходе принятия решения сменяют друг друга, то задача называется динамической.
Информационные состояния ЛПР могут по-разному характеризовать его физическое состояние:
- Если информационное состояние состоит из единственного физического состояния, то задача называется определенной.
- Если информационное состояние содержит несколько физических состояний и ЛПР кроме их множества знает еще и вероятности каждого из этих физических состояний, то задача называется стохастической (частично неопределенной).
- Если информационное состояние содержит несколько физических состояний, но ЛПР кроме их множества ничего не знает о вероятности каждого из этих физических состояний, то задача называется неопределенной.
18 Принятие решений в условиях риска
В процессе принятия решений можно представить два крайних случая: определенность и неопределенность. В некоторых случаях неопределенность знаний является как бы "неполной" и дополняется некоторыми сведениями о действующих факторах, в частности, знанием законов распределения описывающих их случайных величин. Этот промежуточный случай соответствует ситуации риска. Принятие решений в условиях риска может быть основано на одном из следующих критериев:
- критерий ожидаемого значения;
- комбинации ожидаемого значения и дисперсии;
- известного предельного уровня;
- наиболее вероятного события в будущем.
Рассмотрим более подробно применение этих критериев.
a. Критерий ожидаемого значения (КОЗ).
Использование КОЗ предполагает принятие решения, обуславливающего максимальную прибыль при имеющихся исходных данных о вероятности полученного результата при том или другом решении. По существу, КОЗ представляет собой выборочные средние значения случайной величины. Естественно, что достоверность получаемого решения при этом будет зависеть от объема выборки. Так, если обозначить
КОЗ - Е(x1, x2,..., xn), (6.1)
где
x1, x2,..., xn - принимаемые решения при их количестве, равном n, то
E(xi) M(xi), (6.2)
где M(xi) - математическое ожидание критерия.
Таким образом, КОЗ может применяться, когда однотипные решения в сходных ситуациях приходится принимать большое число раз.
Приведем пример использования этого критерия для принятия решения.
b. Критерий "ожидаемого значения - дисперсия".
Как указывалось выше, КОЗ имеет область применения, ограниченную значительным числом однотипных решений, принимаемых в аналогичных ситуациях. Этот недостаток можно устранить, если применять комбинацию КОЗ и выборочной дисперсии s2. Возможным критерием при этом является минимум выражения
E(Z, ) = E(Z) k U(z), (6.5)
где
E(Z, ) - критерий "ожидаемого значения - дисперсия";
k - постоянный коэффициент;
U(Z) = mZ/S - выборочный коэффициент вариации;
mZ - оценка математического ожидания;
S - оценка среднего квадратического ожидания.
Знак "минус" ставится в случае оценки прибыли, знак "плюс" - в случае затрат.
Из зависимости (6.5) видно, что в данном случае точность предсказания результата повышается за счет учета возможного разброса значений E(Z), то есть введения своеобразной "страховки". При этом степень учета этой страховки регулируется коэффициентом k, который как бы управляет степенью учета возможных отклонений. Так, например, если для ЛПР имеет большое значение ожидаемые потери прибыли, то k>>1 и при этом существенно увеличивается роль отклонений от ожидаемого значения прибыли E(Z) за счет дисперсии.
c. Критерий предельного уровня.
Этот критерий не имеет четко выраженной математической формулировки и основан в значительной степени на интуиции и опыте ЛПР. При этом ЛПР на основании субъективных соображений определяет наиболее приемлемый способ действий. Критерий предельного уровня обычно не используется, когда нет полного представления о множестве возможных альтернатив. Учет ситуации риска при этом может производиться за счет введения законов распределений случайных факторов для известных альтернатив.
Несмотря на отсутствие формализации критерием предельного уровня пользуются довольно часто, задаваясь их значениями на основании экспертных или опытных данных.
d. Критерий наиболее вероятного исхода.
Этот критерий предполагает замену случайной ситуации детерминированной путем замены случайной величины прибыли (или затрат) единственным значением, имеющим наибольшую вероятность реализации. Использование данного критерия, также как и в предыдущем случае в значительной степени опирается на опыт и интуицию. При этом необходимо учитывать два обстоятельства, затрудняющие применение этого критерия:
- критерий нельзя использовать, если наибольшая вероятность события недопустимо мала;
- применение критерия невозможно, если несколько значений вероятностей возможного исхода равны между собой.
19 Методология принятия решений в условиях риска и неопределенности. Матрица решений
Методология принятия решения в условиях риска и неопределенности предполагает построение в процессе обоснования рисковых решений так называемой «матрицы решений», которая имеет следующий вид (табл. 1).
Таблица 1. «Матрица решений», выстраиваемая в процессе принятия решения в условиях риска или неопределенности
| Варианты альтернатив принятия решений | Варианты ситуаций развития событий | |||
| С1 | С2 | ... | С n | |
| А1 | Э11 | Э12 | ... | Э1 n |
| А2 | Э21 | Э22 | ... | Э2 n |
| ... | ... | |||
| А n | Э n1 | Э n2 | ... | Э nn |
В приведенной матрице значения A1; A2;... А n характеризуют каждый из вариантов альтернатив принятия решения; значения С 1; С2;...; С n — каждый из возможных вариантов ситуации развития событий; значения Э11; Э12; Э1 n; Э21; Э22; Э2 n; Э n1; Э n2;...; Э nn — конкретный уровень эффективности решения, соответствующий определенной альтернативе при определенной ситуации.
Приведенная матрица решений характеризует один из ее видов, обозначаемый как«матрица выигрышей», так как она рассматривает показатель эффективности. Возможно также построение матрицы решений и другого вида, обозначаемого как «матрица рисков», в котором вместо показателя эффективности используется показатель финансовых потерь, соответствующих определенным сочетаниям альтернатив принятия решений и возможным ситуациям развития событий.
На основе указанной матрицы рассчитывается наилучшее из альтернативных решений по избранному критерию. Методика этого расчета дифференцируется для условий риска и условий неопределенности.
Принятие решений в условиях риска основано на том, что каждой возможной ситуации развития событий может быть задана определенная вероятность его осуществления. Это позволяет взвесить каждое из конкретных значений эффективности по отдельным альтернативам на значение вероятности и получить на этой основе интегральный показатель уровня риска, соответствующий каждой из альтернатив принятия решений. Сравнение этого интегрального показателя по отдельным альтернативам позволяет избрать для реализации ту из них, которая приводит к избранной цели (заданному показателю эффективности) с наименьшим уровнем риска.
Оценка вероятности реализации отдельных ситуаций развития событий может быть получена экспертным путем.
Исходя из матрицы решений, построенной в условиях риска с учетом вероятности реализации отдельных ситуаций, рассчитывается интегральный уровень риска по каждой из альтернатив принятия решений.
Принятие решений в условиях неопределенности основано на том, что вероятности различных вариантов ситуаций развития событий субъекту, принимающему рисковое решение, неизвестны. В этом случае при выборе альтернативы принимаемого решения субъект руководствуется, с одной стороны, своим рисковым предпочтением, а с другой — соответствующим критерием выбора из всех альтернатив по составленной им «матрице решений».
Основные критерии, используемые в процессе принятия решений в условиях неопределенности, представлены ниже.
1. Критерий Вальда (критерий «максимина»)
2. Критерий «максимакса»
3. Критерий Гурвица (критерий «оптимизма-пессимизма» или «альфа-критерий»)
4. Критерий Сэвиджа (критерий потерь от «минимакса»)
a. Критерий Вальда
Критерий Вальда (или критерий «максимина») предполагает, что из всех возможных вариантов «матрицы решений» выбирается та альтернатива, которая из всех самых неблагоприятных ситуаций развития события (минимизирующих значение эффективности) имеет наибольшее из минимальных значений (т.е. значение эффективности, лучшее из всех худших или максимальное из всех минимальных).
Критерием Вальда (критерием «максимина») руководствуется при выборе рисковых решений в условиях неопределенности, как правило, субъект, не склонный к риску или рассматривающий возможные ситуации как пессимист.
b. Критерий «максимакса»
Критерий «максимакса» предполагает, что из всех возможных вариантов «матрицы решений» выбирается та альтернатива, которая из всех самых благоприятных ситуаций развития событий (максимизирующих значение эффективности) имеет наибольшее из максимальных значений (т.е. значение эффективности лучшее из всех лучших или максимальное из максимальных).
Критерий «максимакса» используют при выборе рисковых решений в условиях неопределенности, как правило, субъекты, склонные к риску, или рассматривающие возможные ситуации как оптимисты.
c. Критерий Гурвица
Критерий Гурвица (критерий «оптимизма-пессимизма» или «альфа-критерий») позволяет руководствоваться при выборе рискового решения в условиях неопределенности некоторым средним результатом эффективности, находящимся в поле между значениями по критериям «максимакса» и «максимина» (поле между этими значениями связано посредством выпуклой линейной функции). Оптимальная альтернатива решения по критерию Гурвица определяется на основе следующей формулы:
А i=а *Э MAXi+ (1 - а) * Э MINi,
где A i — средневзвешенная эффективность по критерию Гурвица для конкретной альтернативы;
а — альфа-коэффициент, принимаемый с учетом рискового предпочтения в поле от 0 до 1 (значения, приближающиеся к нулю, характерны для субъекта, не склонного к риску; значение равное 0,5 характерно для субъекта, нейтрального к риску; значения, приближающиеся к единице, характерны для субъекта, склонного к риску);
Э MAXi — максимальное значение эффективности по конкретной альтернативе;
Э MINi — минимальное значение эффективности по конкретной инициативе.
Критерий Гурвица используют при выборе рисковых решений в условиях неопределенности те субъекты, которые хотят максимально точно идентифицировать степень своих конкретных рисковых предпочтений путем задания значения альфа-коэффициента.
d. Критерий Сэвиджа
Критерий Сэвиджа (критерий потерь от «минимакса») предполагает, что из всех возможных вариантов «матрицы решений» выбирается та альтернатива, которая минимизирует размеры максимальных потерь по каждому из возможных решений. При использовании этого критерия «матрица решения» преобразуется в «матрицу потерь» (один из вариантов «матрицы риска»), в которой вместо значений эффективности проставляются размеры потерь при различных вариантах развития событий.
Критерий Сэвиджа используется при выборе рисковых решений в условиях неопределенности, как правило, субъектами, не склонными к риску.
20 Основные определения теории нечетких множеств
При помощи нечетких множеств можно формально определить неточные и многозначные понятия, такие как «высокая температура», «молодой человек», «средний рост» либо «большой город». Перед формулированием определения нечеткого множества необходимо задать так называемую область рассуждений (universe of discourse). В случае неоднозначного понятия «много денег» большой будет признаваться одна сумма, если мы ограничимся диапазоном [0, 1000 руб] и совсем другая - в диапазоне [0, 1000000 руб]. Область рассуждений, называемая в дальнейшем пространством или множеством, будет чаще всего обозначаться символом 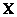 . Необходимо помнить, что
. Необходимо помнить, что 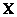 - четкое множество.
- четкое множество.
Нечетким множеством  в некотором (непустом) пространстве
в некотором (непустом) пространстве 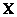 , что обозначается как
, что обозначается как  , называется множество пар
, называется множество пар
 , (1)
, (1)
где
 (2)
(2)
- функция принадлежности нечеткого множества  . Эта функция приписывает каждому элементу
. Эта функция приписывает каждому элементу  степень его принадлежности к нечеткому множеству
степень его принадлежности к нечеткому множеству  , при этом можно выделить три случая:
, при этом можно выделить три случая:
1)  означает полную принадлежность элемента
означает полную принадлежность элемента  к нечеткому множеству
к нечеткому множеству  , т.е.
, т.е.  ;
;
2)  означает отсутствие принадлежности элемента
означает отсутствие принадлежности элемента  к нечеткому множеству
к нечеткому множеству  , т.е.
, т.е.  ;
;
3)  означает частичную принадлежность элемента
означает частичную принадлежность элемента  к нечеткому множеству
к нечеткому множеству  .
.
В литературе применяется символьное описание нечетких множеств. Если 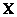 - это пространство с конечным количеством элементов, т.е.
- это пространство с конечным количеством элементов, т.е. 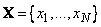 , то нечеткое множество
, то нечеткое множество  записывается в виде
записывается в виде
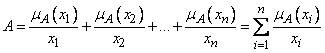 . (3)
. (3)
Приведенная запись имеет символьный характер. Знак «–» не означает деления, а означает приписывание конкретным элементам  степеней принадлежности
степеней принадлежности  . Другими словами, запись
. Другими словами, запись
 ,
,  (4)
(4)
означает пару
 ,
,  . (5)
. (5)
Точно также знак «+» в выражении (3) не означает операцию сложения, а интерпретируется как множественное суммирование элементов (5). Следует отметить, что подобным образом можно записывать и четкие множества. Например, множество школьных оценок можно символически представить как
 , (6)
, (6)
что равнозначно записи
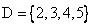 . (7)
. (7)
Если 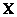 - это пространство с бесконечным количеством элементов, то нечеткое множество
- это пространство с бесконечным количеством элементов, то нечеткое множество  символически записывается в виде
символически записывается в виде
 . (8)
. (8)
Пример 1
Допустим, что  - множество натуральных чисел. Определим понятие множества натуральных чисел, «близких числу 7». Это можно сделать определением следующего нечеткого множества
- множество натуральных чисел. Определим понятие множества натуральных чисел, «близких числу 7». Это можно сделать определением следующего нечеткого множества  :
:
 . (9)
. (9)
Пример 2
Если  , где
, где  - множество действительных чисел, то множество действительных чисел, «близких числу 7», можно определить функцией принадлежности вида
- множество действительных чисел, то множество действительных чисел, «близких числу 7», можно определить функцией принадлежности вида
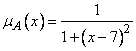 . (10)
. (10)
Поэтому нечеткое множество действительных чисел, «близких числу 7», описывается выражением
 . (11)
. (11)
Замечание 1
Нечеткие множества натуральных или действительных чисел, «близких числу 7», можно записать различными способами. Например, функцию принадлежности (10) можно заменить выражением
 (12)
(12)
На рис. 1а и 1б представлены две функции принадлежности нечеткого множества  действительных чисел, «близких числу 7».
действительных чисел, «близких числу 7».

Рис. 1. Иллюстрация к примеру 2: функции принадлежности нечеткого множества действительных чисел, «близких числу 7».
Пример 3
Формализуем неточное определение «подходящая температура для купания в Балтийском море». Зададим область рассуждений в виде множества  . Отдыхающий I, лучше всего чувствующий себя при температуре 21°, определил бы для себя нечеткое множество
. Отдыхающий I, лучше всего чувствующий себя при температуре 21°, определил бы для себя нечеткое множество
 . (13)
. (13)
Отдыхающий II, предпочитающий температуру 20°, предложил бы другое определение этого множества:
 . (14)
. (14)
С помощью нечетких множеств  и
и  мы формализовали неточное определение понятия «подходящая температура для купания в Балтийском море». В некоторых приложениях используются стандартные формы функций принадлежности. Конкретизируем эти функции и рассмотрим их графические интерпретации.
мы формализовали неточное определение понятия «подходящая температура для купания в Балтийском море». В некоторых приложениях используются стандартные формы функций принадлежности. Конкретизируем эти функции и рассмотрим их графические интерпретации.
1. Функция принадлежности класса  (рис. 2) определяется как
(рис. 2) определяется как
 (15)
(15)
где  . Функция принадлежности, относящаяся к этому классу, имеет графическое представление (рис. 2), напоминающее букву «
. Функция принадлежности, относящаяся к этому классу, имеет графическое представление (рис. 2), напоминающее букву « », причем ее форма зависит от подбора параметров
», причем ее форма зависит от подбора параметров 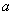 ,
,  и
и  . В точке
. В точке  функция принадлежности класса
функция принадлежности класса  принимает значение, равное 0,5.
принимает значение, равное 0,5.
2. Функция принадлежности класса  (рис. 3) определяется через функцию принадлежности класса
(рис. 3) определяется через функцию принадлежности класса  :
:
 (16)
(16)
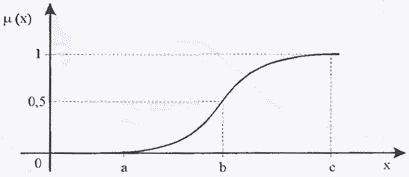
Рис. 2. Функция принадлежности класса  .
.

Рис. 3. Функция принадлежности класса  .
.
Функция принадлежности класса  принимает нулевые значения для
принимает нулевые значения для  и
и  . В точках
. В точках  ее значение равно 0,5.
ее значение равно 0,5.
3. Функция принадлежности класса  (рис. 4) задается выражением
(рис. 4) задается выражением
 (17)
(17)
Читатель с легкостью заметит аналогию между формами функций принадлежности классов  и
и  .
.
4. Функция принадлежности класса  (рис. 5) определяется в виде
(рис. 5) определяется в виде
 (18)
(18)






