4.1 Определение крутящего момента, передаваемого валом
Крутящий момент Мк, возникающий в сечениях вала, определяется /2, с.236/ по формуле::
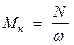. (3)
где N - мощность на валу, Вт;
- угловая скорость вращения вала, рад/с.
Тогда по формуле (3)
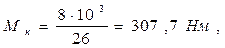
Зная величину Мк и положения крайних сечений скручиваемого участка вала (рисунок 2, а), строится эпюра крутящих моментов (рисунок 2, б).
4.2 Определение окружных усилий в зацеплениях
Окружные усилия Ft1 и Ft2 в зацеплениях (см. рисунок 1) определяются, исходя из условия равновесия вала, то есть
,
тогда
. (4)
4.2.1 Окружное усилие на первом колесе Ft1 определяется из условия (4):
,
.
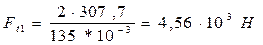4.2.2 Окружное усилие Ft2 на втором колесе определяется из условия (4)
,
.
4.3 Определение радиальных усилий в зацеплениях
Радиальные усилия Fr1 и Fr2 в зацеплениях (см. рисунок 1) определяются по зависимости (1).
Тогда радиальное усилие на первом колесе
.
Радиальное усилие на втором колесе
.
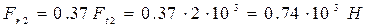4.3.1 Определение осевого усилия на втором колесе
.
4.4 Построение эпюры изгибающих моментов в вертикальной плоскости
4.4.1 Изгиб вала в вертикальной плоскости вызывается радиальными силами Fr1 и Fr2, а также осевой силой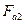 
. Расчетная схема вала для этого случая представлена на рисунке 2, в. Для построения эпюры изгибающих моментов в плоскости хОу необходимо определить составляющие реакции подшипников в этой плоскости YA и YB. Для их определения составляются и решаются уравнения равновесия статики:
,
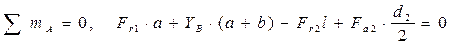откуда
,
,
,
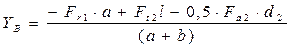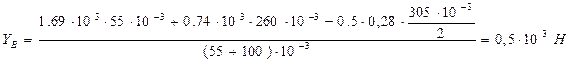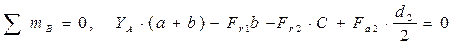откуда
,
C=l-(a+b)=260-(55+100)=105 мм
.
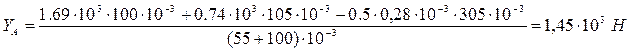4.4.2 Выполняется проверка правильности определения реакций опор. Для этого составляется уравнение равновесия статики в виде суммы проекций всех на ось Оу:
,
,
.
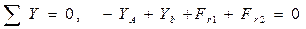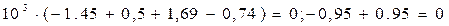Таким образом, реакции опор, определены, верно.
4.4.3 Определяются значения изгибающих моментов в вертикальной плоскости в характерных сечениях А, B, C и D:
.
,
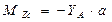или
.
,
.
.
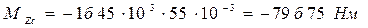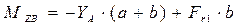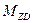
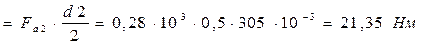Cтроим эпюру Mz (рисунок 2г)
4.5 Построение эпюры изгибающих моментов в горизонтальной плоскости
4.5.1 Изгиб вала в горизонтальной плоскости вызывается силой Ft1 и Ft2. Для удобства построения эпюры изгибающих моментов горизонтальная плоскость xOz совмещается с вертикальной хОу согласно правилам проецирования.
Из уравнений равновесия статики определяются составляющие реакций опор в горизонтальной плоскости (рисунок 2, д):
,
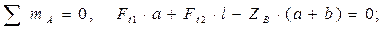отсюда
,
.
,
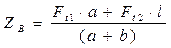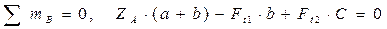тогда
,
.
4.5.2 Для проверки правильности определения реакций составляется уравнение проекций всех сил на ось Оz.
,
,
.
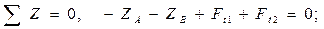Следовательно, реакции ZА и ZВ определены правильно.
 |
4.5.3 Определяются значения изгибающих моментов в характерных сечениях A, B, C и D в горизонтальной плоскости:
.
;
.
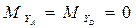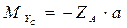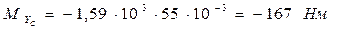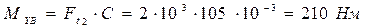
4.6 Построение эпюры результирующих изгибающих моментов
Для построения эпюры результирующих изгибающих моментов (рисунок 2, ж) используется зависимость /3,с. 377/:
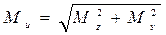, (5)
где Ми - результирующий изгибающий момент в рассматриваемом сечении;
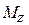- изгибающий момент в том же сечении в вертикальной плоскости;
- изгибающий момент в том же сечении в горизонтальной плоскости
По формуле (5) определяются значения результирующих изгибающих моментов в характерных сечениях А, B, C и D вала:
,
,
.
,
.
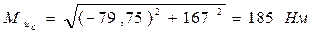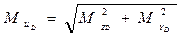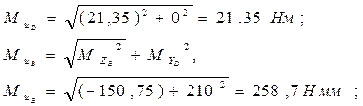По полученным данным строится эпюра результирующих изгибающих моментов (смотри рисунок 2, ж). Из анализа эпюр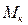 
и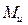 
видно, что опасным сечением вала является сечение B.
4.7 Определение диаметра вала
Диаметр вала определяется по гипотезе максимальных касательных напряжений (2), которая для изгиба с кручением приводится к виду /1, с. 308/:
, (6)
где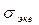 
- эквивалентное напряжение при сложном напряженном состоянии;
М прив - приведенный момент, который по гипотезе наибольших касательных напряжений равен
,
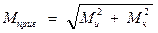где 
.
В опасном сечение B приведенный момент равен
,
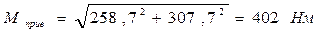W - осевой момент сопротивления сечения. Для круглого поперечного сечения
,
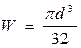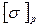- допускаемое напряжение для материала вала при одноосном растяжении, 
.
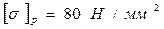На основании условия прочности (6) расчетная формула запишется следующим образом:
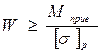. (7)
После подстановки выражения осевого момента сопротивления сечения для круга в неравенство (7) получим расчетную формулу для определения диаметра вала
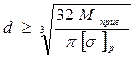. (8)
Для опасного сечения B рассчитываемого вала по формуле (8) определяется диаметр
.
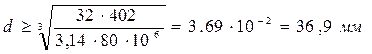Округляя до ближайшего большего значения по стандарту /4/, принимается диаметр вала d=40 мм.
Заключение
В результате расчета промежуточного вала редуктора получено значение диаметра в опасном сечении вала, равное 40 мм, удовлетворяющее условию прочности при изгибе с кручением по гипотезе максимальных касательных напряжений.
Литература
1 Феодосьев В.И. Сопротивление материалов. -М: Высшая школа, 1986. -512с.
2 Писаренко Г.С. и др. Справочник по сопротивлению материалов. -Киев Hayкова думка, 1988. -735с.
3 Беляев Н.М. Сопротивление материалов. -М.: Наука, 1976. -608с.
4 ГОСТ 6636-69. Нормальные линейные размеры.
