Простейшим примером алгоритма является алгоритм линейной структуры. Он применится для вычислительных процессов, в которых операции выполняются в строго определенной последовательности.
Пример. Составить блок-схему вычисления площади S треугольника с заданными сторонами a, b, c.
Алгоритм линейной структуры реализуется следующим образом (рис. 1). Начало процесса обработки данных — блок 1.
Для проведения вычислений осуществляется ввод исходных данных в память ЭВМ – значений длин сторон треугольника a, b, c (блок 2). Перед вычислением величины площади треугольника S (блок 4) необходимо сначала вычислить полупериметр P (блок 3). После вычислений осуществляется вывод результата на печать (блок 5) и остановка (блок 6).

Рисунок 1 - Блок-схема алгоритма линейной структуры
Однако решение абсолютного большинства прикладных задач невозможно свести к алгоритмам линейной структуры. Как правило, вычислительный процесс предусматривает несколько возможных путей решения задач, реализация которых зависит от выполнения некоторых условий. Проверка этих условий осуществляется в логических блоках.
Например, необходимо вычислить значения функции f, которые определяются по одной из трех формул в зависимости от значения х.
Пример. Составить блок-схему для вычисления и вывода значения f для x=1.5 и A=2.8.

|
, если x<-1,
, если 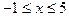 ,
, если x>5. ,
, если x>5.
|
Блок-схема алгоритма решения данной задачи приведена на рис. 2. Для вычисления значения f надо проверить два из трех взаимоисключающих условий (для x<-1 и x>5).
После ввода исходных данных (блок 2) проверяется первое условие x<-1 (блок 3). Если оно выполняется, то значение f определяется по первой ветви формулы (блок 4). В противном случае проверяется любое из условий, которые остались (они взаимоисключающие) — в данном случае в блоке 5 проверяется условие x>5. Если оно выполняется, значение f вычисляется по третьей ветви формулы (блок 6), в противном случае — по второй ветви в блоке 7. В блоке 8 на экран дисплея выводятся значение x и f.
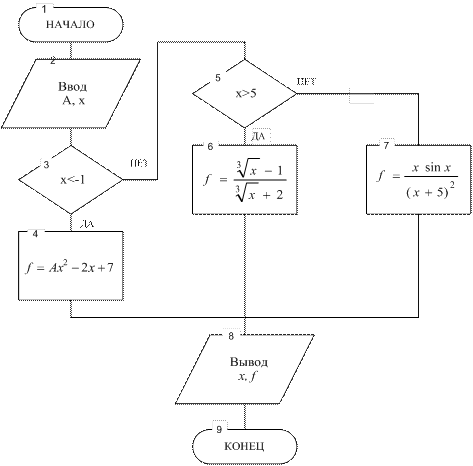
Рисунок 2 - Блок-схема алгоритма с разветвляющейся структурой






