Для анализа работы электрических цепей и улучшения режимов их работы, особенно в схемах электроники, важно знать распределение потенциала в цепи. Графическое изображение распределения потенциала в электрической цепи называется потенциальной диаграммой.
Потенциальная диаграмма строится следующим образом. Потенциал одной точки считают равным нулю, т. е. эту точку заземляют, а потенциалы других точек вычисляются по формулам, например, 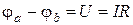 . Затем по оси абсцисс откладывают в масштабе сопротивления в том порядке, в котором они следуют друг за другом при обходе контура цепи, а по оси ординат откладывают в масштабе значения потенциалов точек цепи.
. Затем по оси абсцисс откладывают в масштабе сопротивления в том порядке, в котором они следуют друг за другом при обходе контура цепи, а по оси ординат откладывают в масштабе значения потенциалов точек цепи.
Поясним построение потенциальной диаграммы на примере. Построим потенциальную диаграмму для электрической цепи, схема которой приведена на рисунке 32, если известны следующие значения:

Внутренним сопротивлением источника ЭДС пренебрежем. Если направление обхода контура совпадает с направлением ЭДС (от минуса к плюсу источника), то ЭДС берется со знаком плюс, и со знаком минус – если не совпадает.
Определяем величину тока в цепи:

 |
Рисунок 32 – Схема замещения электрической цепи для
построения потенциальной диаграммы
Начнем обход электрической цепи с точки  , потенциал которой примем равным нулю, т. к. соединен с землей. При переходе от точки
, потенциал которой примем равным нулю, т. к. соединен с землей. При переходе от точки  в точку
в точку  проходим сопротивление
проходим сопротивление  , в котором имеет место падение напряжения
, в котором имеет место падение напряжения  , т. е.
, т. е.  .Тогда потенциал в точке
.Тогда потенциал в точке  будет равен
будет равен  . Между точками
. Между точками  и
и  в цепи включен источник ЭДС, разность потенциалов на его зажимах будет
в цепи включен источник ЭДС, разность потенциалов на его зажимах будет  , откуда
, откуда  . Потенциал точки
. Потенциал точки  ниже потенциала точки
ниже потенциала точки  на величину падения напряжения
на величину падения напряжения  , т. е.
, т. е.  , откуда
, откуда  . Если положительный заряд источника ЭДС присоединен к точке
. Если положительный заряд источника ЭДС присоединен к точке 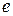 , а отрицательный – к точке
, а отрицательный – к точке  , то
, то  , откуда
, откуда  . Потенциал точки
. Потенциал точки 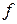 ниже потенциала точки
ниже потенциала точки 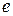 на величину падения напряжения
на величину падения напряжения  , т. е.
, т. е.  , откуда
, откуда  . Потенциал точки
. Потенциал точки  выше потенциала точки
выше потенциала точки 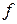 на величину ЭДС
на величину ЭДС  , т. е.
, т. е.  , откуда
, откуда  . Находим потенциал точки
. Находим потенциал точки  как
как 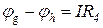 , откуда
, откуда  и конечная точка
и конечная точка 
 , откуда
, откуда  . По результатам полученных вычислений строим потенциальную диаграмму (рисунок 33).
. По результатам полученных вычислений строим потенциальную диаграмму (рисунок 33).






