Для указанных в физической модели условий можно принять показатель адиабаты для газа k=1,4, газовая постоянная R=287,13 Дж/K·кг, атмосферное давление pатм=101325 Па, плотность воздуха ρ=1,225 кг/м3.
Уравнение закона обращенного воздействия для данной модели
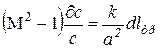(1)
Уравнение неразрывности:
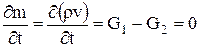, (2)
Подставив в (1) уравнения (3)
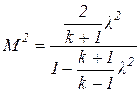
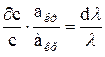и 
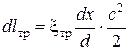, (3)
получается дифференциальное уравнение приведенной скорости в произвольном сечении трубы.
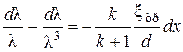, (4)
где dx –элемент длины трубы, на котором коэффициент сопротивления трения постоянен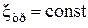 
.
Если принять 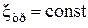вдоль трубы и проинтегрировать, получим
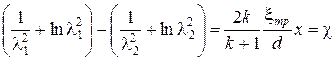, (5)
где χ – приведенная длина трубы – характеризует особенности газа и течения,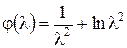 
- газодинамическая функция.
Сокращенно уравнение (5) примет вид
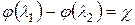(6)
Определение критической приведенной длины трубы
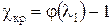. (7)
Уравнение расхода в газодинамической форме:
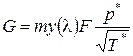, (8)
где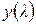 
- газодинамическая функция, m - постоянный коэффициент рода газа:
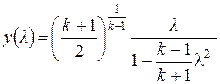(9)
.
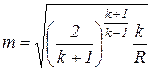Максимальное значение расхода газа
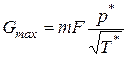. (10)
Для расчета параметров перед скачком пользуются газодинамическими функциями основных параметров газового потока:
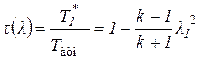, (11)
(12)
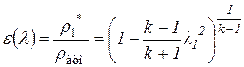(13)
Расчет скорости и параметров после скачка:
,
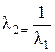
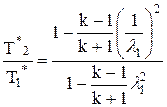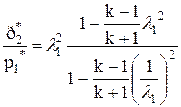(14)
