Под энергией ионной кристаллической решетки понимают работу, которую при постоянной температуре и давлении необходимо совершить, чтобы разрушить 1 моль ионного кристалла с образованием газообразных ионов, бесконечно удаленных друг от друга (в состоянии "ионного газа"). В приведенных условиях работа равна изменению энергии Гиббса в процессе превращения кристалла в ионный газ. Традиционно энергия ионной кристаллической решетки обозначается символом U.
U = DG (1.1)
Энергия кристаллической решетки при абсолютном нуле (0 К) может быть вычислена с помощью теории М. Борна. В основе теории лежит предположение, что энергия ионного кристалла складывается из энергии электростатического взаимодействия ионов в соответствии с законом Кулона и обменной энергии отталкивания этих ионов, изменяющейся обратно пропорционально n-ой степени расстояния между ними. При 0 К каждый ион занимает определенное положение в кристалле, соответствующее минимуму его энергии. Следовательно, для того чтобы вычислить величину энергии ионной кристаллической решетки, достаточно просуммировать энергии всех указанных выше взаимодействий, считая положение каждого иона заданным. Покажем, как можно осуществить такое суммирование для кулоновского взаимодействия. Для этого рассмотрим модель ионного кристалла в виде цепочки знакочередующихся ионов, имеющих одинаковый по модулю заряд ÷Ze÷ и расположенных друг от друга на расстоянии r0, как это показано на рис.1.1.
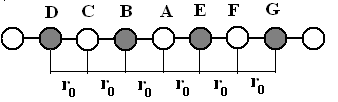
Рис.1.1. Схематическое изображение ионов в кристаллической решётке
Анион A в данном случае испытывает кулоновское притяжение двух непосредственных соседей: катионов В и Е, потенциальная энергия взаимодействия с которыми, выраженная в системе СИ, равна:
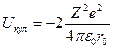
Одновременно ион А отталкивается от находящихся на расстоянии 2r0 от него одноименных с ним анионов C и F; энергия этого взаимодействия записывается:
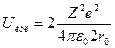
(энергия притяжения принимается отрицательной, а энергия отталкивания – положительной)
Общая кулоновская энергия взаимодействия иона А со всеми ионами цепочки может быть представлена в виде:
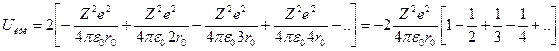(1.2)
Характерной особенностью выражения (1.2) является то, чтоего можно представить ввиде произведения энергии:
взаимодействия двух ионов, находящихся на равновесном расстоянии друг от друга - r0, на величину, определяемую только структурой рассматриваемой нами системы и не зависящей ни от зарядов ионов, ни от расстояния между ними:
Сумма ряда, заключенного в скобках, равна ln2, поэтому можно записать, что
(1.3)
Буквой М впоследнем выражении обозначена т.н. константа Маделунга, получившая название по имени ученого, вычислившего её значения для основных типов кристаллов. Константа Маделунга отражает расположение ионов в пространстве и определяется только типом рассматриваемой кристаллической структуры.
Обобщая рассмотренный пример на случай трехмерных ионных кристаллов, состоящих из ионов одинакового заряда, заметим, что полную энергию кулоновского взаимодействия одного иона с остальной частью кристалла всегда можно записать в виде произведения энергии взаимодействия элементарных структурных единиц (ионов) и геометрического фактора (константы Маделунга). Так, для кристаллов каменной соли NaCl, где каждый ион впространстве окружен 6 ионами противоположного заряда (координационное число равно 6), расположенными на расстоянии r0и 12 ионами содинаковым зарядом на расстоянии r0Ö2, расчет приводит кМ = 1,7476. В настоящее время разработаны математические методики расчетов М для решеток разных типов. Для некоторых из них величины М приведены в табл.1.1. Более подробные таблицы значений М приведены в справочниках.
Если пренебречь возможными искажениями реальной структуры кристалла, влиянием поверхностных эффектов на его свойства и считать, что все ионы кристалла находятся в одинаковом окружении, то можно найти полную электростатическую энергию 1 моля кристалла. Как известно, 1 моль ионного кристалла содержит Naположительно заряженных и Na отрицательно заряженных ионов (Na - число Авогадро). Для каждого из этих ионов энергия взаимодействия с решеткой кристалла передается выражением (1.3), поэтому кулоновскую энергию ионного кристалла можно записать в следующем виде:
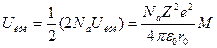(1.4)
Множитель 1/2 в выражении появился в связи с тем, что каждую пару ионов при подсчете энергии мы должны учитывать только один раз.
Таблица 1.1
Константы Маделунга некоторых кристаллических решёток
| Тип решетки | Пример | M | Координационное число |
| Хлорид цезия Каменная соль Сфалерит Вюрцит | CsCl NaCl ZnS ZnS | 1,7627 1,7476 1,6381 1,6413 | Cs- 8; CI - 8 Na– 6; CI –6 Zn - 4 S-4; Zn – 4, S - 4 |
Выражение (1.4) может быть обобщено и на случай ионных кристаллов, составленных из ионов, имеющих различные заряды:
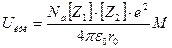(1.5 )
где через Z1 и Z2 обозначены заряды катиона и аниона. Константа Маделунга в этом случае, однако, не имеет простого геометрического смысла.
Как указывалось выше, согласно теории М. Борна, при расчетах анергии кристалла следует принять во внимание и энергию обменного отталкивания, возникающую из-за перекрывания электронных орбиталей ионов при их сближении. Для двух взаимодействующих ионов эта энергия может быть записана следующим образом:
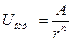, (1.6)
где А - константа энергии отталкивания, r - расстояние между нонами, а n - постоянная, характеризующая зависимость энергии обменного отталкивания ионов от расстояния между ними. Рассматривая энергию обменного отталкивания ионов в кристалле, мы, как и раньше, должны были бы провести её суммирование по всем парам взаимодействующих ионов, а затем сложить с энергией кулоновского взаимодействия. Однако можно поступить иначе. Предположим, что нам удалось вычислить сумму энергий отталкивания (1.6) и представить её в виде произведения величин, определяемых законом взаимодействия двух ионов и геометрией кристалла:
(1.7)
В соответствии с определением М.Борна, полную энергию ионного кристалла можно представить как сумму Uкул и Uотт, взятую с обратным знаком:
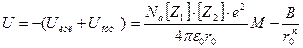(1.8)
Так как r0, представляет собой равновесное расстояние между ионами в кристалле, то оно должно отвечать условию минимума энергии решетки:
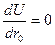(1.9)
Продифференцировав (1.8) по r0и приравняв полученную производную нулю, получаем уравнение
(1.10)
из которого можно определить величину:
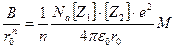(1.11)
Подставляя последнее выражение в (1.8), получаем формулу Борна для энергии кристаллической решетки:
(1.12)
Величину nобычно находят из данных по изотермической сжимаемости ионных кристаллов. Для решеток галогенидов щелочных металлов значения nприведены в табл.1.2.
Таким обрезом, в теории Борна рассматривается статическая решетка ионного кристалла, поэтому энергия ионной кристаллической решетки, вычисляемая с помощью выражения (1.12), не включает в себя энергию теплового и, в частности, колебательного движения ионов. С физической точки зрения именно это означает, что энергия, вычисляемая с помощью теории Борна, относится к абсолютному нулю температуры (0 К). Согласно тепловой теореме Нернста
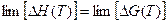
поэтому при нуле Кельвина энергия ионной кристаллической решетки будет совпадать со значением теплового эффекта её разрушения:
U = DG0 = DH0 (1.13)
Таблица 1.2
Значения параметра n галогенидов щелочных металлов
| F | Cl | Br | I | |
| Li | 5,86 | 6,66 | 7,00 | 6,15 |
| Na | 8,00 | 8,16 | 8,02 | 7,98 |
| K | 8,05 | 8,87 | 9,08 | 9,29 |
| Rb | 8,80 | 8,12 | 8,72 | 9,49 |
| Cs | 13,0 | 13,1 | 13,2 | 12,7 |
Величины DGT и DНТпри температуре Т, отличной от нуля, будут различаться между собой на T×DST.
Величину энергии, рассчитываемой по уравнению Борна U = DH0, можно определить другим способом, например, из т.н. цикла Борна - Габера. Кристалл галогенида щелочного металла можно синтезировать двумя разными путями: непосредственно из простых веществ (I) и путем их последовательных превращений (П):
Цикл замкнут, поэтому согласно закону Гесса, суммарное изменение энтальпии åDНi = 0:
DН1 + DН2 + DН3 + DН4 + DHX - DH5 = 0 (1.14)
Стандартные значения изменений энтальпии для процессов 1 - 5 можно найти из справочника, а из уравнения (1.14) вычислить величину DНХ, которая равна изменению энтальпии образования кристалла, взятому с обратным знаком - DНХ = DНреш.
Рассмотрим подробно расчет теплового эффекта разрушения кристаллической решетки NaCl при T =298К.
1) Na(крист) Þ Na(газ) DН1 = 108,8 кДж/моль
2) Na(газ) Þ Na+(газ) DН2 = 496,9 кДж/моль
3) 1/2Cl2(газ) Þ Cl (газ) DН3 = 121,6 кДж/моль
4) Cl(газ) Þ Cl-(газ) DН4 = -365,8 кДж/моль
5) Na(крист) + 1/2Cl2(газ) Þ NaCl(крист) DН5 = -411,5 кДж/моль
С учётом выражения (1.14) получаем -DНХ = 108,8 + 496,9 + 121,6 – 365,8 + 411,5 = 773,0 кДж/моль
Таким образом, в результате рассмотрения цикла Борна – Габера можно определить тепловой эффект разрушения кристаллической решетки DНреш при любой температуре Т. Как уже отмечалось выше, величина этого эффекта при 0 К равна энергии ионной кристаллической решетки U, вычисленной в рамках теории Борна.
Поэтому для сравнения значений энергии кристаллической решеткиU, полученной по формуле Борна и из цикла Борна - Габера, необходимо величину теплового эффекта разрушения ионного кристалла при 298К (DНреш) пересчитать на нуль Кельвина. Такой пересчет можно произвести спомощью уравнения Кирхгоффа, рассматривая процесс разрушения ионного кристалла как квазихимическую реакцию:
NaCl Þ Na+(газ) + Cl-(газ) (I.I5)
DН0 = DНреш(298) +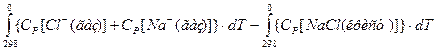 
(I.I6)
Первый интеграл легко вычисляется, если принять ионный газ за идеальный одноатомный газ, мольная теплоемкость Ср которого равна 5/2R. Для вычисления второго интеграла необходимо провести графическое интегрирование от 10 К до 298 К с использованием имеющихся в справочниках табличных значений теплоёмкости Ср[NaCl(крист)]. Вычисления интеграла выполняют на компьютере численным методом с использованием прикладных математических программ «MathCad Professinal 2000» и «Mathematica 5».
Подставив в уравнение (1.16) значения интегралов ивеличину DНреш (298К), рассчитанную из цикла Борна - Габера, получим DН0 = U.
