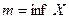Пусть X – числовое множество.
Определение 17.1.
А). Множество X ограниченно снизу тогда и только тогда, когда
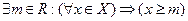 .
.
В). Множество X ограниченно сверху тогда и только тогда, когда 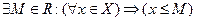 .
.
С). Множество X ограниченно тогда и только тогда, когда X ограниченно сверху и снизу:
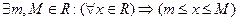 т.е.
т.е. 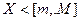 .
.
Очевидно, что любое ограниченное сверху (снизу) множество имеет бесконечно много верхних (нижних граней).
Естественно возникает вопрос о существовании наименьшей из верхних граней ограниченного сверху множества и наибольшей из нижних граней ограниченного снизу множества.
Определение 17.2.
А). Число M называется точной верхней гранью, если оно является наименьшим из всех верхних граней.
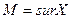
Б). Число m называется точной нижней гранью, если оно является наибольшим из всех нижних граней.