Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж.Био (1774-1862) и Ф.Саваром (1791-1841). Результаты этих опытов было обобщены выдающимся французским математиком и физиком П.Лапласом.
Закон Био-Савара-Лапласа для проводника с током I, элемент длины которого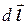 
создает в некоторой точке А индукцию поля 
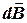записывается в виде
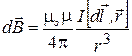. (2.1.)
Направление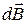 
перпендикулярно 
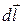и 
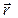, т.е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Поскольку направление 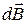можно определить по правилу правого винта, то для модуля dB запишем формулу
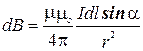, (2.2)
где a - угол между векторам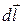и и .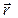
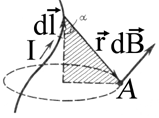
Рис.4. К закону Био-Савара-Лапласа.
Для магнитного поля, также как и для электрического справедлив принцип суперпозиции: если имеется несколько элементов тока или несколько контуров с током, каждый из которых создает магнитное поле, то при одновременном действии всех токов индукция результирующего поля равна векторной сумме отдельных полей: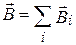 
или в случае элементарных токов
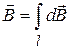, (2.3)
где 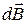магнитная индукция поля, создаваемого элементом интегрирования длиной 
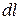. Интегрирование производится по всей длине проводника 
.
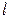Расчет характеристик магнитного поля (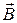
и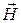 
) по формулам (2.1-2.2) в общем случае сложен. Однако, если распределение тока имеет определенную симметрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет рассчитать конкретные примеры.
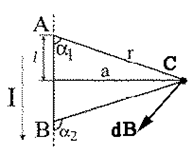1. Магнитное поле отрезка прямого провода с током. Вычислим индукцию магнитного поля, создаваемого отрезком АВ прямолинейного проводника с током I, в точке С, расположенной на перпендикуляре к середине этого отрезка на расстоянии а (рис.5). Индукция магнитного поля в точке С будет равна
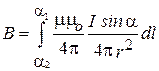. (2.4)
Рис.5.
Но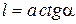 
, тогда 
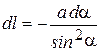и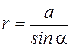 
. Подставив эти значения в (2.4), получим
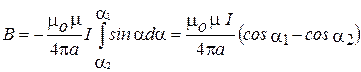(2.5)
2. Магнитное поле бесконечно длинного прямого провода с током. Для такого провода угол a1 = 0, а угол a2 = 180о. Тогда
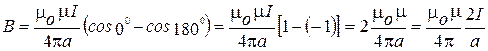, (2.6)
где a – длина перпендикуляра, опущенного из точки наблюдения С на проводник с током.
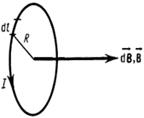3. Магнитное поле в центре кругового проводника с током (рис.6). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления – вдоль нормали от витка. Поэтому сложение векторов 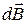можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina = 1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, по закону Био- Савара-Лапласа,
Рис.6. 
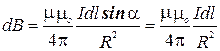
Тогда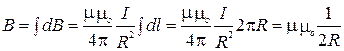 
Следовательно, магнитная индукция поля в центре кругового проводника с током равна
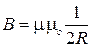. (2.7)
4. Определить индукцию магнитного поля на оси кругового тока радиусом R, в точке А на расстоянии а от плоскости контура, по которому течет ток силой I (рис.7).
Воспользуемся законом Био-Савара-Лапласа
,
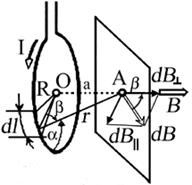
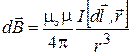где 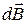магнитная индукция, создаваемая элементом тока 
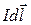в точке, определяемой радиусом-вектором 
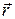. Выделим на кольце элемент 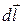и от него в точку А проведем радиус-вектор 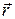. Направление вектора 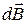определим по правилу правого винта. Согласно принципу суперпозиции, магнитная индукция 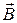в точке А определяется интегрированием 
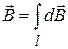, где интегрирование ведется по всем элементам Рис.7. 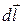кольца. Разложим вектор 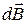на две составляющие: 
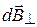перпендикулярную плоскости кольца и 
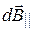, параллельную плоскости кольца, т.е. 
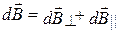. Тогда 
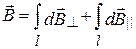. Заметим, что 
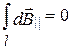из соображений симметрии и что векторы 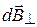от различных элементов 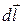сонаправлены. Поэтому заменим векторное суммирование (интегрирование) скалярным 
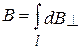, где 
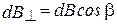и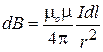 
, поскольку 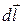перпендикулярен 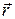и, следовательно, sina =1 (r 2 =R2 + a2).
Таким образом,
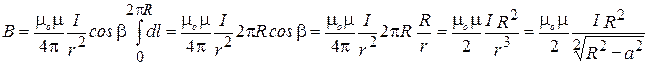Или, окончательно,
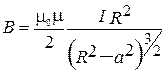. (2.8)
