Для успешного решения задач типа В1 необходимо:
- Уметь выполнять действия с функциями
- Определять значение функции по значению аргумента при различных
способах задания функции; описывать по графику поведение и
свойства функций, находить по графику функции наибольшие и
наименьшие значения; строить графики изученных функций - Вычислять производные и первообразные элементарных функций
Исследовать в простейших случаях функции на монотонность,
находить наибольшие и наименьшие значения функций - Повторить материал по темам:
- Производная
- Понятие о производной функции, геометрический смысл производной
- Физический смысл производной, нахождение скорости для процесса, заданного формулой или графиком
- Уравнение касательной к графику функции
- Производные суммы, разности, произведения, частного
- Производные основных элементарных функций
- Вторая производная и ее физический смысл
- Исследование функций
- Применение производной к исследованию функций и построению
графиков - Примеры использования производной для нахождения наилучшего
решения в прикладных, в том числе социально-экономических задачах мостоятельного решения:
. 
Ответ: 4
2. На рисунке изображен график производной функции f(x),
определенной на интервале (—7; 5). Найдите точку
экстремума функции f(x), принадлежащих отрезку [—6; 4].
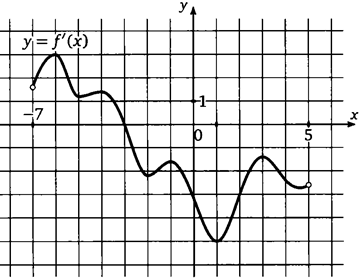
Ответ: -3
3. На рисунке изображен график производной функции f(x),
определенной на интервале (—3; 8). Найдите количество
точек максимума функцииf(x), принадлежащих отрезку [—2; 7].

Ответ: 2
4. На рисунке изображен график функции у =f(x) и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции f(x) в точке х0.

Ответ: 3
5. На рисунке изображен график функции у = f(x) и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции f(x) в точке х0.

Ответ: 0.5
6. На рисунке изображен график функции у=f(x) и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции f(x) в точке х0.

Ответ: -3
7. На рисунке изображен график функции у = f(x) и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции f(x) в точке х0.

Ответ: -0.25
8. На рисунке изображен график функции f(x). Касательная к
этому графику, проведенная в точке 4, проходит через начало
координат. Найдите f /(4).

Ответ: 1.5
9. На рисунке изображен график функции у =f(x),
определенной на интервале (-8; 3). Определите количество целых
чисел x таких, что f /(х) отрицательно.
 х=-7;-6;-2,-1.
х=-7;-6;-2,-1.
Ответ: 4
10. На рисунке изображен график функции у = f(x),
определенной на интервале (-8;3). Найдите количество точек, в
которых производная функции f(x) равна 0.

Ответ: 5
11. На рисунке изображен график функции у =f(x),
определенной на интервале (—8;3). Найдите количество точек, в
которых касательная к графику функции параллельна прямой
У = 18.

Ответ: 5
12. На рисунке изображен график производной функции f(x),
определенной на интервале (-3; 8). Найдите промежутки
убывания функции f(x). В ответе укажите сумму целых
чисел, входящих в эти промежутки.

Ответ: 16
13. На рисунке изображен график производной функции f(x),
определенной на интервале (—11; 3). Найдите количество
таких чисел x что касательная к графику функции f(x) в точке
x, параллельна прямой у = Зх — 11 или совпадает с ней.

Ответ: 6
14. На рисунке изображен график производной функции f(x),
определенной на интервале (-11; 3). Найдите промежутки
возрастания функции f(x). В ответе укажите длину
наибольшего из них.

Ответ: 6
15. На рисунке изображен график производной функции f(x),
определенной на интервале (-5; 3). Найдите абсциссу точки,
в которой касательная к графику функции f(x) параллельна
прямой у = 2х + 7 или совпадает с ней.

Ответ: -1
16. Прямая у = 4х + 13 параллельна касательной к графику
функции у = х2 - Зх + 5. Найдите абсциссу точки касания.
Ответ: 3.5
17. Прямая у = 2х + 37 является касательной к графику
функции у = x3 + Зx2 — 7x +10. Найдите абсциссу точки касания.
Ответ: -3
18. Прямая у = Зх + 1 является касательной к графику
функции у = ах2 + 2х + 3. Найдите а.
Ответ: 0.125




