Связный (Если каждую вершину графа можно соединить с любой другой его вершиной некоторой цепью, то граф называется связным.) граф G называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро; такая цепь называется эйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз. Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым; при этом каждый эйлеров граф будет полуэйлеровым.
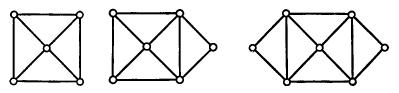
Рис 4.1 Рис. 4.2 Рис 4.3
при этом каждый эйлеров граф будет полуэйлеровым. На рис. 4.1, 4.2 и 4.3 изображены соответственно не эйлеров, полуэйлеров и эйлеров графы. Заметим, что предположение о связности графа G введено только ради удобства, так как оно позволяет не рассматривать тривиальный случай графа, содержащего несколько изолированных вершин.
Лемма. Если степень каждой вершины графа G не меньше двух, то G содержит цикл.
Доказательство. Если в графе G имеются петли или кратные ребра, то утверждение очевидно; поэтому предположим, что G является простым графом. Пусть v — произвольная вершина графа G; построим по индукции маршрут v → v1→ v2..., выбирая вершину v1 смежной вершине v, а для i ≥1 — выбирая v i+1 смежной v i и отличной от
v i-1 (существование такой вершины v i+1 гарантировано условием леммы). Так как G имеет конечное число вершин, то в конце концов мы придем к вершине, которая уже была выбрана раньше. Предположим, что vk — первая такая вершина; тогда часть маршрута, лежащая между двумя вхождениями vk, и является требуемым циклом.
Теорема. Связный граф G является эйлеровым тогда и только тогда, когда каждая вершина в G имеет четную степень.
Доказательство. => Предположим, что Р является эйлеровой цепью в графе G. Тогда при всяком прохождении цепи Р через любую из вершин графа степень этой вершины увеличивается на два. А так как каждое ребро встречается в Р ровно один раз, то каждая вершина должна иметь четную степень.
<= Проведем доказательство индукцией по числу ребер в G. В силу связности G, степень каждой вершины не меньше двух, а отсюда, по предыдущей лемме, заключаем, что граф G содержит цикл С. Если С проходит через каждое ребро графа G, то доказательство завершено; если нет, то, удаляя из G ребра, принадлежащие циклу С, получим новый (быть может, и несвязный) граф Н. Число ребер в Н меньше, чем в G, и любая вершина в Н по-прежнему имеет четную степень Согласно индуктивному предположению, в каждой компоненте графа Н существует эйлерова цепь. В силу связности графа G, каждая компонента в Н имеет по крайней мере одну общую вершину с циклом С, поэтому искомую эйлерову цепь графа G можно получить так: идем по ребрам цикла С до тех пор, пока не встретим неизолированную вершину графа Н, затем следуем по эйлеровой цепи той компоненты в Н, которая содержит указанную вершину; далее продолжаем путь по ребрам цикла С, пока не встретим вершину, принадлежащую другой компоненте графа Н, и т. д.; заканчивается процесс тогда, когда мы попадаем обратно в начальную вершину (см. рис. 4.4).

Рис. 4.4
Модифицируя данное доказательство, легко получить следующие два следствия:
Следствие 1. Связный граф является эйлеровым тогда и только тогда, когда семейство его ребер можно разбить на непересекающиеся циклы.
Следствие 2. Связный граф является полуэйлеровым тогда и только тогда, когда в нем не более двух вершин имеют нечетные степени.
Заметим, что если полуэйлеров граф содержит ровно две вершины с нечетными степенями, то в любой полуэйлеровой цепи (смысл этого понятия очевиден) одна из этих вершин обязательно будет начальной, а другая — конечной. По лемме о рукопожатиях граф не может иметь только одну вершину нечетной степени.
Теорема (алгоритма Флёри). Пусть G — эйлеров граф; тогда следующая процедура всегда возможна и приводит к эйлеровой цепи графа G. Выходя из произвольной вершины и, идем по ребрам графа произвольным образом, соблюдая лишь следующие правила:
(1) стираем ребра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются;
(2) на каждом этапе идем по мосту только тогда, когда нет других возможностей.
Доказательство. Покажем сначала, что указанная процедура может быть выполнена на каждом этапе. Предположим, что мы достигли некоторой вершины v; тогда если v ≠ u, то оставшийся подграф Н связен и содержит ровно две вершины нечетной степени, а именно u и v. Согласно следствию 2, граф Н содержит полуэйлерову цепь Р из v в u. Поскольку удаление первого ребра цепи Р не нарушает связности графа Н, отсюда следует, что описанное в теореме построение возможно на каждом этапе. Если же v = u, то доказательство остается тем же самым до тех пор, пока есть еще ребра, инцидентные вершине u.
Осталось только показать, что данная процедура всегда приводит к полной эйлеровой цепи. Но это очевидно, так как в G не может быть ребер, оставшихся непройденными после использования последнего ребра, инцидентного и (в противном случае удаление некоторого ребра, смежного одному из оставшихся, привело бы к несвязному графу, что противоречит (2)).




