Задачи:
1. Существует ли эйлеров цикл в графе G. Если существует, найдите его.[2]
Решение:
А) Так как каждая вершина имеет чётную степень, то по критерию в этом графе существует эйлеров цикл: 1,4,6,9,10,8,5,3,2,4,7,10,11,8,6,5,2,1
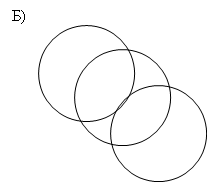
Б) В этом графе также каждая вершина имеет чётную степень, значит, существует и эйлеров цикл: 1,2,3,4,5,3,1,4,5,2,1
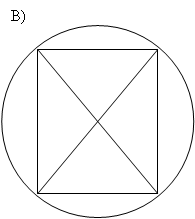
В) Здесь каждая вершина имеет степень 5, то есть нечётную, следовательно, в этом графе (по критерию) нет эйлерова цикла.
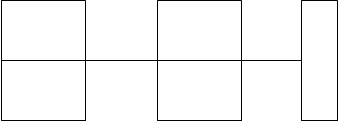
2. Где на выставке следовало бы сделать вход и выход (рис.8), чтобы можно было провести экскурсию по всем залам, побывав в каждом из них в точности один раз?[2]
Решение:
В этом графе вершины А и В имеют степень 3, то есть нечётную, следовательно, в нём существует эйлеров путь с началом в одной из этих вершин и концом в другой. Значит, вход и выход следует установить в вершинах А и В.
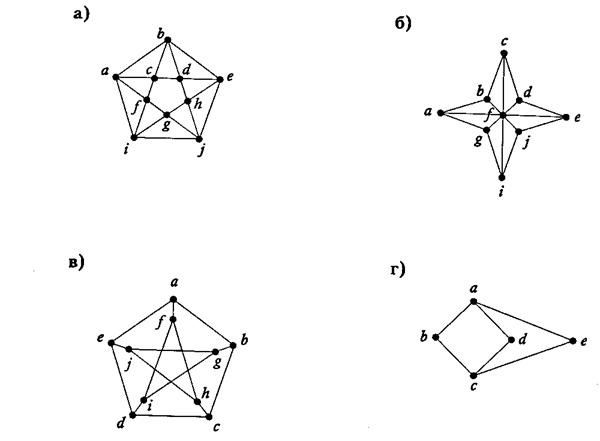
3. Среди приведённых ниже графов найдите те, которые имеют эйлеров цикл.[1]
Решение:
а) Т.к. этот граф связный и каждая его вершина имеет чётную степень, то по критерию эйлерова графа, данный граф имеет эйлеров цикл:
a b e j i f c b d h j g f a c d e h g i a
б) Этот граф связный, но т.к. все его вершины имеют нечётную степень, то он не имеет эйлерова цикла.
в) Этот граф связный, но т.к. все его вершины имеют степень 3, то есть нечётную, то он не имеет эйлерова цикла.
г) Данный граф связный, степени вершин а и с имеют нечётную степень, значит, этот граф не имеет эйлерова цикла.
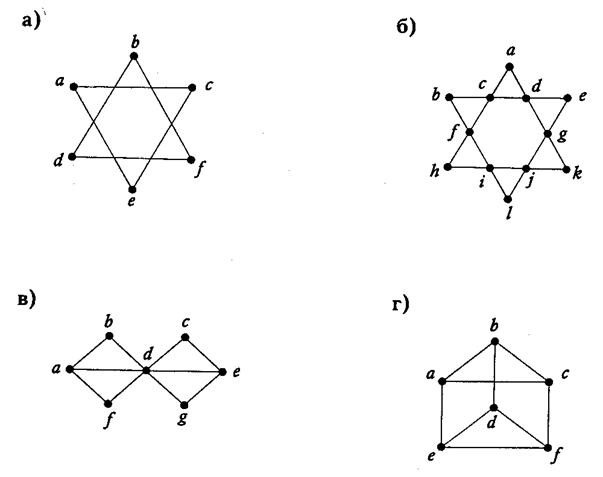
4. Среди приведённых ниже графов найдите те, которые имеют эйлеров цикл.[1]
Решение:
а) Граф не является связным, то есть не выполняется первое условие критерия, значит, он не имеет эйлерова цикла.
б) Этот граф является связным и все его вершины имеют чётную степень, значит, по критерию эйлерова графа, он имеет эйлеров цикл:
a c f h I j k g d c b f I l j g e d a
в) Данный граф связный, но степени вершин а и е нечётные, следовательно по критерию, этот граф не имеет эйлерова цикла.
г) Граф является связным, но так как все его вершины имеют нечётную степень, то граф не имеет эйлерова цикла.
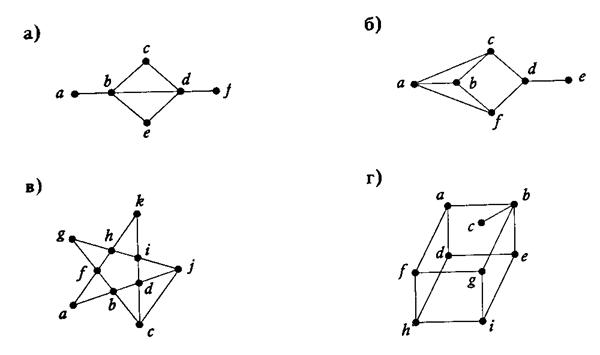
5. Среди приведённых ниже графов найдите те, которые имеют собственный эйлеров путь.[1]
Решение:
а) Граф связный, и только две его вершины (a и f) имеют нечётную степень, следовательно, то по теореме 3, граф имеет собственный эйлеров путь.
б) Граф связный; deg(a)=3, deg(b)=3, deg(c)=3, то есть более двух вершин имеют нечётную степень, значит, не имеет эйлерова пути.
в) Этот граф связный и только две вершины (с и j) имеют нечётную степень, значит, граф имеет собственный эйлеров путь.
г) Граф связный; deg(a)=3, deg(b)=4, deg(c)=1, deg(d)=3, то есть более двух вершин имеют нечётную степень, следовательно, в этом графе нет эйлерова пути.
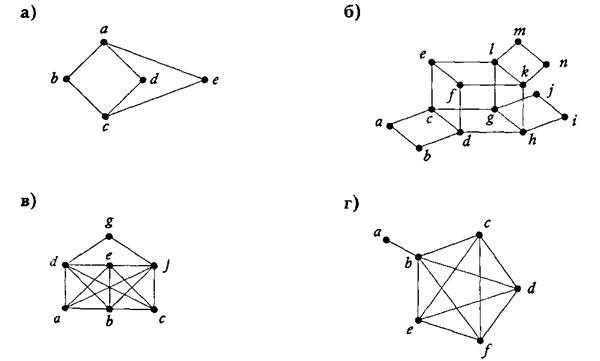
6. Среди приведённых ниже графов найдите те, которые имеют собственный эйлеров цикл.[1]
Решение:
а) Данный граф связный; deg(a)=3, deg(b)=2, deg(c)=3, deg(d)=2, deg(e)=2. Ровно две вершины имеют нечётную степень, значит, по теореме 3, граф имеет собственный эйлеров путь.
б) Граф является связным и ровно две его вершины (е и f) имеют нечётную степень, значит, данный граф имеет собственный эйлеров путь.
в) Граф связный, найдём степени вершин: deg(d)=5, deg(b)=5, deg(e)=5, нашлись три вершины, степень которых нечётная, значит, граф не имеет эйлерова пути.
г) Данный граф связный и только две его вершины (а и b) имеют нечётную степень, значит, этот граф имеет собственный эйлеров путь.
7. Какие из следующих ориентированных графов имеют эйлеровы циклы? [1]
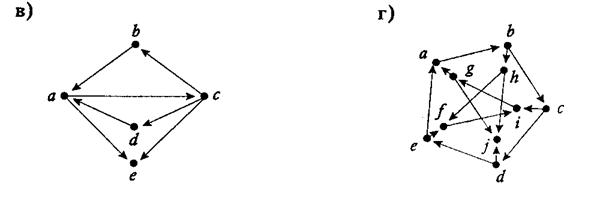Решение:
а) Граф связный, найдём степени входа и выхода вершин (по теореме 5 степени входа и выхода каждой вершины должны совпадать):
indeg(a)=2, outdeg(a)=1, то есть нашлась вершина, у которой не совпадают степени входа и выхода, значит, граф не имеет эйлерова цикла.
б) Граф связный, найдём степени вершин:
indeg(a)=2 outdeg(a)=2
indeg(b)=2 outdeg(b)=2
indeg(c)=2 outdeg(c)=2
indeg(d)=2 outdeg(d)=2
indeg(e)=2 outdeg(e)=2
Следовательно, по теореме 5, граф имеет эйлеров цикл.
в) Граф связный, найдём степени вершин:
indeg(a)=2 outdeg(a)=2
indeg(b)=1 outdeg(b)=1
indeg(c)=3 outdeg(c)=1
Условия теоремы 5 не выполняются, значит, граф не имеет эйлерова цикла.
г)) Граф связный, найдём степени вершин:
indeg(a)=2 outdeg(a)=1
Следовательно, т.к. условия теоремы 5 не выполняются то, граф не имеет эйлерова цикла.
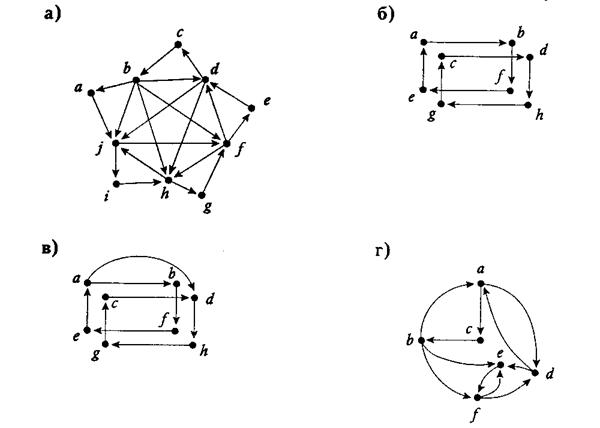
8. Какие из следующих ориентированных графов имеют эйлеровы циклы? [1]
Р
Решение:
а) Граф связный, найдём степени вершин:
indeg(a)=1 outdeg(a)=1
indeg(b)=5 outdeg(b)=1
Т.к. второе условие теоремы 5 не выполняется, значит, граф не имеет эйлерова цикла.
б) Граф не связный, то есть первое условие теоремы 5 не выполняется. Значит, граф не имеет эйлерова цикла.
в) Граф связный, найдём степени вершин:
indeg(a)=2 outdeg(a)=1
Второе условие теоремы 5 не выполняется, значит, граф не имеет эйлерова цикла.
г) Граф связный, найдём степени вершин:
indeg(a)=2 outdeg(a)=2
indeg(b)=3 outdeg(b)=1
Граф не имеет эйлерова цикла, т.к. не выполняется второе условие теоремы 5.
9. На рисунке план подземелья, в одной из комнат которого скрыты богатства рыцаря. После смерти рыцаря его наследники нашли завещание, в котором было сказано, что для отыскания сокровищ достаточно войти в одну из крайних комнат подземелья, пройти через все двери, причём в точности по одному разу через каждую; сокровища скрыты за той дверью, которая будет пройдена последней. В какой комнате были скрыты сокровища?
   1
| |||||
       3
| |||||
| 7
| |||||
        11
| |||||
  16
| |||||
| 20
| |||||
Построим граф, вершинами которого являются комнаты подземелья, а рёбрами – двери. Затем найдём такой путь, чтобы пройти по всем рёбрам (через все двери) в точности по одному разу.
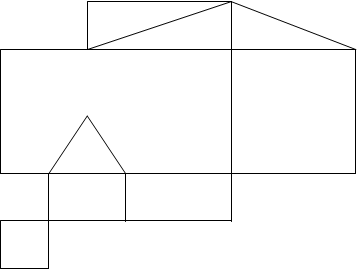
Данный граф имеет эйлеров путь, так как только две вершины имеют нечётную степень, это вершины 6 и 18. Значит, вход и выход могут быть только в вершинах 6 и 18.
Так как комната 6 является крайней, то в ней будет вход, значит, последней комнатой будет 18-ая, следовательно сокровища скрыты в этой комнате.
Заключение
В данной работе были рассмотрены основные понятия теории графов, их виды. Большое внимание уделили вопросу существования в них эйлеровых цепей и циклов, рассмотрели ряд теорем и свойств. Описали алгоритм нахождения эйлерова цикла в произвольном графе, а в практической части показали его применение на конкретных примерах.
Известно, что эйлеровы графы получили широкое распространение и популярность благодаря тому, что многие головоломки и задачи можно решить с использованием знаний теории графов. Частные примеры таких головоломок и сюжетных задач были приведены в практической части. Задачи на отыскание путей через лабиринты, близкие к задачам на эйлеровы графы, находят применение в современной психологии и при конструировании вычислительных машин. Также с практической точки зрения, сейчас графы применяют во многих других областях науки таких как: программирование, физика, химия, биология, экономика и т.д.
Литература
1. Андерсон, Джеймс А. Дискретная математика и комбинаторика: пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 960с.
2. Березина Л. Ю. Графы и их применение. – М.: Просвещение, 1979.
3. Новиков С.А. Дискретная математика для программистов – СПб.: Питер, 2001. – 304с.
4. Оре о. Графы и их применение. – М.: Мир,1973.
5. Уилсон Р. Введение в теорию графов. – М.: Мир, 1977.
6. Харари Ф. Теория графов. – М.: Мир, 1973.
