Определение смысла естественного языка - это чрезвычайно сложная проблема, которая продолжает оставаться темой интенсивных исследований. Окончательное решение проблемы формализации всего синтаксиса и семантики языка, подобного английскому, далеко еще не найдено. Но (относительно) простые подмножества естественных языков были успешно формализованы, а затем реализованы в виде действующих программ.
При определении смысла языка необходимо в первую очередь найти ответ на вопрос о том, каким образом должен быть представлен смысл. Безусловно, существует много разных вариантов решения этой задачи, и наиболее приемлемый вариант зависит от конкретного приложения. Поэтому возникает не менее важный вопрос — для
Глава 21. Обработка лингвистической информации с помощью грамматических правил 521
чего может использоваться смысл, извлеченный из текста на естественном языке? Типичной областью его применения является доступ с помощью естественного языка к базе данных. В эту область входит поиск ответов на вопросы, сформулированные на естественном языке, касающиеся информации в базе данных, а также обновление базы данных путем ввода новой информации, которая извлечена из входных данных, сформулированных на естественном языке. В таком случае целевым представлением для процесса извлечения смысла должен быть язык операторов запроса и обновления базы данных.
Общепризнано, что для представления смысла фраз на естественном языке хорошо подходят логические высказывания. В целом язык логики является более мощным по сравнению с формальными языками доступа к базе данных; он фактически не только охватывает любые формальные языки доступа к базе данных, но и позволяет учитывать более тонкие семантические закономерности. В данном разделе будет показано, каким образом могут быть сформированы варианты интерпретации простых фраз естественного языка на языке логики с помощью системы обозначений DCG. Эти логические интерпретации будут представлены в виде термов Prolog. Здесь рассматриваются только некоторые интересные идеи, поэтому многие дополнительные сведения, необходимые для более общего описания, будут опущены. Более полное описание данной темы выходит за рамки настоящей книги.
Для начала удобнее всего рассмотреть некоторые фразы и конструкции естественного языка и попытаться выразить их смысл в форме логических высказываний. Вначале рассмотрим фразу "John paints" (Джон рисует). Наиболее приемлемый способ представления смысла этой фразы в форме логического высказывания (в виде терма Prolog) состоит в следующем: paints(john)
Обратите внимание на то, что в данном случае глагол "рисует" является непереходным, поэтому соответствующий предикат paints имеет только один параметр.
Следующим примером фразы является "John likes Annie" {Джон любит Энни). Формализованное выражение смысла этой фразы может состоять в следующем: likes (john, annie)
Глагол "любит" является переходным, и в соответствии с этим предикат likes имеет два параметра. Теперь попытаемся определить смысл подобных простых фраз с помощью правил DCG. Прежде всего начнем исключительно с синтаксиса, а затем будем постепенно вводить в эти правила смысловые интерпретации. Ниже приведена грамматика, которая позволяет легко охватить синтаксис этих фраз, рассматриваемых в качестве примера.
sentence --> noun_phrase, verb_phrase. % Фраза состоит из именной •
* и глагольной конструкции
noun phra3e -> proper noun. % Имя собственное
verb _ phrase -> intrans verb. % Непереходный глагол:
verb_phxase --> trans_verb, noun_phrase, % Переходный глагол
intransverb --> [ paints]. trans verb --> [ likes]. propernoun -- > [ john]. propernoun --> [ annie).
Теперь введем в эти правила смысл. Начнем с более простых категорий (с существительного и глагола), а затем перейдем к более сложным грамматическим категориям. Приведенные выше примеры показывают, что требуется ввести следующие определения. Во-первых, необходимо определить смысл имени собственного. В данном случае смысл имени собственного john - это просто john: proper_noun (john) --> [ john].
Во-вторых, необходимо определить смысл непереходного глагола, такого как глагол "рисует". Эта задача немного сложнее. Предикат с обозначением смысла этого глагола молено представить следующим образом: paints(X)
522 Часть II, Применение языка Prolog в области искусственного интеллекта
где X — переменная, значение которой становится известным только из контекста, иными словами, из именной конструкции. В соответствии с этим правило DCG для предиката paints состоит в следующем: intrans_verb{ paints(X)) --> [ paints].
Теперь рассмотрим такой вопрос: как сформировать из этих двух смысловых значений, john и paints { X), требуемый смысл всей фразы paints (john)? Для этого необходимо обеспечить, чтобы параметр X предиката paints стал равным john.
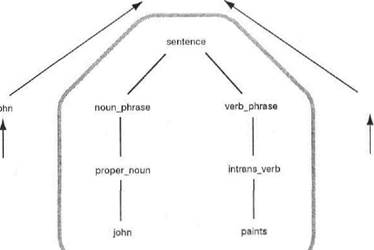
На данном этапе целесообразно проанализировать применяемые операции с помощью графической схемы, как показано на рис. 21.5. На этом рисунке показано, как смысл отдельных конструкций фразы преобразуется в смысл всей фразы. Для достижения эффекта распространения семантических (смысловых) значений конструкций фразы можно определить, что предикаты noun_phrase и verb_phrase получают свои семантические значения из предикатов propernoun и intransverb, как показано ниже,
palnts(jolin>
|
| paints! X) |
| paliils(X) |
| John |
Рис. 21.5. Дерево синтаксическою анализа фразы "John paints", в кото-роя показано, какое смысловое значение соответствует каждому из узлов. Логический смысл каждой конструкции фразы закреплен за соответствующим, нетерминальным узлом в дереве. Стрелки показывают, каким образом накапливаются смысловые значения конструкций
Остается определить смысл всей фразы. Ниже показаны результаты первой попытки решения этой задачн. sentence; S) -> noun_phrase{ HP), verb_phrase(V?), {compose(NP, VP, S)}.
В соответствии с первоначальным замыслом цель compose! NP, VP, 3) должна была аккумулировать смысловые значения именной конструкции john и глагольной конструкции paints [ X), Введем такое понятие, что X — является деятелем в предикате paints { X), и определим следующее отношение: actor(VP, Actor)
Глава 21. Обработка лингвистической информации с помощью грамматических правил 523
В этом отношении Actor — это деятель в смысловом значении глагольной конструкции VP. В таком случае одно из предложений процедуры actor принимает следующий вид:
actor! paints(X), X).
После определения отношения actor появляется возможность создать композицию смысловых значений именной и глагольной конструкций следующим образом:
compose(NP, VP, VP):- % Смысловым значением фразы является VP, где
actor(VP, NP). % деятелем ас^ог в конструкции VP служит NP
Очевидно, что первая попытка определения смысла всей фразы оказалась удачной, но можно найти более удобный метод. Мы сможем избежать необходимости введения дополнительных предикатов compose и actor, если сделаем параметр Х в терме paints [ X) "видимым" вне терма, чтобы он стал доступным для конкретизации. Этой цели можно достичь, переопределив смысловые значения предикатов verb_phrase и intrans_verb таким образом, чтобы X стал дополнительным параметром, как показано ниже.
intrans verb(Actor, paints{ Actor)) --> [ paints]. verb_phrase[ Actor, VP) -> intrans^verb(Actor, VP).
Благодаря этому параметр Actor становится легко доступным и обеспечивает возможность сформулировать более простое определение смысла фразы следующим образом: sentence! VP) -> noun_phrase(Actor), verb_phrase(Actor, VP).
Эта конструкция вынуждает параметр "деятель" (Actor) смыслового значения глагола стать равным смыслу именной конструкции.
Такой метод обеспечения доступа к частям грамматических конструкций, выражающим смысловые значения, представляет собой один из приемов, часто используемых при включении смысловых значений в правила DCG. По сути, этот метод действует следующим образом. Смысл одной из конструкций фразы определяется в "эскизной" форме, например paints (SorrieActor). Такой предикат определяет общую форму смыслового значения, но оставляет часть этого значения неконкретизи-рованной (в данном случае это — переменная SomeActor). Такая неконкретизиро-ванная переменная служит в качестве слота (своего рода "гнезда"), который может быть заполнен позже с учетом смысловых значений других синтаксических конструкций в данном контексте. Подобное заполнение слотов может осуществляться с помощью операции согласования интерпретатора Prolog. Но для упрощения реализации этой операции слоты необходимо сделать видимыми, добавив их в качестве дополнительных параметров к нетерминальным символам. Введем следующее соглашение, касающееся порядка расположения этих параметров, — в начале должны находиться "видимые слоты" смыслового значения синтаксической конструкции, а за ними должно следовать само смысловое значение; в качестве примера применения такого соглашения можно указать предикат verb_phrase (Actor, VPMeaning).
Этот метод можно также применить к переходным глаголам следующим образом. Смыслом глагола "любит" является likes (Somebody, Something) (кто-то любит что-то), где Sorr.ebody и Something - слоты, которые должны быть видимыми извне. Таким образом, может быть составлено следующее правило: trans_verb(Somebody, Something, likes(Somebody, Something)) -> [ likes].
Глагольная конструкция с переходным глаголом содержит именную конструкцию, которая предоставляет значение для Something, поэтому имеет место такое правило: verb_phrase(Somebody, VP) -->
trar.s_verb(Somebody, Something, VP), noun_phrase (Something). Выше в данном разделе были представлены некоторые основные идеи в области обработки смысловых значений, но приведенные правила DCG позволяют обрабатывать лишь самые простые языковые фразы. А если именные конструкции содержат
524 Часть II. Применение языка Prolog в области искусственного интеллекта
такие определяющие слова, как "а" {неопределенный артикль) и "every" (местоимение "каждый"), то способы выражения смысла становятся гораздо более сложными. Эта тема рассматривается в следующем разделе.
21.3.2. Смысл определяющих слов "а" и "every"
Обработка фраз, содержащих такие определяющие слова, как "а", становится намного более сложной по сравнению с фразами, которые описаны в предыдущем разделе. В качестае примера рассмотрим такую фразу: "A man paints" (Некий мужчина рисует). Было бы большой ошибкой считать, что эта фраза имеет смысл paints (man), поскольку в ней фактически сказано: "Существует некий мужчина, который рисует", а не "Мужчинам свойственно рисовать". В форме логического высказывания эта фраза может быть представлена следующим образом: Существует X, такой, что X - мужчина и X рисует.
Переменную X, представленную в составе такого логического высказывания, принято называть переменной, к которой применяется квантор существования (в виде глагола "существует"). Примем за основу способ представления переменных, определяемых таким образом, с помощью следующего терма Prolog: exists! x, man(X) and paints! X)}
Первым параметром этого терма является переменная X, которая подлежит определению с помощью квантора существования, а оператор and. считается объявленным как инфиксный оператор следующим образом::- ор(100, xfyr and>.
Хотя на первый взгляд это может показаться неожиданным, но синтаксическим объектом, который диктует необходимость применения такой сложной логической интерпретации, является определяющее слово "а". Поэтому слово "а" в определенном смысле доминирует над всей этой фразой. Чтобы лучше понять, каким образом формируется это смысловое значение, рассмотрим именную конструкцию "a man". Она имеет следующий смысл: Существует неки'л X, такой, что X - мужчина.
Но во фразах, где появляется именная конструкция "a man", таких как "a man paints", мы всегда стремимся сообщить об этом мужчине что-то еще (в данном случае • — не только то, что ом существует, но и что он рисует). Поэтому наиболее подходящая форма для выражения смысла именной конструкции "a man" состоит в следующем: exists! X, man! X) and Assertion!
где Assertion — некоторое утверждение об X. Такое утверждение, касающееся X, зависит от контекста, т.е. от глагольной конструкции, которая следует за именной конструкцией "a man". Переменная Assertion конкретизируется только после того, как становится известен контекст, в котором она появляется.
Аналогичный ход рассуждений позволяет найти правильную формулировку смысла определяющего слова "а". Это определяющее слово показывает следующее:
Существует некий X, такой, что
X обладает некоторьзл свойством ( например, man (X)) и является истинным еще какое-то утверждение, касающееся X (например, paints(X)).
Эта формулировка может быть представлена в виде терма Prolog таким образом: exists! X, Property and Assertion)
Обе переменные, Property и Assertion, представляют собой слоты для смысловых значений, извлекаемых из контекста и помещаемых в эти слоты. Для упрощения переноса смысловых значений из других синтаксических конструкций в контексте можно сделать видимыми некоторые части смысловых значений определяющего
Глава 21. Обработка лингвистической информации с помощью грамматических правил 525
слова "а", как описано в предыдущем разделе. Подходящее правило DCG для определяющего слова "а" приведено ниже. determiner[ X, Prop, Assn, exists (X, Prop and Assn)1 --> [ a].
Логический смысл крошечного определяющего слова "а" оказался на удивление сложным. Еще одно определяющее слово, "every", можно проанализировать аналогичным образом. Рассмотрим фразу "Every woman dances" (Каждая женщина танцует). Логическая интерпретация этой фразы приведена ниже. Для всех X, если X — же.чщинаг то X танцует.
Эта формулировка может быть представлена с помощью следующего терма Prolog: all I Xr woman(X) -> dances{ XI)
где "=>" - инфиксный оператор, обозначающий логическую импликацию. Таким образом, определяющее слово "every" указывает на наличие смыслового значения, которое имеет такую эскизную структуру: all (X, Property ~> Assertion)
Правило DCG, которое описывает смысл определяющего слова "every" и делает слоты в этой эскизной структуре видимыми, приведено ниже, determiner! X, Prop, Assn, all{ X, Prop -> Assn)) --> [ every].
Теперь, после описания смысловых значений определяющих слов мы можем сосредоточиться иа изучении того, как смысловые значения этих определяющих слов объединяются со смысловыми значениями других синтаксических конструкций в контексте и приводят в конечном итоге к получению смыслового значения всей фразы. Первое представление об этом можно получить, снова вернувшись к рассмотрению фразы "A man paints", которая имеет такой смысл:
exists! X, man[ X) and p a i n t s [ X))
Смысл определяющего слова "а" уже был выявлен следующим образом: exists[ X, Prop and Assn)
После сравнения этих двух смысловых значений сразу же становится очевидно, что основная структура смыслового значения этой фразы продиктована определяющим словом. Смысл всей этой фразы можно скомпоновать, как показано на рис. 21.6; начнем с эскизного смыслового значения, предписанного определяющим словом "а" таким образом: exists (X, Prop and Assn)
Затем переменная Prop становится конкретизированной значением именной конструкции, a Assn — значением глагольной конструкции. Основная структура смыслового значения этой фразы получена из именной конструкции. Обратите внимание на то, что в этом состоит отличие от более простой грамматики, описанной в предыдущем разделе, в которой смысловая структура фразы была продиктована глагольной конструкцией. Снова применяя метод, позволяющий сделать видимыми некоторые части смыслового значения, можно сформулировать отношения между смысловыми значениями, показанными на рис. 21.6, с помощью следующих правил DCG:
sentence! S) -> noun_phrase(X, Assn, S), verb_phrase(X, Assn).
no-un phrase [ X, Assn, S) --> determiner; X, Prop, Assn, S), noun (X, Prop).
verb_phrase(X, Assn) --> intrans_verb(X, Assn).
intrans_verb(X, paints[ X)) --> [ paints].
determiner< X, Prop, Assn, exists! X, Prop and Assn)) -> [ a!.
noun(X, man(X]) --> [ man].
После ввода этой грамматики в интерпретатор Prolog может быть задан вопрос для формирования смысла фразы "А лап paints", как показано ниже.
?- sentence! S, [ a, man, paints), []). Е •= exists! X, man { X) and paints! X))
Здесь ответ системы Prolog немного отредактирован таким образом, что имя переменной наподобие 123, сформированное системой Prolog, заменено на X
526 Часть II. Применение языка Prolog в области искусственного интеллекта
exists) X, man[X) and paints X])

|
| r exists! X. man[ X! and Аээп) |
| sxistsj X, Prop and Assn) delarmliier noun \ manfX] inirons vi-irh |
| paints(X) |
Рис. 21,6. Накопление смысловых значений для определения смысла фразы "A man paints". Общая форма смыслового значения этой фразы продиктована определяющим словом "а". Стрелки показывают направление переноса смысловых значений из одной синтаксической конструкции, е другую
Грамматика, приведенная в предыдущем разделе, позволяет обрабатывать такие фразы, как "John paints". После внесения изменений в эту грамматику необходимо обеспечить, чтобы новый вариант грамматики, позволяющий обрабатывать фразы типа "A man paints", был способен также обрабатывать более простые фразы наподобие "John paints". Для этого требуется включить в новую именную конструкцию средства определения смысла имен собственных. Ниже приведены правила, которые позволяют решить такую задачу. pcoper_noun(John) --> [ John]. noun_phrase (X, Assn., Assnl --> proper_noun j X).
Последнее из этих правил просто указывает, что весь смысл именной конструкции такого рода совпадает со значением второго "видимого слота", т.е. Assn. Значение этого слота может быть получено из контекста (из глагольной конструкции), как при обработке следующего вопроса:
?- sentence(S, [ John, paints], []). S = paints i John)






