Для количественной характеристики различных объектов используется абстракция называемая числом. Число записывается некой системой знаков – цифрами. Системой счисления называют совокупность правил записи чисел.
Различают позиционные и непозиционные системы счисления.
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от ее положения в числе. Классическим примером такой системы счисления является римская, в которой в качестве цифр используются латинские буквы: I обозначает единицу, V – пять, X – десять, L – пятьдесят, C – сто, D – пятьсот, M – тысячу. Натуральные числа записываются при помощи повторения этих цифр, а для получения значения числа необходимо просто просуммировать все входящие в него цифры. Из этого правила есть исключение, из-за которого римская система счисления не является в полной мере непозиционной: когда младшая цифра стоит перед старшей, то ее необходимо вычитать при определении значения числа.
Например:
DLXI = 500 + 50 + 10 + 1 = 561,
CDIX = 500 – 100 + 10 – 1 = 409.
В позиционных системах счисления значение каждой цифры в записи числа зависит от ее позиции в числе. Например, в десятичном числе 111 первая единица означает один, вторая – десять, третья – сто. Количество цифр, которые могут использоваться для представления чисел в данной системе счисления, называется основанием системы счисления и обозначается буквой 
. Место записи цифры в числе называется разрядом числа, которые нумеруются справа налево, начиная с нуля.
Любое число 
в системе счисления с произвольным основанием можно записать состоящим из 
отдельных цифр 
(где индекс означает номер разряда) в следующем виде:
= 
.
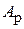Очевидно, что при этом справедливо условие 
.
Также можно представить число таким выражением, которое можно использовать для вычисления значения числа:
= 
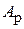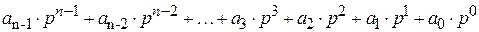. (1.1)
Здесь и далее мы будем рассматривать только целые числа.
