Работа с математическим сопроцессором в среде Assembler
Основные сведения
Сопроцессор - это специализированная интегральная схема, которая работает в содружестве с ЦП, но менее универсальна. Сопроцессор предназначен для выполнения специфического набора функций, например: выполнение операций с вещественными числами - математический сопроцессор, подготовка графических изображений и трехмерных сцен - графический сопроцессор, цифровая обработка сигналов - сигнальный сопроцессор и др.
Один из наиболее распространенных типов сопроцессоров - математический сопроцессор. Математический сопроцессор предназначен для быстрого выполнения арифметических операций с плавающей точкой, предоставления часто используемых вещественных констант (
, log210, log2e, ln2,:), вычисления тригонометрических и прочих трансцендентных функций (tg, arctg, log,...).
Большинство современных математических сопроцессоров для представления вещественных чисел используют стандарт IEEE 754-1985 "IEEE1) Standard for Binary Floating-Point Arithmetics". Старший разряд двоичного представления вещественного числа всегда кодирует знак числа. Остальная часть разбивается на две части: экспоненту и мантиссу. Вещественное число вычисляется как: (-1)S·2E·M, где S - знаковый бит числа, E - экспонента, M - мантисса. Если 1 
M<2, то такое число называется нормализованным. При хранении нормализованных чисел сопроцессор отбрасывает целую часть мантиссы (она всегда 1), сохраняя лишь дробную часть. Экспонента кодируется со сдвигом на половину разрядной сетки, таким образом, удается избежать вопроса о кодировании знака экспоненты. Т.е. при 8-битной разрядности экспоненты код 0 соответствует числу -127, 1 - числу -126,..., 255 числу +126 (экспонента вычисляется как код 127).
Стандарт IEEE-754 определяет три основных способа кодирования (типа) вещественных чисел.
| Таблица 2. Типы (способы кодирования) вещественных чисел | ||
| Тип | Диапазон значений (по модулю) | Двоичное представление |
| вещественное ординарной точности (single precision) - 32 бит | 1,18·10-38... 3,40·1038 |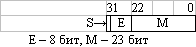 
|
| вещественное двойной точности (double precision) - 64 бит | 2,23·10-308... 1,79·10308 |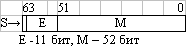 
|
| вещественное расширенной точности (extended precision) - 80 бит | 3,37·10-4932... 1,18·104392 |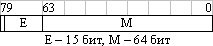 
|
Если результат численной операции не может быть точно представлен в выбранном формате, сопроцессор выполняет округление в соответствии с полем RC (таблица 3). По умолчанию RC = 00.
| Таблица 3. Режимы округления сопроцессоров Intel x87 | |||
| RC | Режим | Пример 1 1,000E21 < 2,23E100 < 1,001E21-1,001E21 < -2,23E100 < -1,000E21 | Пример 2 1,000E21 < 2,05E100 < 1,001E21-1,001E21 < -2,05E100 < -1,000E21 |
| Округление к ближайшему (или четному) | 2,23E100 ≈ 1,001E21-2,23E100 ≈ -1,001E21 | 2,05E100 ≈ 1,000E21-2,05E100 ≈ -1,000E21 | |
| Округление вниз (к ∞) | 2,23E100 ≈ 1,000E21-2,23E100 ≈ -1,001E21 | 2,05E100 ≈ 1,000E21-2,05E100 ≈ -1,001E21 | |
| Округление вверх (к +∞) | 2,23E100 ≈ 1,001E21-2,23E100 ≈ -1,000E21 | 2,05E100 ≈ 1,001E21-2,05E100 ≈ -1,000E21 | |
| Округление к нулю (усечение) | 2,23E100 ≈ 1,000E21-2,23E100 ≈ -1,000E21 | 2,05E100 ≈ 1,000E21-2,05E100 ≈ -1,000E21 |
