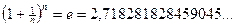ЗАНЯТИЕ № 1
Предел последовательности.
Необходимые сведения.
1.Понятие предела числовой последовательности. Число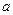 
называют пределом последовательности 
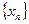, если для каждого 
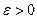существует такое натуральное 
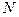, что для любого 
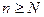верно неравенство: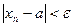 
или короче: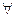 
: 
: .
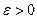
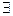
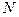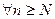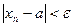Обозначают: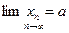 
. Говорят: последовательность сходится к .
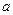Последовательность, сходящуюся к нулю, называют бесконечно малой.
2.Последоваетельность называют расходящейся, если никакое конечное число не является её пределом
или короче: :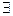 
: 
.
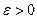
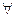
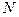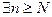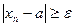3. Свойства последовательностей
· Если последовательность имеет предел, то она ограниченна.
· Если последовательность неограниченна, то она расходится.
· Если последовательность 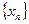бесконечно малая, а последовательность 
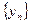ограниченная, то последовательность 
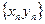бесконечно малая.
· Вспомните арифметические свойства пределов (предел суммы и т.п.)
4.Для того чтобы число 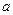было пределом последовательности 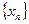необходимо и достаточно, чтобы для всех 
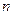выполнялось 
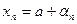, где 
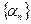- бесконечно малая последовательность.
5.Есл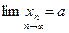и 
и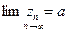 
, и для всех 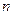, начиная с некоторого, 
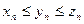, то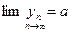 
. (Правило двух милиционеров)
6.Последовательность называется бесконечно большой, если для каждого 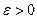существует такое натуральное 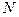, что для любого 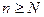верно неравенство: 
.
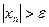Обозначают: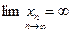 
. Говорят: последовательность имеет бесконечный предел.
Всякая бесконечная последовательность является неограниченной и расходящейся.
7. Теорема Вейерштрасса. Ограниченная и монотонная (начиная с некоторого номера) последовательность имеет конечный предел.
Важный пример такой последовательности: 
