Лабораторная работа № 4
Исследование трехфазной цепи при соединении приемников треугольником
Цель работы
Опытное и аналитическое исследование различных режимов трехфазной электрической цепи при соединении приемников треугольником.
Пояснения к лабораторному стенду
Работа выполняется на универсальном стенде. Перед выполнением работы необходимо с помощью перемычек собрать схему (рис. 1).
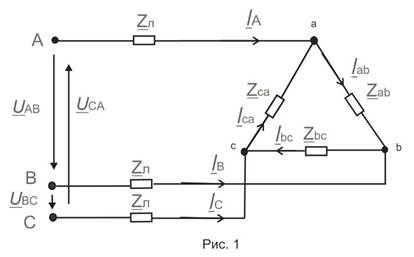
Основные теоретические положения
При соединении приемника треугольником расчет симметричной и несимметричной трехфазной цепи с учетом сопротивлений линейных проводов обычно выполняется путем преобразованием треугольника в эквивалентную звезду по формулам
; 
; 
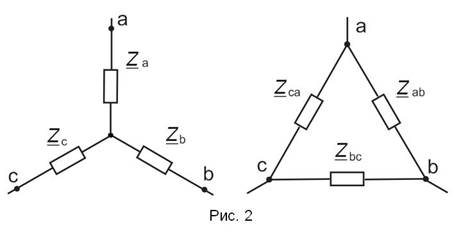
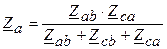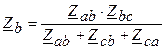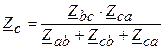(1)
После преобразования задача сводится к расчету симметричной или несимметричной трехфазной цепи с приемником, соединенным звездой без нулевого провода. Решение такой задачи рассмотрено в предыдущей лабораторной работе.
Определив фазные напряжения в эквивалентной звезде методом, приведенным в предыдущей работе, можно найти линейные напряжения на приемнике:
; 
; 
.
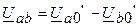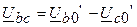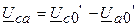По закону Ома токи в фазах треугольника
; 
; 
.
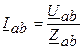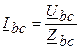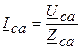В аварийных режимах при обрыве фазы приемника или линейного провода расчеты упрощаются.
При обрыве фазы приемника (рис.3)
; 
; 
;
; 
; 
;
; 
; 
.
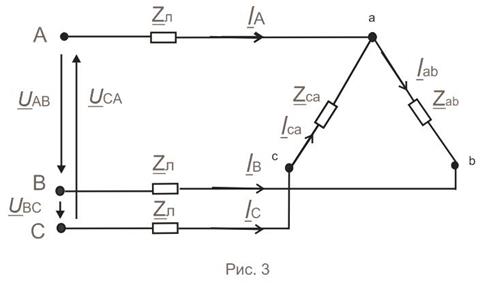
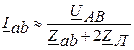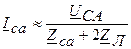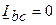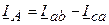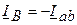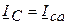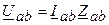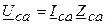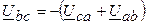В случае обрыва линейного провода получаем
; 
;
; ; 
;
; .
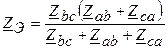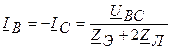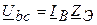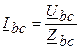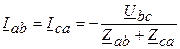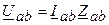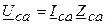Построение диаграммы начинается с построения на комплексной плоскости векторов фазных токов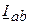 
, 
, 
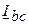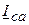. Затем, соединив их концы, строим векторы линейных токов.
Для построения диаграмм напряжений строим векторы фазных напряжений приемника, учитывая сдвиги фаз между соответствующими напряжениями и токами. Получаем замкнутый треугольник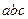 
. Зная направления векторов линейных токов 
, 
, 
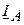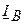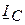, из вершин полученного треугольника строим векторы падений напряжений в линейных проводах. Концы построенных векторов будут соответствовать точкам A, B, C источника. Соединив эти точки на диаграмме, получим векторы линейных напряжений, приложенных к схеме.
Пример диаграммы цепи с активными сопротивлениями линейных проводов и приемника показан на рис. 4.
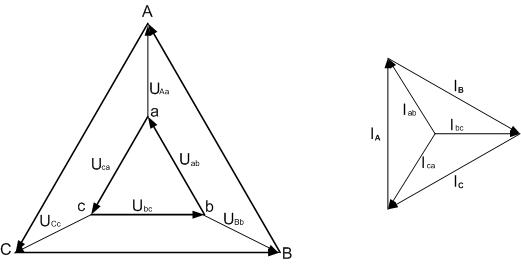
Рис.4
