1. Множество всех первообразных функции 
имеет вид…
2. Укажите все верные утверждения (С – произвольная постоянная)
1) 
;
2) 
;
3) 
;
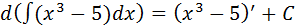4) 
.
3. В неопределенном интеграле 
подынтегральная функция разлагается на элементарные дроби
; 
; 
; 
.
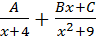4. В неопределенном интеграле 
введена новая переменная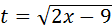 
. Тогда интеграл примет вид:
5. Множество первообразных функции 
равно
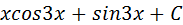
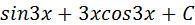
6. Если функция 
непрерывна на отрезке 
и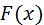 
– какая-либо её первообразная на , то интеграл 
равен:
; 
; 
; 
.
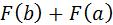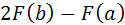7. Определенный интеграл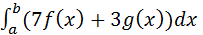 
может быть равен:
; 
;
; 
.
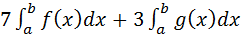8. В определенном интеграле 
введена новая переменная 
. Тогда интеграл примет вид:
; ; ; 
.
9. Определенный интеграл 
равен…
10. Если 
; 
, то интеграл 
равен…
11. Определенный интеграл, выражающий площадь треугольника с вершинами (0;0); (2;0); (2;6), имеет вид:
; 
; 
; 
.
12. Площадь фигуры, изображенной на рисунке,
Равна:
8 5 7 6
13. Несобственный интеграл 
равен …..
14. Для функции 
справедливы соотношения:
; 
; 
; 
.
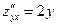15. Для функции 
справедливы соотношения:
; 
; 
; 
; 
.
16. Для стационарных точек функции 
справедливы
утверждения:
их число равно 3; их число равно 2; их число равно 1.
17. Для функции 
, имеющей две стационарные точки М 
(-1,0) и М 
(1,0), справедливо утверждение:
-её экстремальное значение равно 0;
- М (-1,0) и М (1,0) – точки максимума;
-М (-1,0) и М (1,0) – точки минимума;
-точек экстремума нет.
18. Модуль градиента функции 
в точке М (2,1) равен…
19. Производная функции 
в точке М (1,2) в направлении, идущем от этой точки к точке Р(4,6), равна…
20. Уравнение нормали к поверхности 
в точке М (3,1,4) имеет вид:
; 
; 
; 
.
21. Интеграл 
где 
; 
; 
равен ….
22. Двойной интеграл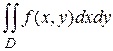 
где 
область ограниченная линиями 
, 
, 
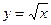равен:
; 
; 
; 
.
23. Если в двойном интеграле 
изменить порядок интегрирования, то интеграл примет вид:
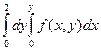
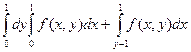
24. Линиями уровня функции 
являются
1) параболы, 2) окружности, 3) гиперболы, 4)прямые, 5)эллипсы.
25. Частной производной функции 
по переменной у в точке 
называется
1) 
2) 
3) 
4) 
