Вторая методика обработки результатов измерений применяется в случае, когда невозможно осуществить серию равноточных измерений. Возможно также ее применение вместо вышеизложенной методики (назовем ее первой методикой).
Суть второй методики состоит в том, что для каждого значения прямого измерения вычисляется собственное значение косвенного измерения. В результате получается последовательность близких по величине n чисел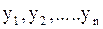 
. За наиболее вероятное значение косвенного измерения принимается его среднее арифметическое значение: 
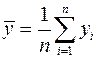(21)
Затем для заданной величины доверительной вероятности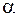 
определяется коэффициент Стьюдента 
и вычисляется квадрат случайной погрешности косвенного измерения:
(22)
Систематическую (приборную) погрешность косвенного измерения определяют по формулам погрешностей (см. формулы 14, 15, 16). При этом используют результаты «наилучшего» опыта. Под «наилучшим» опытом мы понимаем тот, для которого результат косвенного измерения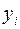 
оказался ближе всего к среднему значению косвенных измерений 
.
Наконец, определяют полную погрешность косвенного измерения по формуле, аналогичной формуле (6):
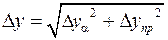. (22)
Результат, как и в первой методике, записывают с указанием доверительного интервала и вероятности.
