Функция:

| Ввод x,y, epsilon |
| abs(y-x)>epsilon |
| Начало |
| z=x-(y-x)*f(x)/(f(y)-f(x)), x=y, y=z |
| Вывод результата Z |
| конец |
// Hords.cpp: Defines the entry point for the console application.
//
#include "stdafx.h"
#include <math.h>
#include <stdio.h>
double f (double x);
FILE *tabfun1;
int main(void)
{
double a,b,c,eps;
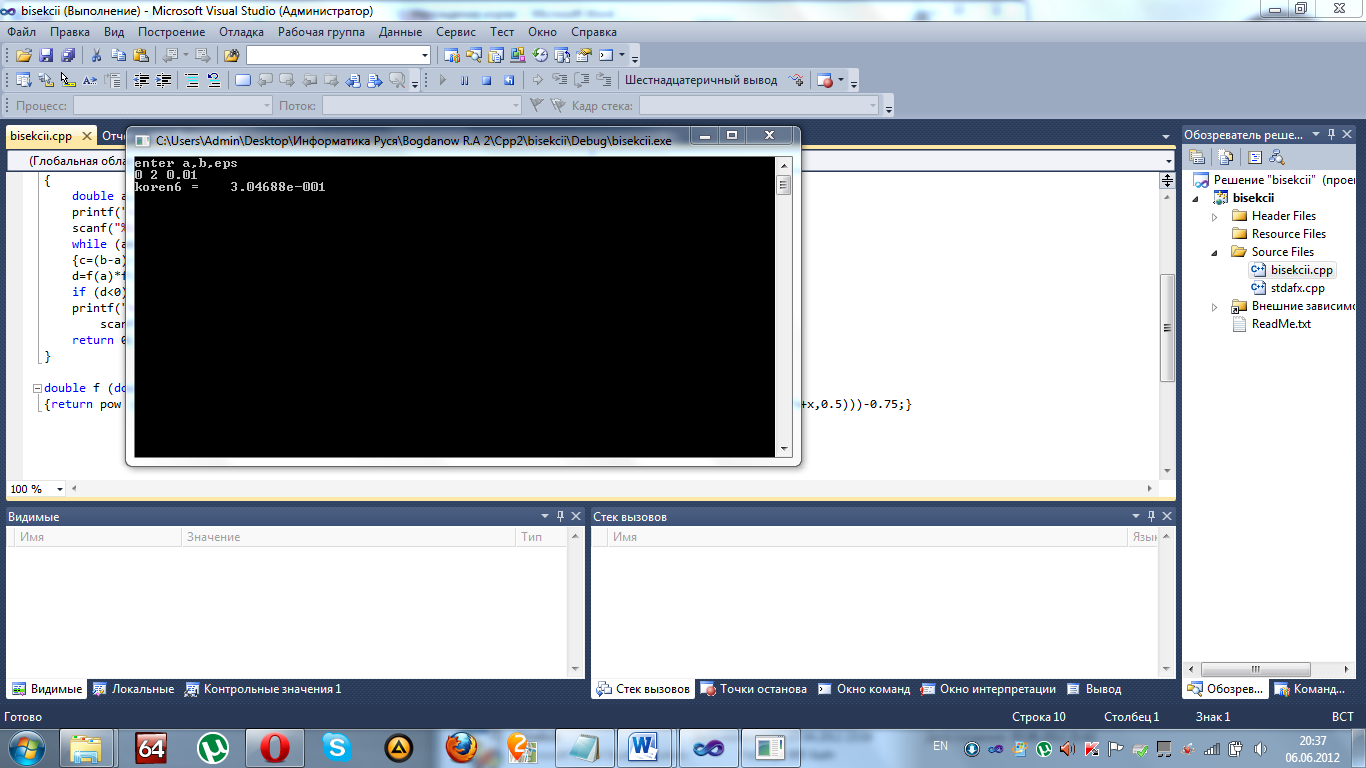
printf("enter a,b,eps \n");
scanf("%le%le%le",&a,&b,&eps);
while (abs(a-b)>eps)
{c=a-(b-a)*f(a)/(f(b)-f(a));
b=a; a=c; }
printf("koren6 = %15.5le",c);
tabfun1=fopen("a1.dat","w");
fprintf(tabfun1,"%15.5le %15.5le\n",'a=',a,' b=',b,' ','eps=',eps);
fclose(tabfun1);
scanf("%le", &a);
return 0;
}
double f (double x)
{return pow(pow(exp(x)+exp(-x),0.5)+pow(exp(2*x)+exp(-2*x),0.5),1/exp(x))/(sin(x)+cos(2*x)+exp(pow(x*x+x,0.5)))-0.75;}
}
Вывод: При вычислении корня методом хорд на промежутке между 0 и 2 получено значение 2.1
Нахождение корня в MatLab:
Задание 1: Вычислить корень функции:
f=((sqrt(exp(x)+exp(x))+sqrt(exp(2.*x)+exp(2.*x)).^(1/exp(x)))/sin(x)+cos(2.*x)+exp(sqrt(x.^(2)+x)))-0.75
Программный код:
function MethodHord
a=0
b=2
eps=1.*10^(-6)
while ((b-a)>eps)
c=(a+b)./2;
d=func(a).*func(c);
if (d>0) a=c;
else b=c;
end
end
x=(a+b)./2;
x
end
function f = func(x);
f=((sqrt(exp(x)+exp(x))+sqrt(exp(2.*x)+exp(-2.*x)).^(1/exp(x)))/sin(x)+cos(2.*x)+exp(sqrt(x.^(2)+x)))-0.75;
end
Результат:
a =
b =
eps =
1.0000e-006
x =
2.0000






